2596. 检查骑士巡视方案
骑士在一张
n x n的棋盘上巡视。在 有效 的巡视方案中,骑士会从棋盘的 左上角 出发,并且访问棋盘上的每个格子 恰好一次 。给你一个
n x n的整数矩阵grid,由范围[0, n * n - 1]内的不同整数组成,其中grid[row][col]表示单元格(row, col)是骑士访问的第grid[row][col]个单元格。骑士的行动是从下标 0 开始的。如果
grid表示了骑士的有效巡视方案,返回true;否则返回false。注意,骑士行动时可以垂直移动两个格子且水平移动一个格子,或水平移动两个格子且垂直移动一个格子。下图展示了骑士从某个格子出发可能的八种行动路线。
示例 1:
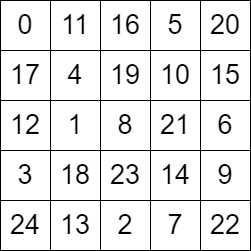
输入:grid = [[0,11,16,5,20],[17,4,19,10,15],[12,1,8,21,6],[3,18,23,14,9],[24,13,2,7,22]] 输出:true 解释:grid 如上图所示,可以证明这是一个有效的巡视方案。示例 2:
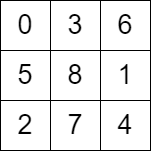
输入:grid = [[0,3,6],[5,8,1],[2,7,4]] 输出:false 解释:grid 如上图所示,考虑到骑士第 7 次行动后的位置,第 8 次行动是无效的。提示:
n == grid.length == grid[i].length3 <= n <= 70 <= grid[row][col] < n * ngrid中的所有整数 互不相同
思路:
初始为x,y 每一次移动后是一个x1 y1 |(x1-x)*(y1-y)| 一定为2,所以就出来了
用表示1的位置与0的位置此方法进行计算 然后2对应的x2 y2索引与1.......全部满足就返回true
但是0 到1到2...的数字位置不知道,所以这时候用一个容器进行排序。具体看题解
class Solution {
public:bool checkValidGrid(vector<vector<int>>& grid) {if(grid[0][0]!=0) //如果骑士不在(0,0)的位置返回false{return false;}int n=grid.size();vector<array<int,2>> arr(n*n);//定义一个n*n的容器 其中每个元素都是长度为2的数组for(int i=0;i<n;i++){for(int j=0;j<n;j++){arr[grid[i][j]]={i,j}; //将0到n*n的对应的索引放在容器中。}} for(int i=1;i<n*n;i++){if(abs(arr[i][0]-arr[i-1][0])*abs(arr[i][1]-arr[i-1][1])!=2) //因为开始的位置与移动 //后的位置一定是 一个1*2的长方形对角 //绝对值的差值为2return false;} return true;}
};