目录
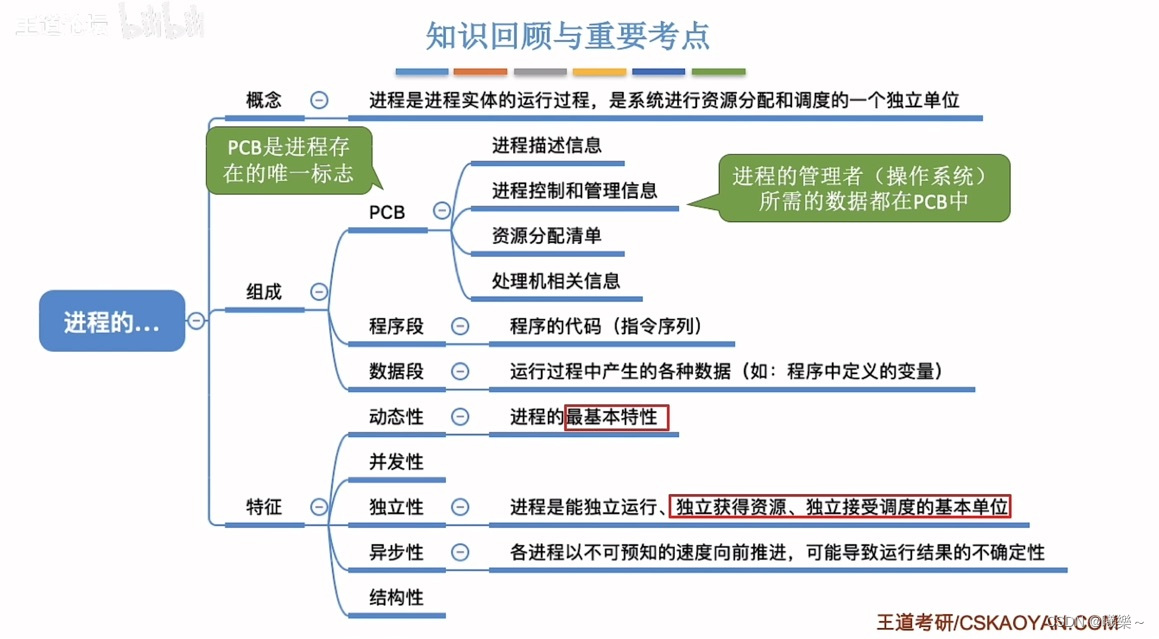
无穷区间上的反常积分
无界函数的反常积分
反常积分的敛散性
反常积分的计算
无穷区间上的反常积分
无穷区间上的反常积分(improper integral on infinite interval)是一种反常积分
设函数f(x)在(a,+∞)上有定义,且f(x)在任意有限区间(a,A)(A>a)上可积,若limA→+∞∫aAf(x)dx存在,则称此极限值为函数f(x)在无穷区间(a,+∞)上的反常积分,记为∫a+∞f(x)dx,即∫a+∞f(x)dx=limA→+∞∫aAf(x)dx.
若函数f(x)在(−∞,b)上有定义,且f(x)在任意有限区间(A,b)(A<b)上可积,若limA→−∞∫Abf(x)dx存在,则称此极限值为函数f(x)在无穷区间(−∞,b)上的反常积分,记为∫−∞bf(x)dx,即∫−∞bf(x)dx=limA→−∞∫Abf(x)dx.
若函数f(x)在(−∞,+∞)上有定义,且∫−∞+∞f(x)dx=∫−∞af(x)dx+∫a+∞f(x)dx均存在,则称此极限值为函数f(x)在无穷区间(−∞,+∞)上的反常积分,记为∫−∞+∞f(x)dx,即∫−∞+∞f(x)dx=∫−∞af(x)dx+∫a+∞f(x)dx.
无界函数的反常积分
如果函数f(x)在区间(a,b)上可积,但在区间端点a或b的任意邻域内无界,则称f(x)在区间(a,b)上无界.这时,如果limx→a+∫xbf(t)dt或limx→b−∫axf(t)dt存在,则反常积分∫abf(x)dx称为收敛的,否则称为发散的.
反常积分的敛散性
反常积分是一种特殊类型的积分,它们涉及到无穷大或无穷小的限制情况。反常积分可以分为两类:无穷限的反常积分和间断点附近的反常积分。它们的敛散性取决于积分的被积函数在积分区间内的性质。
1. 无穷限的反常积分:
- 如果一个无穷限的反常积分在积分区间内收敛,那么它的值是有限的。这意味着积分的结果存在并且不会趋向于无穷大或无穷小。
- 如果一个无穷限的反常积分在积分区间内发散,那么它的值将趋向于无穷大或无穷小。这意味着积分的结果无限增大或无限减小。
2. 间断点附近的反常积分:
- 如果一个反常积分包括一个间断点(例如,被积函数在某一点不连续),则该积分的敛散性取决于该间断点的性质。如果间断点是可去奇点(例如,一个可去的无穷大间断点),则积分通常是有限的,即敛散性为敛散。如果间断点是不可去奇点(例如,一个极限不存在的间断点),则积分通常是无限的,即敛散性为发散。
判断反常积分的敛散性通常需要进行详细的数学分析,包括计算极限或使用收敛定理。一些常见的测试方法包括比较测试、极限比较测试、积分测试等。这些方法可用于确定反常积分是否收敛或发散,以及它们的值是有限的还是无限的。

反常积分的计算
计算反常积分通常涉及到对无穷限或间断点附近的积分进行分析和求解。下面我将简要介绍一些常见情况下的计算方法:
1. 无穷限的反常积分:
a. 上无穷限的反常积分: 如果你要计算形如 ∫(from a to +∞) f(x) dx 的积分,其中 a 可以是任意实数,通常的方法是使用极限来计算。首先,你需要计算极限 lim(x->+∞) ∫(from a to x) f(x) dx。如果这个极限存在且是有限的,那么原积分收敛,其值等于这个极限。
b. 下无穷限的反常积分: 类似地,如果你要计算形如 ∫(from -∞ to b) f(x) dx 的积分,其中 b 可以是任意实数,你需要计算极限 lim(x->-∞) ∫(from x to b) f(x) dx。如果这个极限存在且是有限的,那么原积分收敛,其值等于这个极限。
2. 间断点附近的反常积分:
a. 可去奇点附近的反常积分: 如果被积函数在间断点附近有一个可去奇点,通常可以通过将该奇点修补成连续函数来计算积分。这通常涉及到将间断点处的函数值修正为使之连续,并计算修正后的积分。
b. 不可去奇点附近的反常积分: 如果被积函数在间断点附近有一个不可去奇点,通常需要使用复数分析的方法来计算积分。这可能涉及到使用留数定理等技巧来计算积分的值。
需要注意的是,反常积分的计算可能相当复杂,具体的方法取决于被积函数的性质以及积分区间的特点。在实际计算中,常常需要使用数学软件或符号计算工具来辅助进行计算,特别是对于复杂的积分。