一、实验名称:数列与级数
二、实验环境:Mathematica 10.3软件
三、实验目的:本实验通过Mathematica 10.3软件编程演示Fibonacci数列、调和级数的函数图像及函数关系式,通过Mathematica 10.3软件发现数列与极限状态的性质,体会数列与级数在理论与实际应用中的差距
四、实验内容和步骤以及结果分析
实验一:画Fibonacci数列折线图的函数
1、实验内容:分别取n=20、100、500、1000,观察Fibonacci数列折线图,Fibonacci数列是否调?它是否趋于无穷?它增加的速度是快还是慢?
2、实验步骤:在软件中输入程序如下:

3、实验结果:



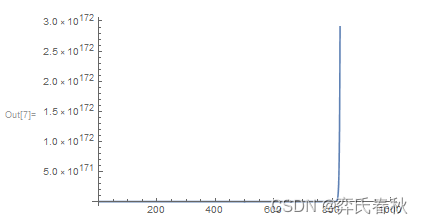
4、结果分析:从实验四个图像可以看出,Fibonacci数列单调递增而且趋于无穷大,n的值越大,图像越陡峭,即递增越快。
实验二:研究点列
1、实验内容:研究数列的极限状态的规律。
2、实验步骤及实验结果:在软件中输入程序如下,运行后得到如下结果:

3、结果分析:根据运行出来的图像可得点列的分布呈网状结构,数列
没有极限。
实验三:用直线去拟合
1、实验内容:分别取n=2000、5000、9000,用直线拟合数据,由此求数列的近似表示。注意观察
的线性项的系数,它与黄金分割率的联系是什么?
2、实验程序:

3、实验结果:

4、结果分析:从实验结果可以看出,当取的n的值越大,线性拟合的结果越趋于稳定,而且的线性项的系数与黄金分割率的和近似等于1。
![]()
2、实验步骤:输入程序如下:
![]()
3、实验结果:
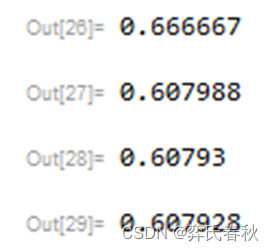
4、结果分析:对取不同的值,该级数的部分积结果误差比较大,当
越大时,结果的误差越小,即结果越精确。