文章目录
- 一、背景
- 二、Improved DDPM——提升 Log-likelihood
- 2.1 可学习的方差
- 2.2 改进 noise schedule
- 2.3 降低梯度噪声
- 三、效果
论文:Improved Denoising Diffusion Probabilistic Models
代码:https://link.zhihu.com/?target=https%3A//github.com/openai/improved-diffusion
时间:2021.02.18
Improved DDPM 贡献:
- 学习方差会让生成效果更好(DDPM 中只学习了均值,方差是一个常数)
- 提出了余弦加噪方法,比线性加噪效果更好
一、背景
首先回顾一下 DDPM
前向传播过程:
-
通过给输入 x 0 x_0 x0 进行 t t t 次加噪 β t ∈ ( 0 , 1 ) \beta_t \in (0,1) βt∈(0,1),得到最终的 x t x_t xt
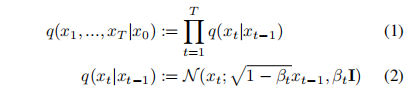
-
假设给定一个足够大的 T T T 和一个变化规则良好的 β t \beta_t βt,则 x T x_T xT 就近似一个各向同性高斯分布。
-
假设已知 q ( x t − 1 ∣ x t ) q(x_{t-1}|x_t) q(xt−1∣xt),就是能直接从 x t x_t xt 推出 x t − 1 x_{t-1} xt−1,那么就能一路反推得到 q ( x 0 ) q(x_0) q(x0),从而采样出 x 0 x_0 x0,但是没有办法直接推出来,所以只能使用神经网络来估计出来每次反推的结果:
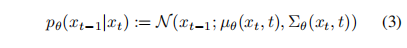
-
将 q 和 p 结合起来就是一个变分自编码器,可将变分下界(variational lower bound, VLB)写成如下形式:
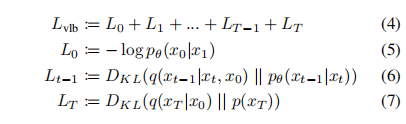
-
公式 4 中,除了 L0 以外,其他每项都是两个高斯分布的 KL 散度
-
从 x 0 x_0 x0 可以直接得到 x t x_t xt,且边界分布如下,噪声的系数是方差,可以用这个系数来描述噪声的 schedule
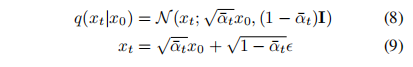
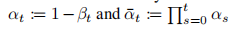
-
基于贝叶斯理论,可以计算后验分布如下:
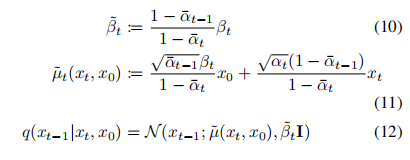
实际训练过程:
-
目标函数 4 是多个独立项之和,每一项 L t − 1 L_{t-1} Lt−1 基本都是真实噪声和预测噪声的 KL 散度
-
怎么预测噪声均值 μ θ \mu_{\theta} μθ 呢,之前的方法大都是直接使用神经网络来预测,还有一种方法是通过预测 x 0 x_0 x0,然后基于公式 11 来预测。此外,还能通过使用公式 9 和 11 来得到:
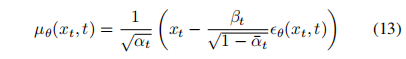
-
DDPM 中发现预测噪声能做的比较好,尤其是使用 reweighted loss 函数,下面的函数 14 可以看做从公式 4 中重加权得到的,且发现直接优化下面的公式 14 比优化 4 更好:
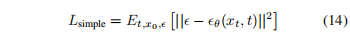
二、Improved DDPM——提升 Log-likelihood
尽管 DDPM 在 FID 和 Inception Score 上获得很很好的效果,但在 Log-likelihood 上没有得到很高的得分
Log-likelihood 也是生成式任务上一个很重要的衡量指标,一般认为优化 Log-likelihood 能够让生成式模型捕捉数据分布的整体信息,所以,探索 DDPM 为什么在 Log-likelihood 上表现的不好还是很重要的
其理论出处文中给的是 VQ-VAE2:

2.1 可学习的方差
DDPM 在优化 L s a m p l e L_{sample} Lsample 的时候,设置的固定的方差 σ t 2 I \sigma_t^2I σt2I,方差是没有学习的,当 σ t 2 = β t \sigma_t^2=\beta_t σt2=βt 或 σ t 2 = β ˜ t \sigma_t^2=\~{\beta}_t σt2=β˜t 时,采样质量没什么差别。
所以 DDPM 设置的 σ t 2 = β t \sigma_t^2=\beta_t σt2=βt ,T=1000 的情况下,在 ImageNet 64x64 上训练 200k iter 时, log-likelihood = 3.99。
本文作者尝试将 T=4000 时,log-likelihood 提升到了 3.77。
将固定方差变成可学习的方差:
-
在 DDPM 中, ∑ θ ( x t , t ) = σ t 2 I \sum_{\theta}(x_t,t)=\sigma_t^2I ∑θ(xt,t)=σt2I,其中 σ t \sigma_t σt 是不可学习的,是固定成了 σ t = β t \sigma_t=\beta_t σt=βt,且和 σ t 2 = β ˜ t \sigma_t^2=\~{\beta}_t σt2=β˜t 时的采样效果没什么大的差别
-
一般来说, β t \beta_t βt 和 β ˜ t \~{\beta}_t β˜t 表示了两种相反的极端,但为什么这种选择不会影响采样结果呢。如图 1 所示,展示了两者相除的结果,可以看出 β t \beta_t βt 和 β ˜ t \~{\beta}_t β˜t 除了在 t=0 附近不太相同以外,在后面的部分相除的结果都接近于 1,且随着 T 的增大,这两者更加接近。这就说明在无限增大扩散步骤时, σ t \sigma_t σt 的选择对采样质量影响不大。也就是在使用更多的扩散步骤时,模型的平均值 μ θ ( x t , t ) \mu_{\theta}(x_t, t) μθ(xt,t) 比方差 ∑ θ ( x t , t ) \sum_{\theta}(x_t,t) ∑θ(xt,t) 更能决定这个分布。
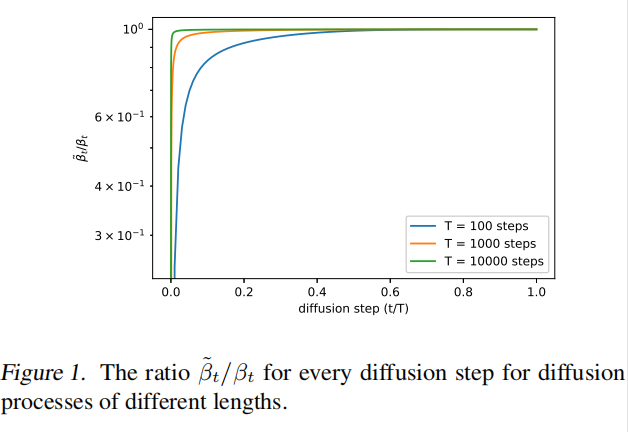
-
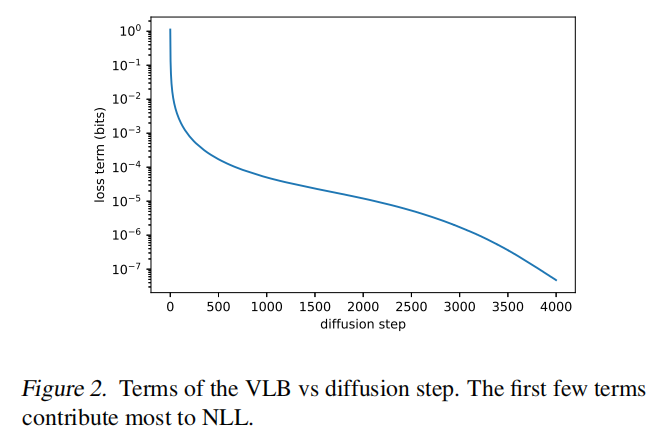
Improved DDPM 想如何改进:本文作者认为,虽然 DDPM 中证明了固定的 σ t \sigma_t σt 基本上不会影响采样的效果,但没说不会影响 log-likelihood 啊!所以,Improved DDPM 作者觉得可能会影响 log-likelihood,于是就在图 2 中展示了扩散模型的前几个 step 对变分下界的影响,而且发现了前几个 step 对变分下届的贡献最大,所以,似乎可以通过选择更好的 ∑ θ ( x t , t ) \sum_{\theta}(x_t,t) ∑θ(xt,t) 来提高 log-likelihood,所以,Improved DDPM 选择了学习 ∑ θ ( x t , t ) \sum_{\theta}(x_t,t) ∑θ(xt,t),而非固定的模式。
如何学习 ∑ θ ( x t , t ) \sum_{\theta}(x_t,t) ∑θ(xt,t):
-
如图 1 所示, ∑ θ ( x t , t ) \sum_{\theta}(x_t,t) ∑θ(xt,t) 的变化范围很小,所以很难直接使用神经网络来预测这个值
-
本文作者发现将其参数化为在 β t \beta_t βt 和 β ˜ t \~{\beta}_t β˜t 在 log domain 之间的插值,也就是说模型输出一个向量 v v v,每个维度包含一个元素,使用如下的方式将输出变成方差:
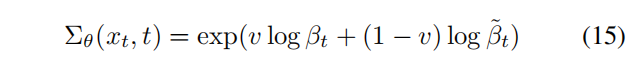
-
而且没有对 v v v 进行额外的约束,但其也不会越界。所以最终的目标函数如下,且 λ = 0.001 \lambda=0.001 λ=0.001

2.2 改进 noise schedule
在 DDPM 中使用的是线性加噪的方式,在高分辨率的图上表现的较好,但对 64x64 和 32x32 的图来说,并非最优的。
前向加噪过程是随机的,且对后面的采样过程也不很重要。加噪过程如图 3 所示。

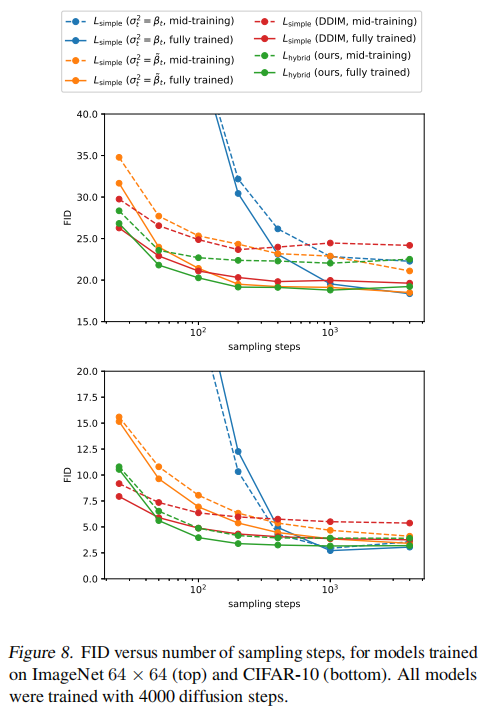
影响如图 4 所示,当跳过 20% 的反向过程时,使用线性加噪规则训练的模型(橘色)也不会变得更糟(使用 FID 衡量)。
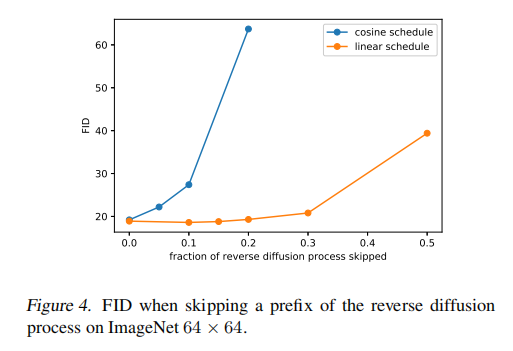
因此,本文作者提出了余弦加噪方式:

- 这里使用的偏移 s 很小,是为了在 t=0 附近让 β t \beta_t βt 更小
- 因为作者发现,在开始的时候噪声小的话,无法让网络很准确的预测 ϵ \epsilon ϵ,所以 s=0.008.
- 作者使用 c o s 2 cos^2 cos2 的原因是它是一个常见的期望形状的数学函数,选择也是任意的。
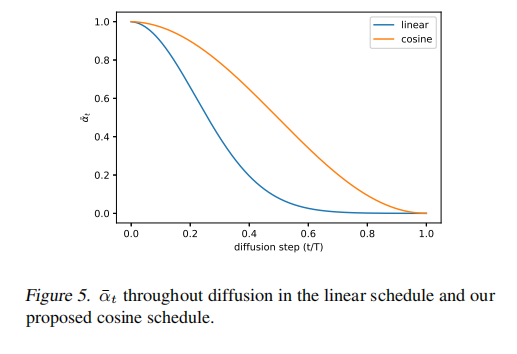
余弦加噪的特点:
- 在中间过程优一个线性的下降
- 在 t=0 和 t=T 附近,变化很小
线性加噪的特点:
- 下降到 0 的速度更快,所以破坏信息的速度更快
2.3 降低梯度噪声
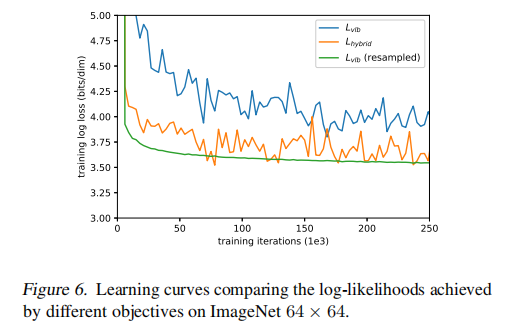
本文是为了通过直接优化 L v l b L_{vlb} Lvlb 来得到最好的 log-likelihood,而不是优化 L h y b r i d L_{hybrid} Lhybrid
然而,作者发现 L v l b L_{vlb} Lvlb 实际上很难直接优化,至少在变化多样的 ImageNet 64x64 上很难优化。
如图 6 展示了 L v l b L_{vlb} Lvlb 和 L h y b r i d L_{hybrid} Lhybrid 的学习曲线,两个曲线都很 noisy,就是不稳定,波动很大,但是橘色的 L h y b r i d L_{hybrid} Lhybrid 在同样训练步数的情况下的效果是更好一些的。
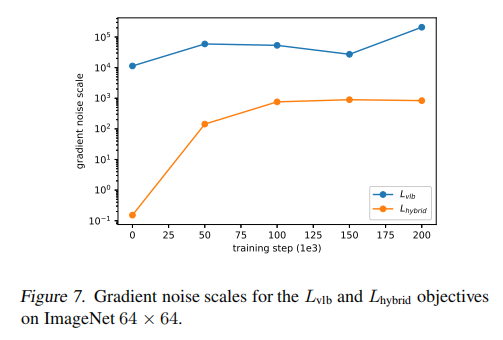
作者假设 L v l b L_{vlb} Lvlb 的梯度比 L h y b r i d L_{hybrid} Lhybrid 更 noisy,且通过衡量其梯度的 noisy scales 确定了这一点,如图 7 所示,所以,作者找到了一种降低 L v l b L_{vlb} Lvlb 方差的方法来直接优化 log-likelihood
如图 2 所示, L v l b L_{vlb} Lvlb 的不太项有不同的模值,所以假设采样 t 会在 L v l b L_{vlb} Lvlb 目标函数中带来均匀的噪声,所以作者使用了 importance sampling :
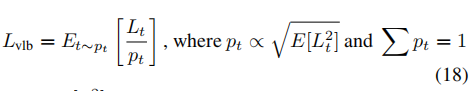
- 由于 E [ L t 2 ] E[L_t^2] E[Lt2] 是事先不知道的,也会在训练的时候改变,所以会保留前 10 次的值,且在训练的时候动态更新。
有了这个 importance sampling 方法,就能够通过优化 L v l b L_{vlb} Lvlb 来实现最佳的 log-likelihood。如图 6,而且 importance sampling 的噪声比原始均匀采样的目标函数小得多。
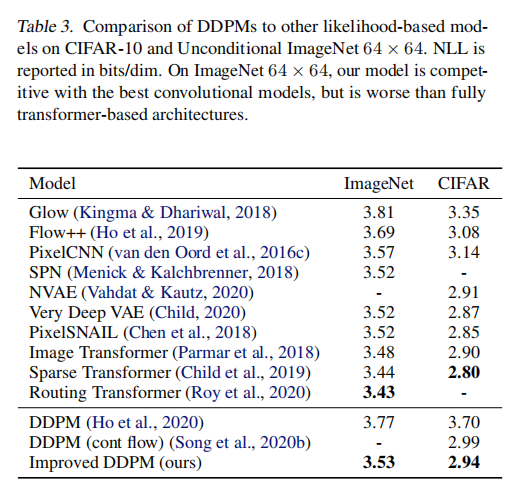
三、效果