目录
目录
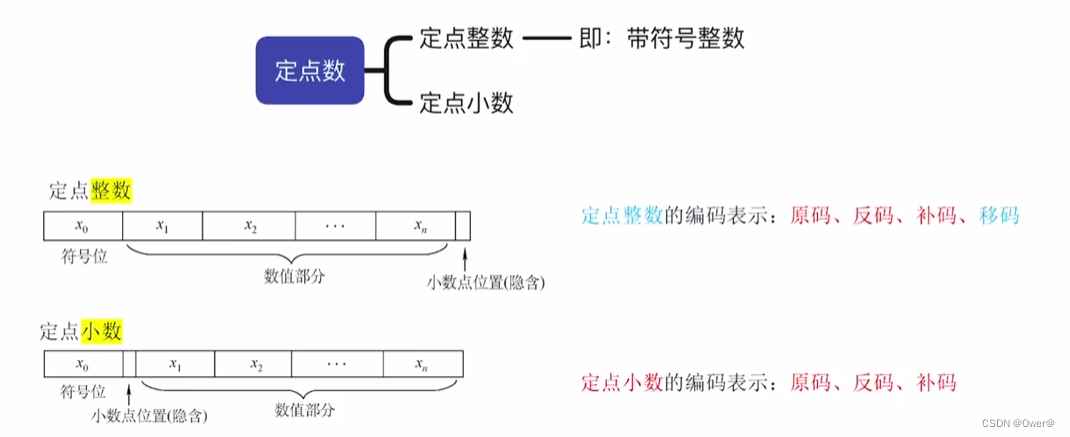
定点小数与定点整数
定点小数原反补的转换
定点小数与定点整数的取值范围
位数扩展的区别
浮点数的格式
浮点数的规格化
规格化处理举例
例1：
例2：
特例：
知识点总结：
浮点数的IEEE754标准
移码的回顾：
IEEE754标准规定
浮点型规格化的范围
定点小数与定点整数
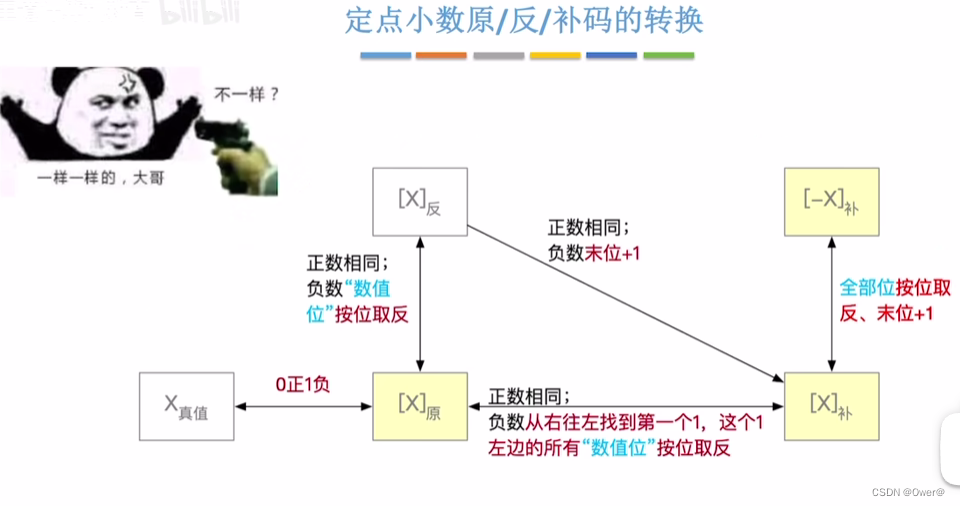
定点小数原反补的转换
同整数相同
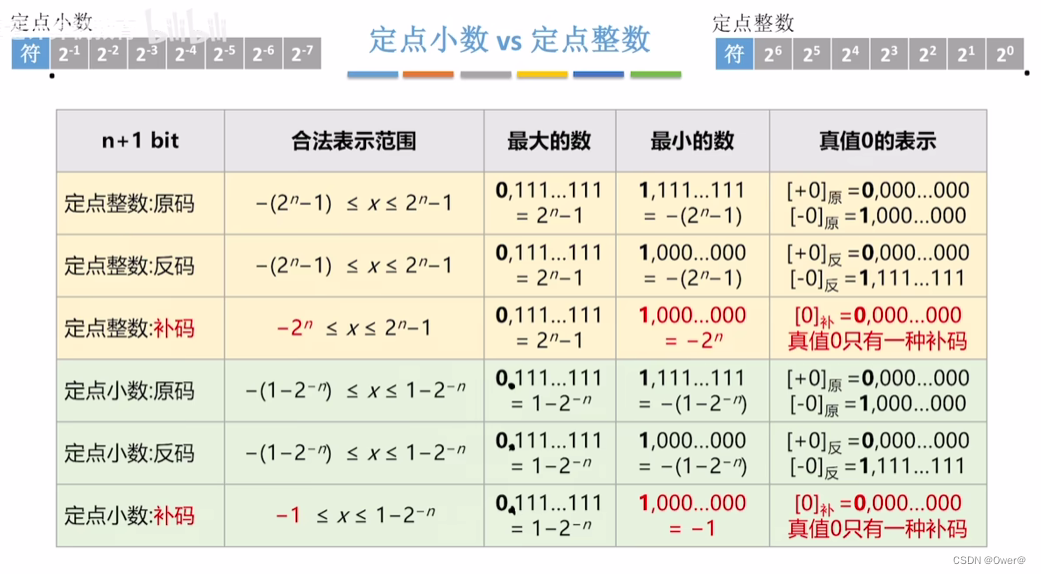
定点小数与定点整数的取值范围
↓ ↓ ↓ 注意：此时范围中的权值n是数值位的个数
位数扩展的区别
根据人为认定的小数点的位置进行位数的扩展。定点整数的默认小数点位置为低位后，扩展时在高位补0.定点小数的默认小数点位置为符号位后，扩展时在低位补0.
浮点数的格式
当二进制位数不变的情况下，通过浮点数增加数据的表示范围。注意：阶码只能为定点整数，尾数用定点小数
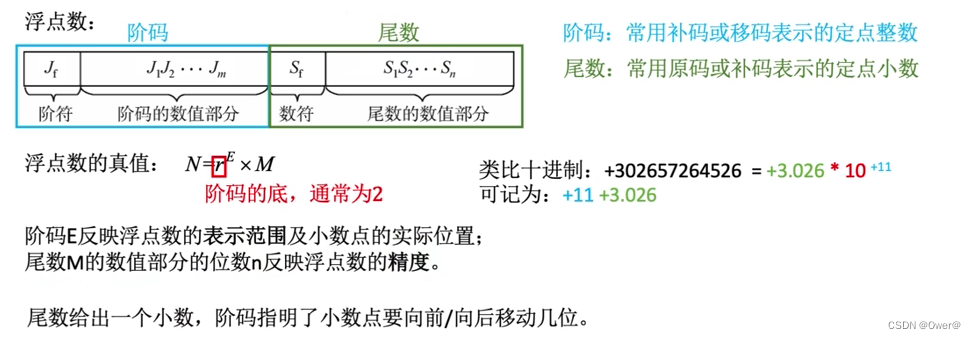
浮点数的规格化
在存储单元存储数据时，为尽可能多的存储有效的数据，提高运算的精度，充分利用尾数的有限位数，进行浮点数的规格化。
规格化的规定：当浮点数的尾数不为0时，尾数的最高位尽可能为有效位。当尾数是由原码构成时，规格化浮点数的尾数数值部分最高位为1。当尾数是由补码构成时，规格化浮点数的尾数的符号位和数值的最高位一般为10或01，符号位与数值的最高位相反。
进行规格化处理时，尾数左移即小数点右移时，阶码减一；尾数右移即小数点左移时，阶码加1。
规格化处理举例
例1：
真值N=-0.0010110 x 2^011，显然不符合规格化要求，将尾数左移两位，即小数点右移两位，同时阶码减2，规格化后的真值为 -0.10110 x 2^001.
例2：
阶码为4位，尾数为8位（包括符号位），阶码尾数都采用补码的形式。
0011 1 1101100
特例：
尾数采用补码的形式，当尾数为-0.5时，对应的补码为1.1000000。最高位与符号位相同，也满足规格化的要求。数据真值为-0.1000000 x 2^011 浮点格式为 0011 1 1000000。
知识点总结：
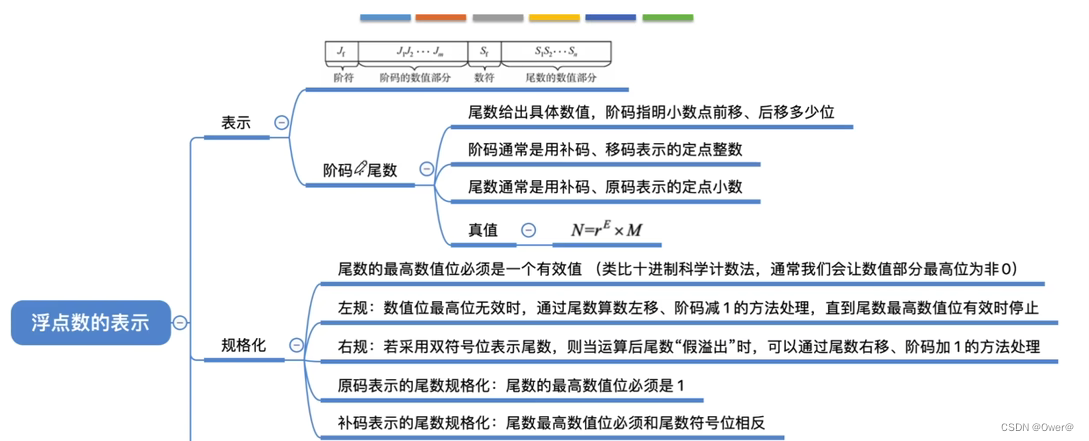
浮点数的IEEE754标准
移码的回顾：
当移码中的偏置值为2^n-1 - 1.特别注意 移码全1真值为-128，全0真值为-127。
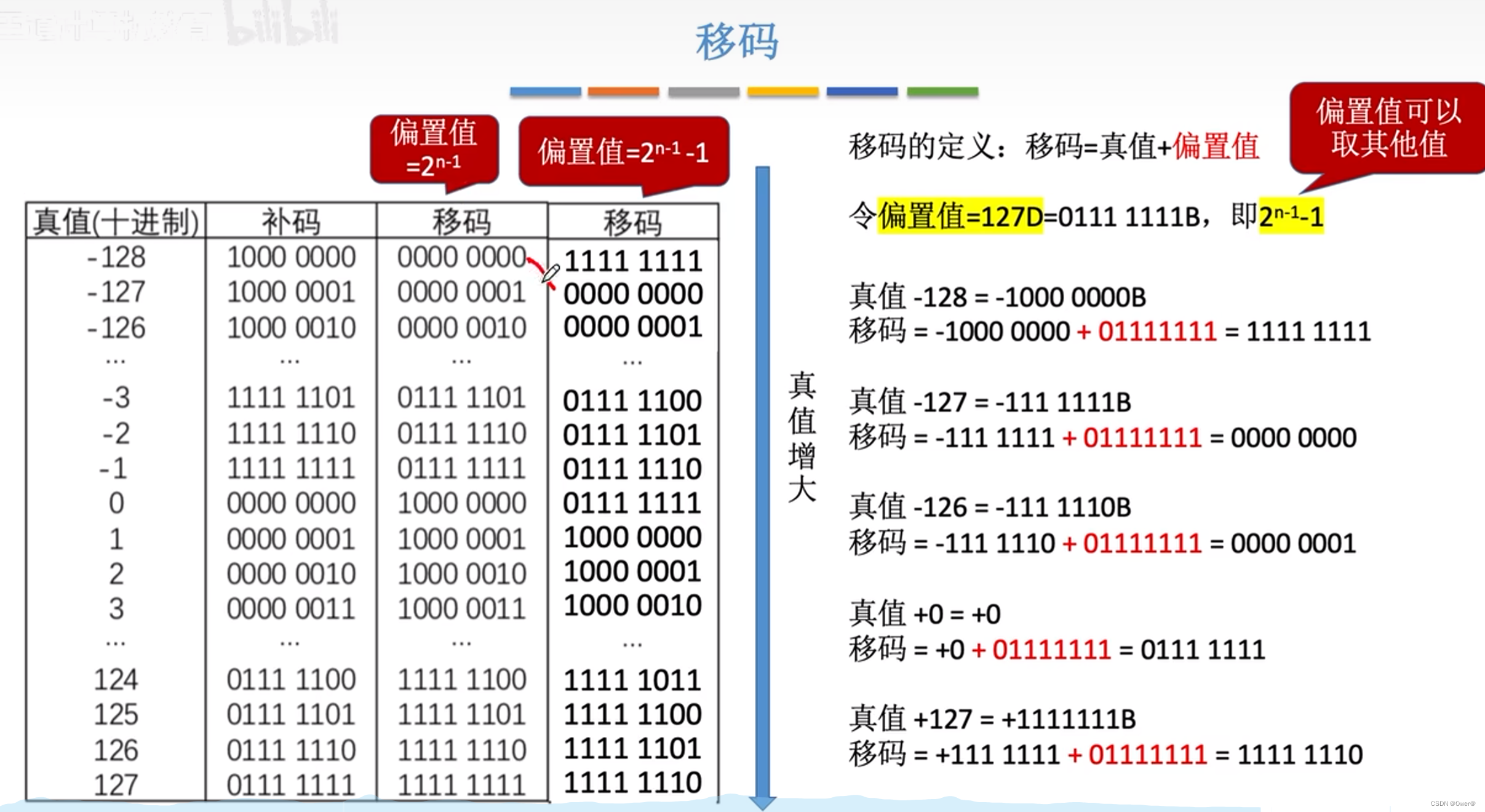
IEEE754标准规定
1、 浮点数：基数为2，尾数为原码的形式，阶码为移码的形式。其中尾数的规格化时最高位为1，该标准默认最高位为1，隐藏表示最高位1，使尾数的实际位数比存储多1，尾数的定义形式为 1.M。
IEEE754的真值表示：（-1)^S X (1.M) X 2^(E-K) , （-1)^S 判断正负号，1.M为尾数，k为偏置值。
2、 规定三种浮点的格式，单精度（短浮点数）、双精度（长浮点数）、扩展精度（临时浮点数）。组成的格式为，符号位+阶码+尾数。其中阶码的偏置值是以 2^n-1 - 1计算的，阶码的真值的范围为 -126~127，（其中的-127、-128是阶码全0、全1用作特殊用途）。公式阶码的真值=移码-偏置值。
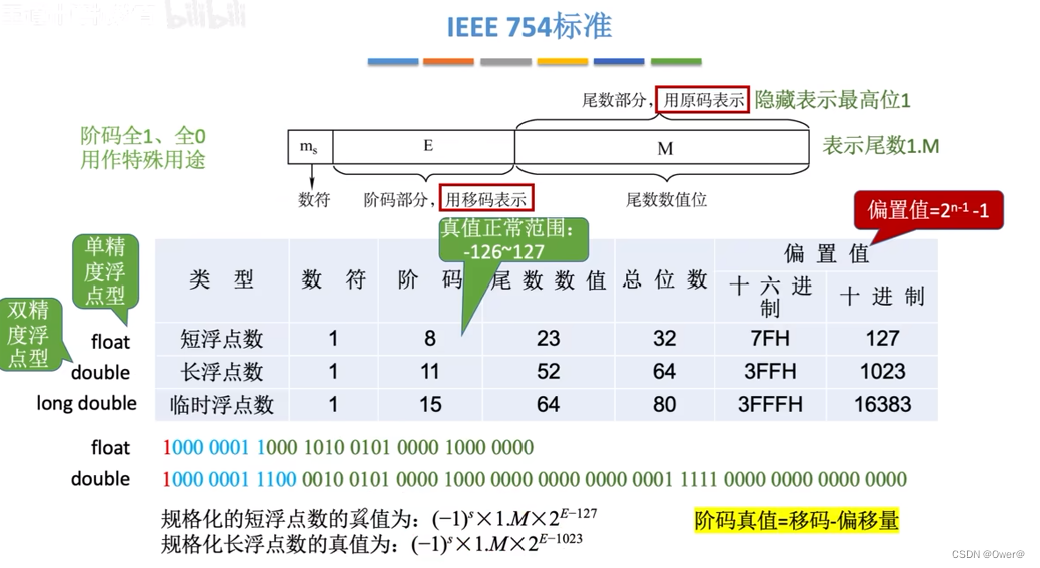
浮点型规格化的范围
↓ 待回顾，暂时没理解
图片和配套 视频来源 王道计算机组成原理 :https://www.bilibili.com/video/BV1ps4y1d73V?p=1&vd_source=52fd23976808a6e9645ad9b31999a484
https://www.bilibili.com/video/BV1ps4y1d73V?p=1&vd_source=52fd23976808a6e9645ad9b31999a484
