P ( x t P(x_t P(xt| x t − 1 ) x_{t-1}) xt−1) | P ( y t P(y_t P(yt| x t ) x_t) xt) | P ( x 1 ) P(x_1) P(x1) | |
|---|---|---|---|
| Discrete State DM | A X t − 1 , X t A_{X_{t-1},X_t} AXt−1,Xt | Any | π \pi π |
| Linear Gassian Kalman DM | N ( A X t − 1 + B , Q ) N(AX_{t-1}+B,Q) N(AXt−1+B,Q) | N ( H X t + C , R ) N(HX_t+C,R) N(HXt+C,R) | N ( μ 0 , ϵ 0 ) N(\mu_0,\epsilon_0) N(μ0,ϵ0) |
| No-Linear NoGaussian DM | f ( x t − 1 ) f(x_{t-1}) f(xt−1) | g ( y t ) g(y_t) g(yt) | f ( x 1 ) f(x_1) f(x1) |
{ P ( y 1 , . . . , y t ) − − e v a l u a t i o n a r g m e n t θ log P ( y 1 , . . . , y t ∣ θ ) − − p a r a m e t e r l e a r n i n g P ( x 1 , . . . , x t ∣ y 1 , . . . , y t ) − s t a t e d e c o d i n g P ( x t ∣ y 1 , . . , y t ) − f i l t e r i n g \left\{ \begin{aligned} P(y_1,...,y_t)--evaluation\\ argment \theta \log{P(y1,...,y_t|\theta)}--parameter learning \\ P(x_1,...,x_t|y_1,...,y_t)-state decoding \\ P(x_t | y_1,..,y_t)-filtering \end{aligned} \right. ⎩ ⎨ ⎧P(y1,...,yt)−−evaluationargmentθlogP(y1,...,yt∣θ)−−parameterlearningP(x1,...,xt∣y1,...,yt)−statedecodingP(xt∣y1,..,yt)−filtering
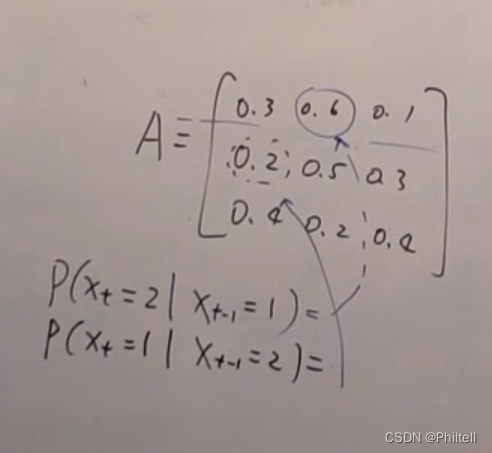
线性高斯噪声的动态模型
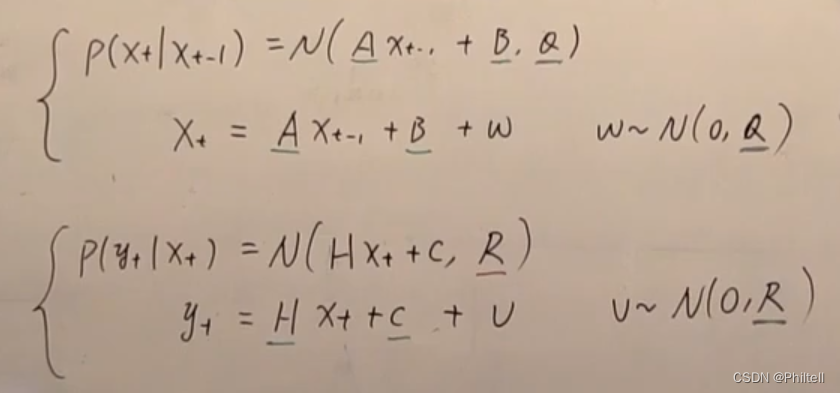
P ( x t ∣ y 1 , . . . , y t ) P(x_t|y_1,...,y_t) P(xt∣y1,...,yt)
假设转移概率是 P ( x t ∣ X t − 1 ) = N ( A X t − 1 + B , Q ) P(x_t|X_{t-1})= N(AX_{t-1}+B,Q) P(xt∣Xt−1)=N(AXt−1+B,Q)
X t = A X t − 1 + B + ω X_t = AX_{t-1}+B+\omega Xt=AXt−1+B+ω , ω ∼ N ( 0 , Q ) \omega \sim N(0,Q) ω∼N(0,Q)
measurement probility
P ( y t ∣ x t ) = N ( H X t + C , R ) P(y_t|x_t) = N(HX_t+C,R) P(yt∣xt)=N(HXt+C,R)
y t = H X t + C + v y_t = HX_t+C+v yt=HXt+C+v
v ∼ N ( 0 , R ) v \sim N(0,R) v∼N(0,R)
以下都是参数。
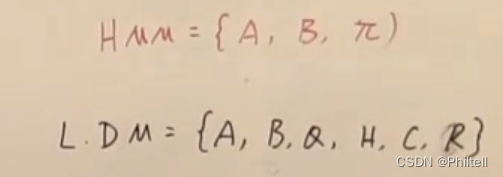
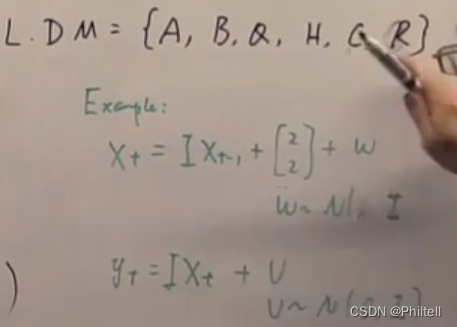


filter公式推导


HMM模型,当隐变量确定的时候,观测就变成独立的了。

- 卡尔曼滤波,当t = 1的时候,我们就知道 P ( x 1 ∣ y 1 ) ∼ N ( u ^ 1 , σ ^ 1 ) P(x_1|y_1) \sim N(\hat u_1,\hat \sigma_1) P(x1∣y1)∼N(u^1,σ^1)
- t = 2的时候, P ( x 2 ∣ y 2 ) ∼ N ( u ‾ 2 , σ ‾ 2 ) P(x_2|y_2) \sim N(\overline u_2,\overline \sigma_2) P(x2∣y2)∼N(u2,σ2)

个人理解
- 卡尔曼滤波可以理解为滤波器的一种,用数学表达就是用观测量 y 1 , y 2 , y 3 . . . , y t y_1,y_2,y_3...,y_t y1,y2,y3...,yt来获得t时刻的估计量 x t x_t xt,数学公式为
P ( x t ∣ y 1 , . . . , y t ) P(x_t|y_1,...,y_t) P(xt∣y1,...,yt)正比与 P ( x t , y 1 , . . . , y t ) P(x_t,y_1,...,y_t) P(xt,y1,...,yt)可以理解为前置条件 y 1 , . . . , y t y_1,...,y_t y1,...,yt发生的条件下有发生 x t x_t xt的概率与两类事件同时发生的概率是成正比的。可以简单理解为 P ( A ∣ B ) P(A|B) P(A∣B)与 P ( A , B ) P(A,B) P(A,B)成正比。 - 那么得出 P ( x t ∣ y 1 , . . . , y t ) ∝ P ( x t , y 1 , . . . , y t ) ∝ P ( y t ∣ x t , y 1 , . . . , y t − 1 ) ∗ P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_t) \propto P(x_t,y_1,...,y_t) \propto P(y_t|x_t,y_1,...,y_{t-1}) * P(x_t|y_1,...,y_{t-1}) P(xt∣y1,...,yt)∝P(xt,y1,...,yt)∝P(yt∣xt,y1,...,yt−1)∗P(xt∣y1,...,yt−1)
- 有HMM可以得知, P ( y t ) P(y_t) P(yt)发生的概率是只跟 x t x_t xt相关,因此 P ( y t ∣ x t , y 1 , . . . , y t − 1 ) = P ( y t ∣ x t ) P(y_t|x_t,y_1,...,y_t-1) = P(y_t|x_t) P(yt∣xt,y1,...,yt−1)=P(yt∣xt),而 x t x_t xt的估计量,是通过上一次观测获得, x t x_t xt与 y 1 , . . . , y t − 1 y_1,...,y_{t-1} y1,...,yt−1相关。
- 那么得出预测为 P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_{t-1}) P(xt∣y1,...,yt−1),前t-1时刻的观测值估计下一刻t的状态。
- 将 x t x_t xt看为常量,将 x t − 1 x_{t-1} xt−1看为变量,那么就得到了预测公式的推导公式为 P ( x t ∣ y 1 , . . . , y t − 1 ) = ∫ d ( x t − 1 ) P ( x t , x t − 1 ∣ y 1 , . . . , y t ) d x t − 1 ∝ ∫ x t − 1 P ( x t ∣ x t − 1 ) P ( x t − 1 ∣ y 1 , . . . , y t − 1 ) d ( x t − 1 ) P(x_t|y_1,...,y_{t-1})=\int_{d(x_{t-1})}{P(x_t,x_{t-1}|y_1,...,y_t)dx_{t-1}} \propto \int_{x_{t-1}}P(x_t|x_{t-1})P(x_{t-1}|y_1,...,y_{t-1})d(x_{t-1}) P(xt∣y1,...,yt−1)=∫d(xt−1)P(xt,xt−1∣y1,...,yt)dxt−1∝∫xt−1P(xt∣xt−1)P(xt−1∣y1,...,yt−1)d(xt−1)

总结
- 预测:不知道当前时刻的观测,用上一时刻观测与预测当前时刻的状态
P ( x t ∣ y 1 , . . . , y t − 1 ) = ∫ P ( x t ∣ x t − 1 ) P ( x t − 1 ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_{t-1})= \int P(x_t|x_{t-1})P(x_{t-1}|y_1,...,y_{t-1}) P(xt∣y1,...,yt−1)=∫P(xt∣xt−1)P(xt−1∣y1,...,yt−1) - 更新:已经知道当前时刻的观测,用当前的观测更新当前可是的状态
P ( x t ∣ y 1 , . . . , y t ) = P ( y t ∣ x t ) P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_t)=P(y_t|x_t)P(x_t|y_1,...,y_{t-1}) P(xt∣y1,...,yt)=P(yt∣xt)P(xt∣y1,...,yt−1)



结论
- x t ∣ y 1 , . . . , y t − 1 = A E [ x t − 1 ] + A Δ X t − 1 + ω x_t|y_1,...,y_{t-1}=AE[x_{t-1}]+A\Delta X_{t-1}+\omega xt∣y1,...,yt−1=AE[xt−1]+AΔXt−1+ω = E [ x t ] + Δ x t =E[x_t]+\Delta x_t =E[xt]+Δxt
- y t ∣ y 1 , . . . y t − 1 = H A E [ X t − 1 ] + H A Δ x t − 1 + H ω + v = E [ y t ] + Δ y t y_t|y_1,...y_{t-1} = HAE[X_{t-1}]+HA \Delta x_{t-1}+H\omega + v = E[y_t] + \Delta y_t yt∣y1,...yt−1=HAE[Xt−1]+HAΔxt−1+Hω+v=E[yt]+Δyt
- P ( x t ∣ y 1 , . . . , y t ) = N ( A E [ x t − 1 ] , E [ ( Δ x ) ( Δ x ) T ] ) P(x_t|y_1,...,y_t) = N(AE[x_{t-1}],E[(\Delta x)(\Delta x)^T]) P(xt∣y1,...,yt)=N(AE[xt−1],E[(Δx)(Δx)T])
- P ( y t ∣ y 1 , . . . , y t − 1 ) = N ( H A E [ X t − 1 ] , E [ ( Δ y ) ( Δ y ) T ] ) P(y_t|y1,...,y_{t-1}) = N(HAE[X_{t-1}],E[(\Delta y)(\Delta y)^T]) P(yt∣y1,...,yt−1)=N(HAE[Xt−1],E[(Δy)(Δy)T])
以上为边缘分布
P ( x t , y t ∣ y 1 , . . . , y t − 1 ) P(x_t,y_t|y_1,...,y_{t-1}) P(xt,yt∣y1,...,yt−1)