目录

算法简述

基本

典型算法列举

串和串的匹配

排序

深度/广度优先搜索

动态规划

分治

贪心

回溯

分支限界

---

算法简述

基本

咳咳嗯…算法嘛，咱也不是 CS 科班学生，咱就说，算法是对已经建模后的问题的解决的具体途径和方法，是学习 对于编程来讲的 一些 已经成熟/成型的 完成问题的计算的 套路和思想。

典型算法列举

串和串的匹配

基本

串（string）是由零个或多个字符组成的有限序列，又名叫字符串。一个串（流口水）中任意个连续的字符组成的子序列为该串的子串。串的编码方式即字符编码如 ASCII编码、Unicode编码等。

串中的元素都是字符，串的操作主要与 字符串的操作 而非 单个元素 有关，其多为 查找子串位置、得到指定位置子串、替换子串等操作，如下：

显而易见，标准库如 string.h 给出了串的基本操作 API，关于 C 标准库的详细使用可参考 “C & MCU编写规范和其他” 一文的 “7 C 标准库的使用” 一节。

串的匹配算法（也可叫串的模式匹配）

串匹配，比如：要从主串 S = “BBC ABCDAB ABCDADCDABDE” 中 找到 与 模式串 P = “ABCDABD” 相同的 子串 的位置。

串的模式匹配算法-BF算法（或叫暴力算法）

主串 S 从 i = 0 位置开始与 模式串 P 从 j = 0 位置开始一个字符一个字符的匹配是否一样，如果相同则 i 和 j 均加一然后再判断是否匹配，若不同则 i 回到 这次匹配开始的位置同时 j 回到首位，继续挨个匹配。一图说明：

引自：21 串模式匹配算法（BF算法） - 知乎 (zhihu.com)

串的快速模式匹配算法-KMP算法

主要思想就是相比于 BF 算法，为了加速匹配，找一些规律，当匹配失效的时候 j 不用每次回到 P 的 开头位置，而是根据（注意，不了解的推荐先看下面给出的教程文章，这里是明白后的总结） 模式串的 各个字串的 各个前缀、后缀子串的 最大公共元素长度 来构造 next 数组，j 每次移动的位数根据 next 来调整。

• 从头到尾彻底理解KMP - Chris_z - 博客园 (cnblogs.com)。Coding-Zuo (cnblogs.com)。该文讲的很清楚。
• 「天勤公开课」KMP算法易懂版_ 哔哩哔哩 _bilibili。

排序

• 十大经典排序算法（动图演示） - 一像素 - 博客园 (cnblogs.com)。
• 算法大总结之—-10大经典排序算法(从小到大排列)_ Frank的博客-CSDN博客 _从小到大排序算法。

深度/广度优先搜索

图的遍历 通常采用 深优先搜索（DFS） 与 广度优先搜索（BFS） 方式进行。“如果把树看做一种特殊的图的话，DFS 就是前序遍历”。

• 搜索思想——DFS & BFS（基础基础篇） - 知乎 (zhihu.com)。
• 搜索思想——DFS & BFS（基础篇） - 知乎 (zhihu.com)。
• 图的深度优先搜索（DFS）与广度优先搜索（BFS）_青萍之末的博客-CSDN博客。
• 深度优先遍历与连通分量 | 菜鸟教程 (runoob.com)，广度优先遍历与最短路径 | 菜鸟教程 (runoob.com)。

动态规划

• 什么是动态规划（Dynamic Programming）？动态规划的意义是什么？ - 知乎 (zhihu.com)。
• DP-动态规划问题心得 - 知乎 (zhihu.com)。
• 一只脚迈进DP的海洋 - 知乎 (zhihu.com)。
• 五大常用算法——动态规划算法详解及经典例题_ 别再想更好的办法的博客-CSDN博客 _动态规划算法经典例题。

有的人理解为用“动态规划”的思想（写出优化目标和状态转移方程（或者叫递归关系式））去理解和建模问题使得找出问题的优化解可以不用遍历所有可能解（剪枝，或去除不可能为最优解的计算从而节省时间，或者去除重叠的子问题）；常用一种实现方法为用缓存存储数据来减少重复计算（把穷举的计算过程展开为一棵树，然后找出其中重复计算的部分，用缓存来保留一份之前要重复计算的结果，来减少重复计算），还有其它许多技巧和方法。

分治

引自：五大常用算法——分治算法详解及经典例题_ 别再想更好的办法的博客-CSDN博客 _分治算法经典例题。

分治法的设计思想是：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

分治策略是：对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。

如果原问题可分割成k个子问题，1<k≤n，且这些子问题都可解并可利用这些子问题的解求出原问题的解，那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

可使用分治法求解的一些经典问题：

• （1）二分搜索
• （2）大整数乘法
• （3）Strassen矩阵乘法
• （4）棋盘覆盖
• （5）合并排序
• （6）快速排序
• （7）线性时间选择
• （8）最接近点对问题
• （9）循环赛日程表
• （10）汉诺塔

分治算法的一个核心在于子问题的规模大小是否接近，如果接近则算法效率较高。

分治算法和动态规划都是解决子问题，然后对解进行合并；但是分治算法是寻找远小于原问题的子问题（因为对于计算机来说计算小数据的问题还是很快的），同时分治算法的效率并不一定好，而动态规划的效率取决于子问题的个数的多少，子问题的个数远小于子问题的总数的情况下（也就是重复子问题多），算法才会很高效。

• 五大常用算法——分治算法详解及经典例题_ 别再想更好的办法的博客-CSDN博客 _分治算法经典例题。

贪心

引自：五大常用算法——贪心算法详解及经典例子_ 别再想更好的办法的博客-CSDN博客 _贪心算法。

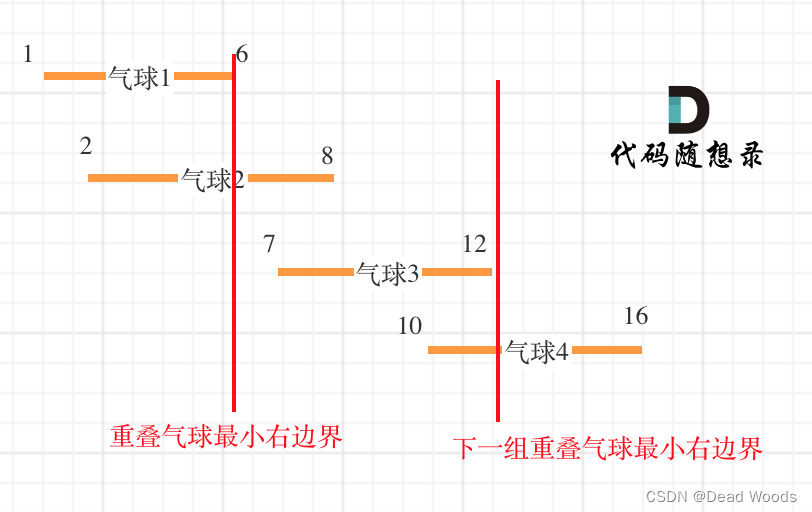
贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。

基本思路

1. 建立数学模型来描述问题。

2. 把求解的问题分成若干个子问题。

3. 对每一子问题求解，得到子问题的局部最优解。

4. 把子问题的解局部最优解合成原来解问题的一个解。

实现该算法的过程

1. 从问题的某一初始解出发；

2. while 能朝给定总目标前进一步 do；

3. 求出可行解的一个解元素；

4. 由所有解元素组合成问题的一个可行解。

该算法存在问题

1. 不能保证求得的最后解是最佳的；
2. 不能用来求最大或最小解问题；
3. 只能求满足某些约束条件的可行解的范围。

引自：什么是动态规划（Dynamic Programming）？动态规划的意义是什么？ - 知乎 (zhihu.com) 来说明贪心算法的缺陷：　

先来看看生活中经常遇到的事吧——假设您是个土豪，身上带了足够的1、5、10、20、50、100元面值的钞票。现在您的目标是凑出某个金额w，需要用到尽量少的钞票。

依据生活经验，我们显然可以采取这样的策略：能用100的就尽量用100的，否则尽量用50的……依次类推。在这种策略下，666=6×100+1×50+1×10+1×5+1×1，共使用了10张钞票。

这种策略称为“贪心”：假设我们面对的局面是“需要凑出w”，贪心策略会尽快让“还需要凑出的部分”变得更小。能让w少100就尽量让它少100，这样我们接下来面对的局面就是凑出w-100。长期的生活经验表明，贪心策略是正确的。

但是，如果我们换一组钞票的面值，贪心策略就也许不成立了。如果一个奇葩国家的钞票面额分别是1、5、11，那么我们在凑出15的时候，贪心策略会出错：

15=1×11+4×1 （贪心策略使用了5张钞票）

15=3×5 （正确的策略，只用3张钞票）

为什么会这样呢？贪心策略错在了哪里？

鼠目寸光。

刚刚已经说过，贪心策略的纲领是：“尽量使接下来面对的w更小”。这样，贪心策略在w=15的局面时，会优先使用11来把w降到4；但是在这个问题中，凑出4的代价是很高的，必须使用4×1。如果使用了5，w会降为10，虽然没有4那么小，但是凑出10只需要两张5元。

在这里我们发现，贪心是一种只考虑眼前情况的策略。

• 五大常用算法——贪心算法详解及经典例子_ 别再想更好的办法的博客-CSDN博客 _贪心算法。

回溯

引自：leetcode回溯算法（backtracking） 总结_wonner_的博客-CSDN博客 _leetcode 回溯。

回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。

• 回溯算法详解及Leetcode经典例题解答_ 芒果就是没有盲的博客-CSDN博客 _回溯算法leetcode。
• leetcode回溯算法（backtracking）总结_ wonner_的博客-CSDN博客 _leetcode 回溯。
• 五大常用算法——回溯算法详解及经典例题_ 别再想更好的办法的博客-CSDN博客 _回溯算法经典例题。

分支限界

引自：五大常用算法——分支限界算法详解及经典例题_ 别再想更好的办法的博客-CSDN博客 _分支定界法例题详解。

对比回溯法

• 回溯法的求解目标是找出解空间中满足约束条件的所有解，想必之下，分支限界法的求解目标则是找出满足约束条件的一个解，或是满足约束条件的解中找出使某一目标函数值达到极大或极小的解，即在某种意义下的最优解。
• 另外还有一个非常大的不同点就是，回溯法以深度优先的方式搜索解空间，而分支界限法则以广度优先的方式或以最小耗费优先的方式搜索解空间。

• 五大常用算法——分支限界算法详解及经典例题_ 别再想更好的办法的博客-CSDN博客 _分支定界法例题详解。