RBTree（红黑树）模拟实现（插入）

红黑树的性质

红黑树的模拟插入

叔叔存在且为红色

叔叔不存在

旋转情况

叔叔存在且为黑色

总结

插入实现

节点

插入逻辑

左单旋

右单旋

红黑树是一颗平衡搜索二叉树，但是红黑树并不像 AVL 树一样是高度平衡二叉树，任意一颗红黑树，它的子树不会超出它任意一个子树高度的二倍。

红黑树的性质

每个节点不是红色就是黑色
根节点是黑色的
每个叶子节点（nil 节点/空节点）都是黑色的
如果一个叶子节点是红色的，那么它的孩子节点都必须是黑色的
任意一条路径上包含的黑色节点的数量都是相等的

其中，红黑树的平衡，就是由上面五条决定的。但是这里看到上面的五条并没有提到高度等字眼，红黑树也并不靠高度来维持平衡。

所以通过上面的条件，红黑树的高度虽然比 AVL 树的高度要高，但是红黑树的旋转次数是要比 AVL 树的少的，对于计算机而言，虽然高度可能比 AVL 树高，但是就搜索树的搜索时间复杂度为 O(log n) 来说，即使是红黑树的高度要相差二倍，那么时间复杂度最差也就是 O(log 2n) ，而对于计算机来说，这点时间并不算什么。

红黑树的模拟插入

红黑树的插入也是有几种情况，这几种情况分别需要不同的对待，所以下面我们看一下。

但是在插入之前，我们先想个问题，我们在插入的时候是插入红色节点呢？还是黑色节点？

如果我们插入黑色节点，那么单条路径上的黑色节点的个数就变化了，所以我们还需要去修改其他路径的黑色节点，所以插入黑色节点的话，需要修改的节点数比较多
插入红色节点，插入红色节点的话，我们的红黑树可能就不满足了，因为如果插入节点的父亲节点是红色的，那么就不满足红色节点的孩子节点必须是黑色的，所以这时候我们就需要对它的父亲节点进行修改颜色，或者是它的叔叔，并不会像插入黑色节点那样，需要对其他的路径都做修改
所以，如果我们插入黑色节点的话，需要调整的工作量就比较大，但是如果我们插入红色节点的话，是有可能是不需要调整的，因为可能插入的节点的父亲节点就是黑色的，就算插入的父亲节点是红色的，那么也只需要修改它的父亲节点，或者是叔叔节点

叔叔存在且为红色

这里有一颗红黑树：

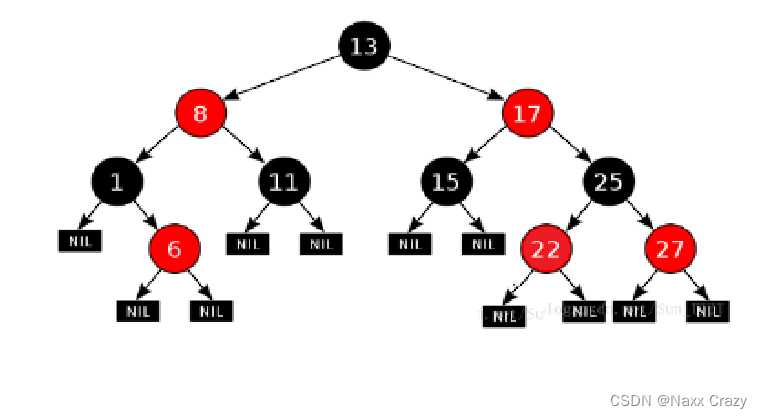
假设我们现在要插入的节点是 21：

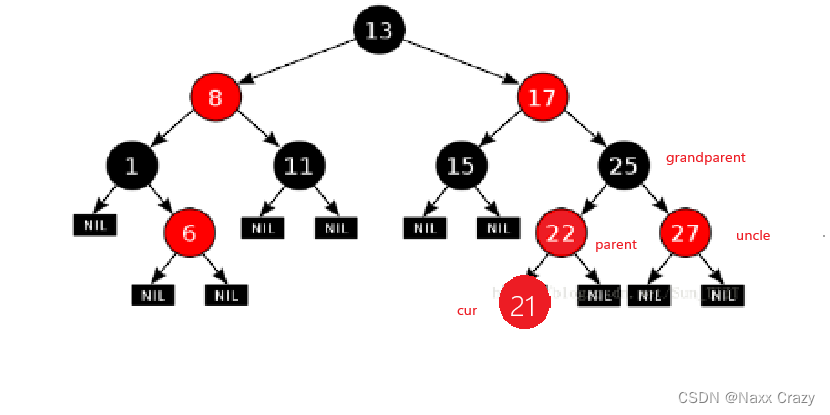
这时候，我们看到 cur 位置已经插入了节点 21，但是插入之后，该红黑树违反了，“红色节点的孩子节点必须是黑色的” 这一条规定，所以为例维持红黑树，我们需要对其进行变色，或者是旋转等操作来使其依旧是红黑树。

既然上面违反了 “红色几点的孩子节点必须是黑色的”，那么我们在看一下，cur 有没有叔叔节点，如果有的话，那么我们在看一下叔叔节点的颜色是不是红色的，如果都满足的话，那么下面我们就把父亲节点和叔叔节点都变为黑色的，然后把祖父节点变为红色，这样的话，这两条路径的黑色节点数量就不变了：

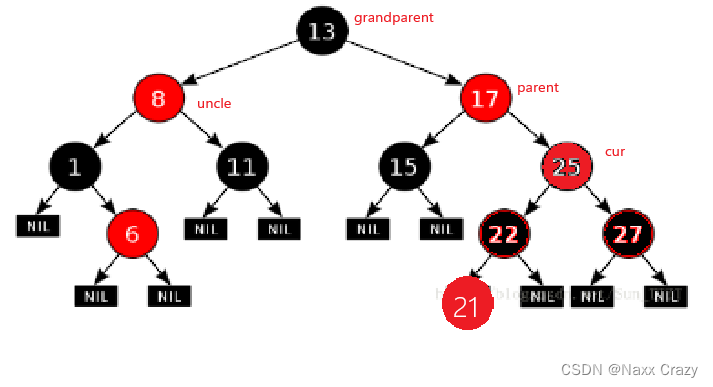
但是这里变色结束后，我们看到祖父节点是红色的，祖父节点的父亲节点也是红色的，所以我们可以继续刚才的步骤，知道祖父节点的颜色变为黑色，或者是祖父节点没有父亲节点，或者是其他情况的时候就结束，所以这时候，我们将祖父节点赋值给 cur 节点，然后继续啊上面的循环：

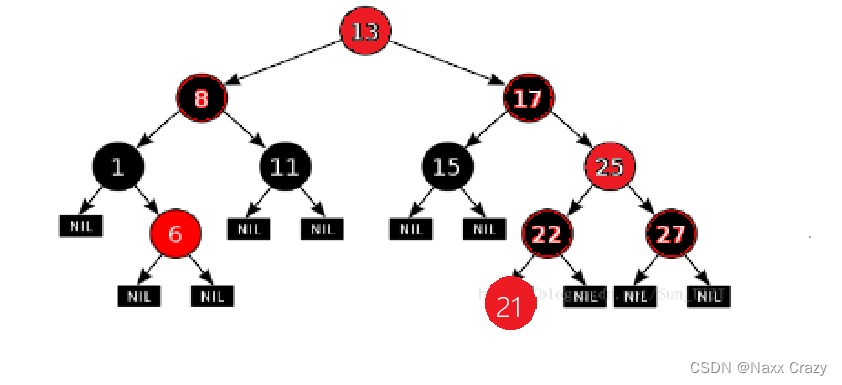
这时候，我们的祖父节点没有父亲节点，也就表示祖父节点就是根了，那么也就可以跳出循环，不过跳出循环后，我们的根节点不满足“根节点是黑色的”，这一条规定，所以出了循环之后，我们可以把根节点置为黑色：

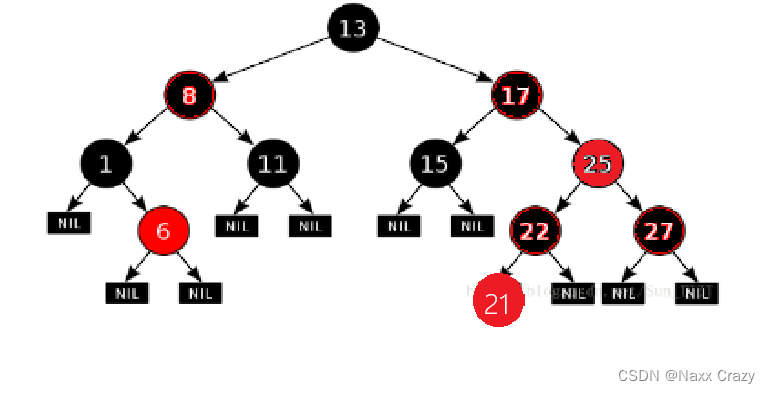
在这样变色之后，该红黑树还是红黑树。

上面就是叔叔存在且为红色的情况。

叔叔不存在

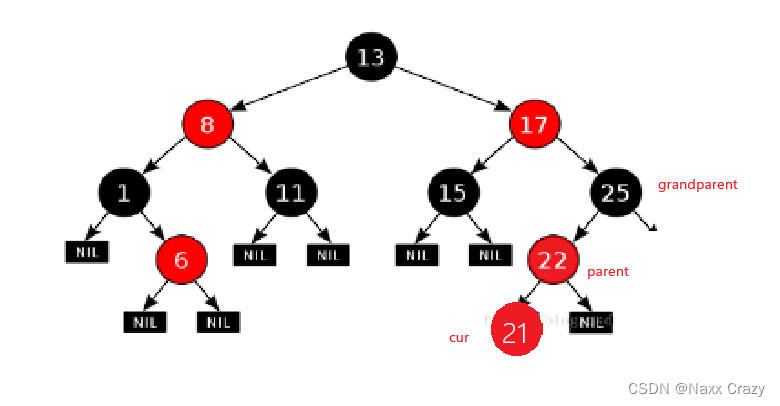
如果是这种情况的话，那么就是叔叔不存在的情况，我们已经插入了 cur 节点，而这时候就是叔叔不存在的情况，那么这时候就不能靠改变父亲的颜色来维持红黑树了，因为这里只把父亲的颜色改变后和把祖父的颜色改变后，那么最右边的路径上黑色节点的数量就变少了，与其他路径的黑色节点的数量不同，所以不能光改变父亲和祖父的颜色，这时候就需要旋转加变色，那么怎么样旋转？这里我们可以对 grandparent 节点进行右单旋，然后将 parent 节点变为黑色，祖父节点变为红色：

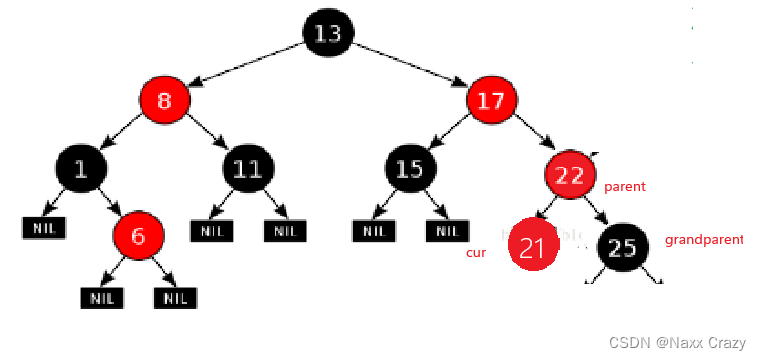
下一步就是将祖父节点变为红色，父亲节点变为黑色：

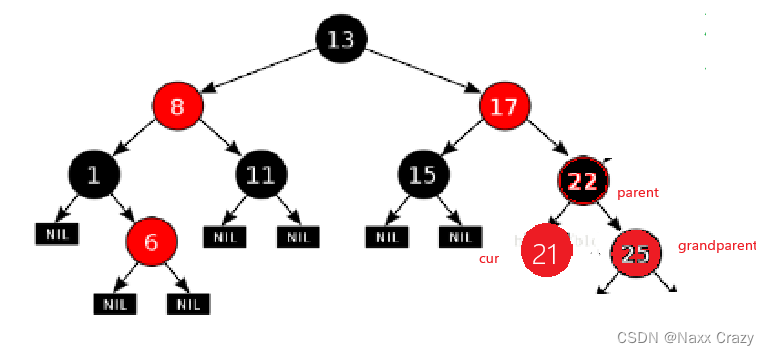
经过这样的旋转和变色之后，该树还是红黑树，不过刚才使用的是右单旋，那么怎么样判断是左单旋，还是右单旋，亦或者是右左双旋，或者是左右双旋？

旋转情况

在红黑树的旋转的判断条件并不是高度，而是看 cur parent 以及 grandparent 三个节点的位置。

1. 如果 parent 是 grandparent 的 left ，并且 cur 也是 parent 的 left ，那么就使用的是右单旋

2. 如果 parent 是 grandparent 的 right，并且 cur 也是 parent 的 right，那么就使用的是左单旋

3. 如果 parent 是 grandparent 的 right，并且 cur 也是 parent 的 left ，那么就使用的是右左双旋

4. 如果 parent 是 grandparent 的 left ，并且 cur 也是 parent 的 right，那么就使用的是左右双旋

所以下面我们看一下叔叔不存在，双旋的情况：

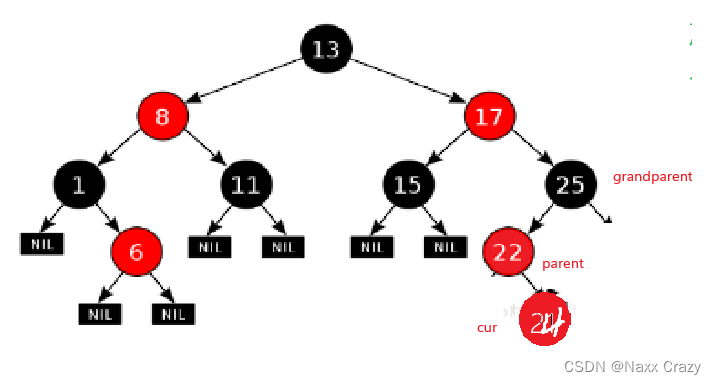
这时候，我们插入的节点是 24 这个节点，然后我们发现叔叔不存在，所以我们需要使用旋转加变色的方案，我们发现 parent 是 grandparent 的左，而 cur 是 parent 的右，所以我们需要使用左右双旋：

先对 parent 进行左单旋

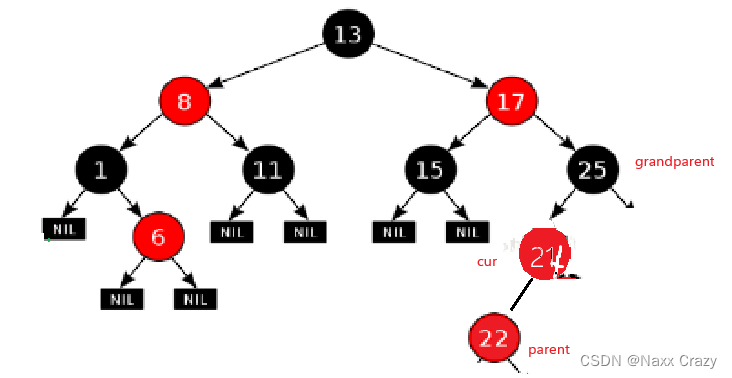
在对 grandparent 进行右单旋

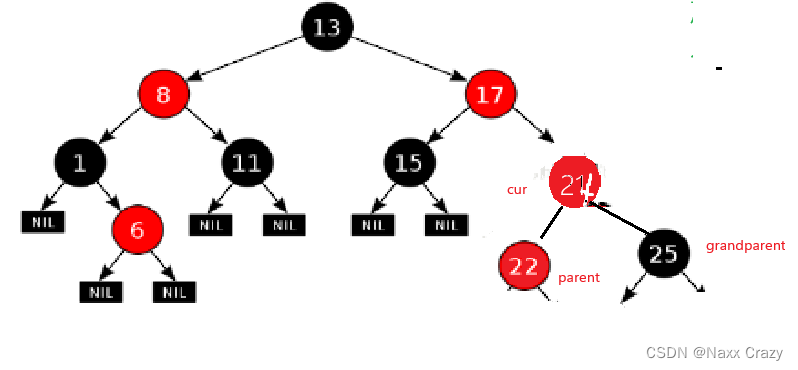
旋转结束后，我们发现颜色不正确，所以我们在这种情况下，需要将grandparent 变为红色，然后将 cur 变为黑色。

叔叔存在且为黑色

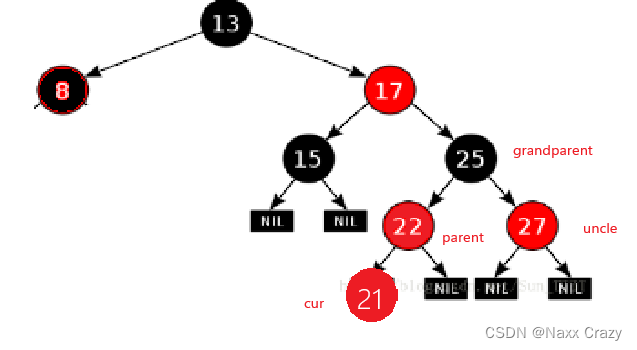
上面就是叔叔存在且为黑色，我们到 cur 位置插入，但是这里我们先进行叔叔存在且为红色，所以我们向上跟新：

到这时候，就变成叔叔存在且为黑色了，所以这时候我们也不能单靠变色来解决问题，我们需要旋转加变色。

这时候的旋转也是按照上面的规则来的，我们看到parent 是 grandparent 的右边，cur 是 parent 的右边所以这时候我们使用的是左单旋：

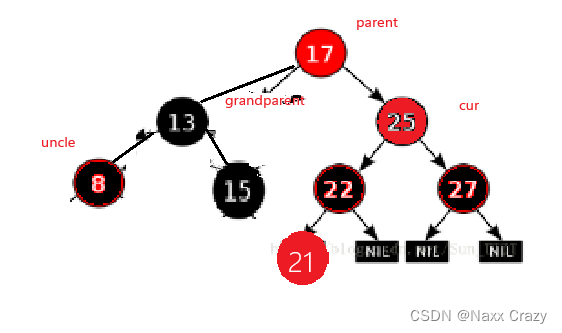
旋转结束后就是这个样子，但是颜色并不符合红黑树，所以我们还需要变色来处理，这种情况下，我们只需要把 grandparent 变为红色，父亲变为黑色：

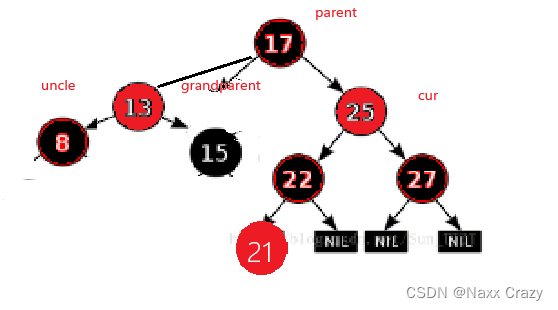
其实叔叔不存在和叔叔存在且为黑色的情况是相同的，如果是单旋的话，那么就是旋转结束后，将付清的颜色变为黑色，然后将祖父的颜色变为红色，如果是双旋的话，那么就是将 cur 的颜色变为黑色，祖父的颜色变为红色。

下面看一下双旋的情况

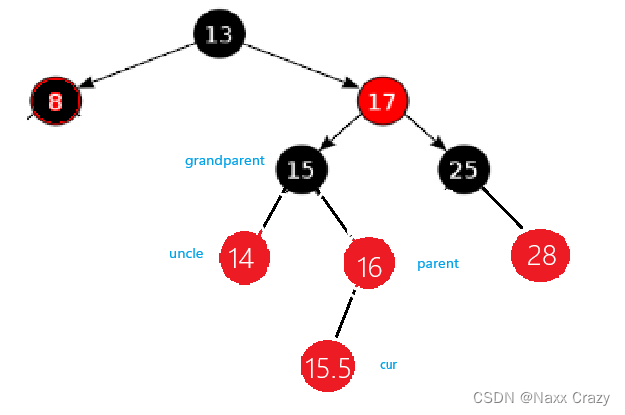
这时候 cur 还是插入的节点，这时候我们跟新一次，然后就可以达到叔叔存在且为黑色，并且还是双旋的情况：

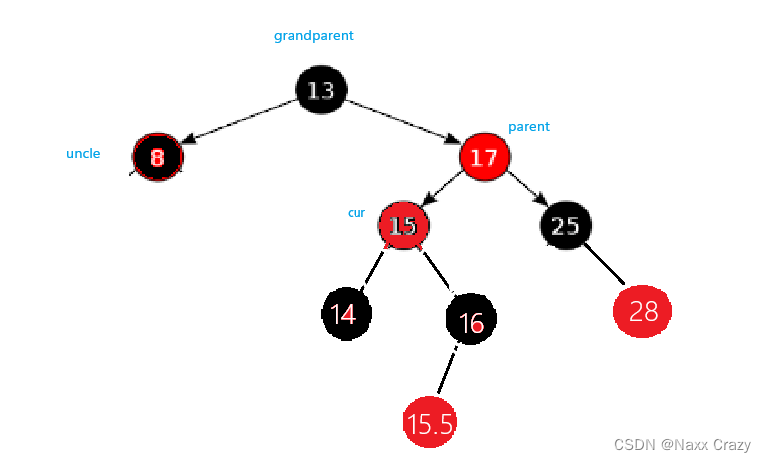此时就是叔叔存在且为黑色，并且我们发现 parent 是grandparent 的右边，cur 是 parent 的左边，所以这里我们使用的是右左双旋：

对 parent 进行右单旋

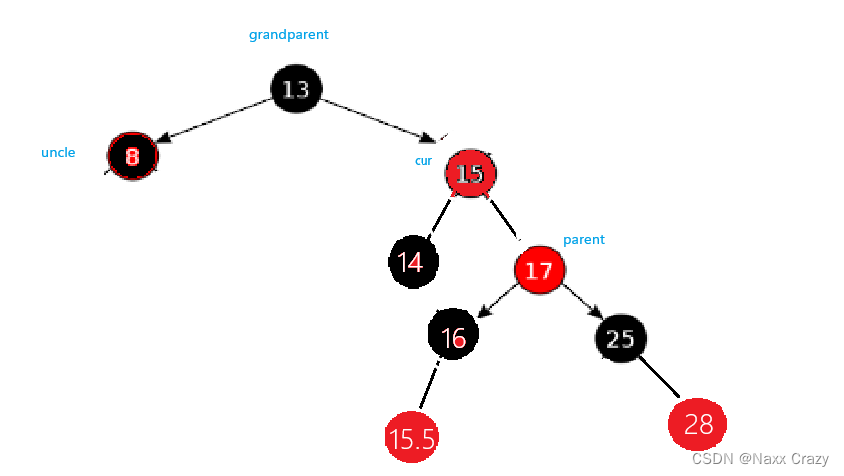
在对 grandparent 使用左单旋转

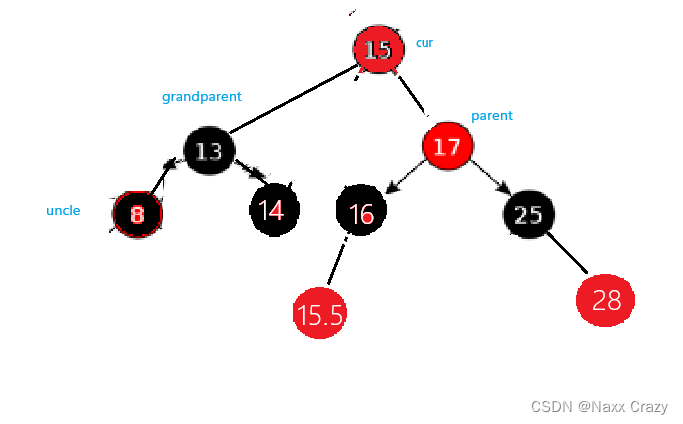
这时候，就是将 grandparent 变为红色，然后将 cur 变为黑色，所以我们在模拟插入后，发现叔叔不存在和存在且为黑的情况是一样的，所以我们后面就可以将叔叔存在且为红色分为一类，和叔叔不存在，或者存在且为黑色，分为一类，将这两类分开处理。

总结

旋转规则上面以及说过了，下面说一下变色：

1. 单旋情况下，将 grandparent 变为红色， parent 变为黑色

2. 双旋情况下，将 grandparent 变为红色， cur 变为黑色

插入实现

节点

红黑树同样是kv结构，所以需要一个存储kv的变量
既然是红黑树，那么除了三叉链，当然还需要一个颜色来控制

enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}
};

插入逻辑

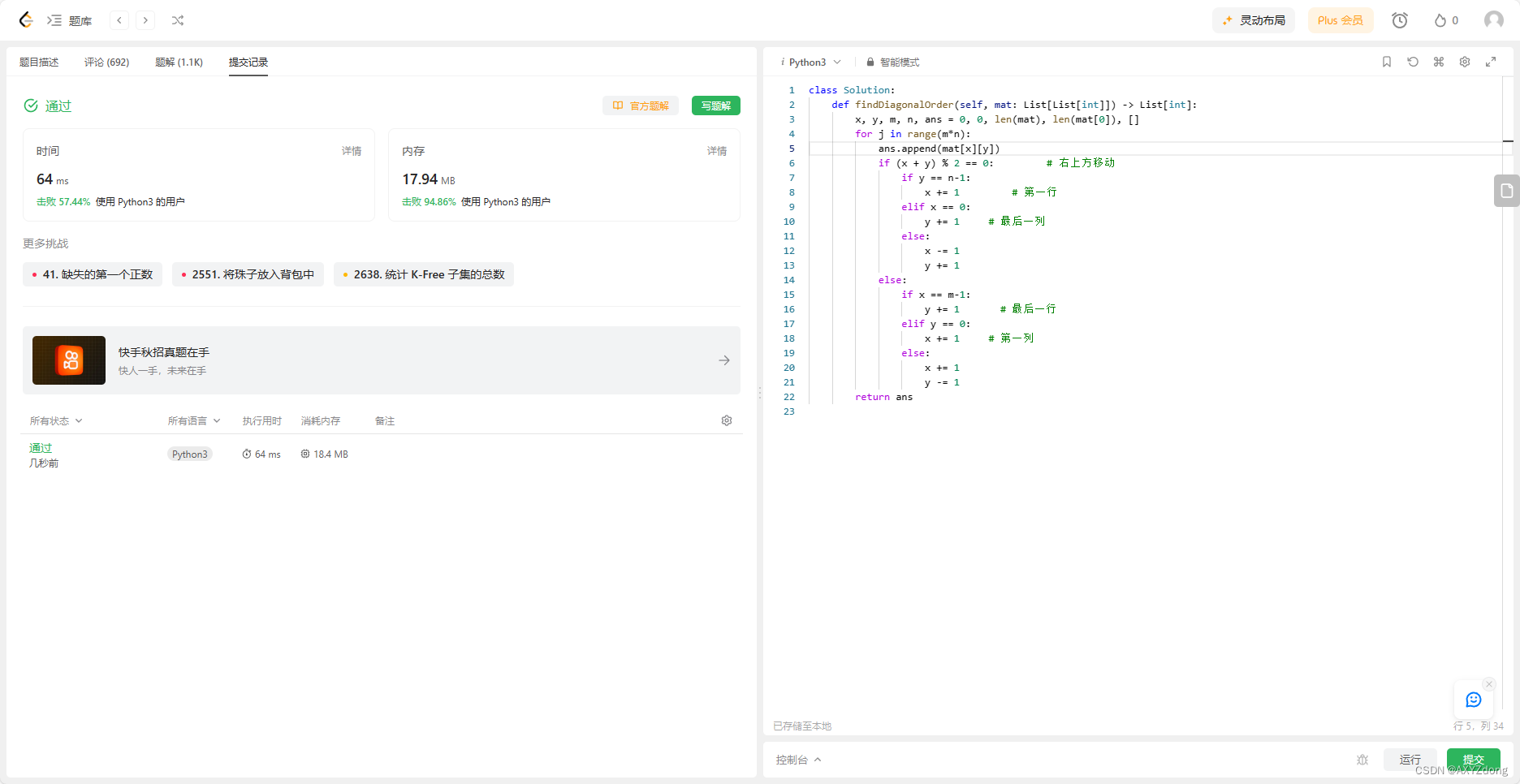
	bool insert(const pair<K, V>& kv){if (_root == nullptr){// 根节点为空，插入到根节点_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root, *parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{// 里面右重复值,插入失败return false;}}// 找到插入位置了cur = new Node(kv);cur->_parent = parent;if (parent->_kv.first < kv.first)parent->_right = cur;elseparent->_left = cur;// 维护红黑树//当父亲不为空，并且父亲的颜色是红色就继续调整while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){// parent 是 grandfather 的左边//       g//    pNode* uncle = grandfather->_right;// 如果叔叔存在，且叔叔的颜色为红色// 那么就将叔叔和父亲的颜色全都改为黑色，然后将祖父的颜色改为红色if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//向上迭代cur = grandfather;parent = cur->_parent;}else{// 叔叔不存在或者叔叔存在但是叔叔的颜色为黑色if (cur == parent->_left){//         g//     p//  c//右单旋RotateR(grandfather);//将父亲的节点变为黑色，祖父的节点变为红色parent->_col = BLACK;grandfather->_col = RED;break;}else{//     g//  p//     c//左右双旋RotateL(parent);RotateR(grandfather);//将cur 的颜色变为黑色，祖父的节点变为红色cur->_col = BLACK;grandfather->_col = RED;break;}}}else{// parent 是 grandfather 的右边//     g//        pNode* uncle = grandfather->_left;// 如果叔叔存在，且叔叔的颜色为红色// 那么就将叔叔和父亲的颜色全都改为黑色，然后将祖父的颜色改为红色if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//向上迭代cur = grandfather;parent = cur->_parent;}else{// 叔叔不存在或者叔叔存在但是叔叔的颜色为黑色if (cur == parent->_right){//    g//       p//          c//左单旋RotateL(grandfather);//将父亲的节点变为黑色，祖父的节点变为红色parent->_col = BLACK;grandfather->_col = RED;break;}else{//       g//           p//       c//右左双旋RotateR(parent);RotateL(grandfather);//将cur 的颜色变为黑色，祖父的节点变为红色cur->_col = BLACK;grandfather->_col = RED;break;}}}}_root->_col = BLACK;return true;}

而旋转，我们以及在 AVL 就以及说过了，树的旋转是搜索树的旋转规则，并不是AVL 树或者红黑树特有的，所以旋转是通用的，只是红黑树的旋转不需要维持平衡因子，只需要旋转即可。

左单旋

	// 左单旋void RotateL(Node* parent){Node* cur = parent->_right;Node* curLeft = cur->_left;parent->_right = curLeft;if (curLeft){curLeft->_parent = parent;}cur->_left = parent;Node* pparent = parent->_parent;parent->_parent = cur;if (pparent == nullptr){// parent 就是根节点_root = cur;cur->_parent = nullptr;}else{if (parent == pparent->_left){pparent->_left = cur;}else{pparent->_right = cur;}cur->_parent = pparent;}}

右单旋

	//右单旋void RotateR(Node* parent){Node* cur = parent->_left;Node* curRight = cur->_right;parent->_left = curRight;if (curRight){curRight->_parent = parent;}cur->_right = parent;Node* pparent = parent->_parent;parent->_parent = cur;if (pparent == nullptr){// 说明 parent 是根节点_root = cur;cur->_parent = nullptr;}else{if (parent == pparent->_left){pparent->_left = cur;}else{pparent->_right = cur;}cur->_parent = pparent;}}