欢~迎~光~临~^_^

目录

1、树的存储结构

1.1双亲表示法

1.2孩子表示法

1.3孩子兄弟表示法

2、树与二叉树的转换

3、树和森林的遍历

3.1树的遍历

3.1.1先根遍历

3.1.2后根遍历

3.2森林的遍历

3.2.1先序遍历森林

3.2.2中序遍历森林

4、树与二叉树的应用

4.1哈夫曼树

4.1.1概念

4.1.2构造哈夫曼树

4.1.3哈夫曼编码

4.1.4C语言实现哈夫曼树

4.2并查集​编辑

4.2.1逻辑结构

4.2.2基本操作

4.2.3存储结构

4.2.4优化

---

1、树的存储结构

 

1.1双亲表示法

树的双亲表示法是一种简单的树结构表示方法，它在每个结点中存储了该结点的父节点信息。具体地，每个结点包含两部分信息，一部分是该结点的数据，另一部分是该结点的父节点的索引值。根结点没有父节点，通常用一个特定的值来表示。双亲表示法的优点是在访问任意结点的父节点时非常快，但是在查找任意结点的子节点时则需要遍历整棵树来确定其子节点。

例如，下面是一个有6个节点的树的双亲表示法的例子： 

struct TreeNode {int data;      // 节点数据int parent;    // 父节点索引
};TreeNode tree[6];   // 定义一个有6个节点的树，每个节点包含数据和父节点索引两部分信息
tree[0].data = 1;   // 第一个节点的数据是1，它是根节点，没有父节点
tree[1].data = 2;   // 第二个节点的数据是2，它的父节点是根节点，其父节点索引为0
tree[1].parent = 0;
tree[2].data = 3;   // 第三个节点的数据是3，它的父节点是根节点，其父节点索引为0
tree[2].parent = 0;
tree[3].data = 4;   // 第四个节点的数据是4，它的父节点是第二个节点，其父节点索引为1
tree[3].parent = 1;
tree[4].data = 5;   // 第五个节点的数据是5，它的父节点是第二个节点，其父节点索引为1
tree[4].parent = 1;
tree[5].data = 6;   // 第六个节点的数据是6，它的父节点是第三个节点，其父节点索引为2
tree[5].parent = 2;

1.2孩子表示法

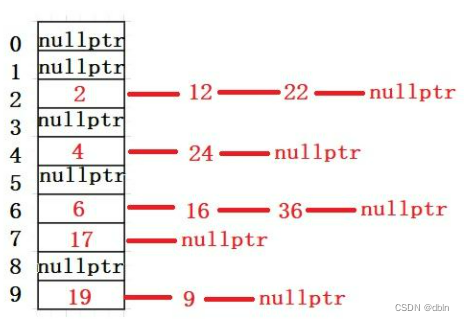
树的孩子表示法是一种常用的树的存储方式，它的基本思想是：每个节点都存储它的孩子节点的指针（地址）。

相比于其他树的存储方式，孩子表示法的优点是：

1. 能够较快地访问节点的孩子节点，因为每个节点都存储了它的孩子节点的指针；

2. 孩子表示法的存储方式相对简单、直观易懂。

但是，孩子表示法也存在一些缺点：

1. 孩子节点的数量不固定，因此存储时需要动态分配内存空间；

2. 访问父节点比较麻烦，需要从根节点开始遍历整棵树才能找到父节点。

1.3孩子兄弟表示法

孩子兄弟表示法是一种树型数据结构中用于表示节点关系的方法，通常用于表示一个树或者一棵森林中的节点之间的关系。

在孩子兄弟表示法中，每个节点包含两个指针：一个指向该节点的第一个孩子节点，另一个指向该节点的下一个兄弟节点。因此，通过这两个指针可以遍历整棵树或森林中的节点，并找到它们的父节点、孩子节点和兄弟节点。

孩子兄弟表示法的主要优点是它能够有效地减少存储空间的使用，因为每个节点只需要存储两个指针，而不需要像其他表示方法那样存储父节点和所有孩子节点的指针。

然而，由于每个节点只存储了两个指针，因此在进行某些操作时，可能需要遍历整棵树或森林，这可能会导致效率较低。

2、树与二叉树的转换

将一棵树转换为二叉树的方法，可以选择先把树转换为森林，然后再对每棵树进行转换。转换的基本思路是：将每个节点的第一个孩子作为其左孩子，将兄弟节点作为其右孩子。

具体实现如下：

1. 首先对树进行先序遍历，从根节点开始遍历。

2. 对于每个节点，如果它有孩子节点，将其第一个孩子节点作为其左孩子。

3. 对于每个节点的兄弟节点，将其作为当前节点右孩子。

4. 对于所有没有孩子节点的节点，将其左孩子和右孩子都设为空。

5. 最终得到的结果是一棵二叉树。

将一棵二叉树转换为一棵树的方法，可以选择先把二叉树转换为森林，然后再将森林中的所有树合并为一棵树。具体实现如下：

1. 针对每个节点，将其左孩子作为其第一个孩子节点，将其右孩子的子树转换为其兄弟节点。

2. 对于每个节点，先将其所有孩子节点合并为一棵子树，然后将其所有兄弟节点依次加入这棵子树中。

3. 最终得到的结果是一棵树。

3、树和森林的遍历

3.1树的遍历

3.1.1先根遍历

树的先根遍历是一种树的遍历方式，先访问根节点，然后依次遍历其子节点，再依次遍历每个子节点的子树的根节点。

 例如，对于下图所示的树：

    A/ \B   C/   / \
D   E   F

先根遍历的顺序是：A -> B -> D -> C -> E -> F。

3.1.2后根遍历

树的后根遍历（也叫后序遍历）是指先访问一个节点的左子树和右子树，最后再访问该节点本身。具体的遍历顺序如下：

1. 访问该节点的左子树
2. 访问该节点的右子树
3. 访问该节点本身

通常，可以使用递归或迭代算法实现树的后根遍历。递归的实现方式比较简单。

迭代的实现方式稍微复杂一些，需要借助栈来实现。具体的算法如下：

1. 将根节点压入栈中
2. 如果栈不为空，则取出栈顶节点
3. 如果该节点没有左右子节点或者其左右子节点已经被访问过，则访问该节点并弹出
4. 如果该节点有左右子节点且其左右子节点还未被访问，则将其右子节点和左子节点依次压入栈中，保证左右子节点先被访问

3.2森林的遍历

3.2.1先序遍历森林

先序遍历森林是指以任意一棵树的根节点为起点，按照先访问根节点，再依次访问子树的方式遍历整个森林。具体操作如下：

1. 访问当前节点
2. 依次以当前节点的子节点为根节点，重复进行上述操作

在实际操作中，可以采用递归或栈的方式实现先序遍历森林。以递归方式为例，实现代码如下：

void preOrderForest(Node* root) {if (root == nullptr) {return;}// 访问当前节点visit(root);// 依次遍历子树for (Node* child : root->children) {preOrderForest(child);}
}

其中，Node代表树节点的数据结构，root表示当前节点，children表示当前节点的子节点列表，visit()表示访问节点的操作。

3.2.2中序遍历森林

森林的后序遍历是将森林中每个树的后序遍历序列依次拼接起来，得到的序列即为森林的后序遍历。

具体步骤如下：

1. 对每棵树分别进行后序遍历。
2. 将每棵树的后序遍历序列依次拼接起来，即可得到森林的后序遍历序列。

例如，对以下森林进行后序遍历：

 B    C     D/ \        / \
E   F      G   H

首先分别对三棵树 B-EF、C、D-GH 进行后序遍历，得到它们的后序遍历序列：

B-EF的后序遍历序列为：E F B

C的后序遍历序列为：C

D-GH的后序遍历序列为：G H D

然后将它们依次拼接起来，得到森林的后序遍历序列：E F B C G H D

4、树与二叉树的应用

4.1哈夫曼树

4.1.1概念

哈夫曼树（Huffman Tree）是一种特殊的二叉树，它是一种最优二叉树，常用于数据压缩和编码中。哈夫曼树的构建过程是基于哈夫曼编码的原理，即将出现频率较高的字符用较短的编码，而出现频率较低的字符用较长的编码。哈夫曼树的构建过程是将每个字符作为一个节点，并将它们按照出现频率从小到大排序，然后将频率最小的两个节点合并成一个新的节点，其权值为两个节点的权值之和。重复这个过程，直到所有节点都被合并成为一个根节点为止。最后形成的这个根节点就是哈夫曼树的根节点。哈夫曼树的叶子节点表示原始数据中的字符，而路径上的0、1代表相应的比特位编码。哈夫曼树是一种满足最优化标准的树形结构，可以使编码后的数据更加紧凑，从而达到压缩数据的目的。

 

4.1.2构造哈夫曼树

哈夫曼树是一种带权路径长度最小的树，用于编码和数据压缩。构造哈夫曼树的过程如下：

1. 将节点按权值从小到大排序，构造n个只含一个节点的二叉树，每个节点代表一个权值。
2. 选择权值最小的两棵二叉树合并成一棵新二叉树，根节点的权值为这两棵二叉树的权值之和。
3. 从已选的n棵二叉树中删除这两棵二叉树，将新的二叉树加入到集合中。
4. 重复步骤2和步骤3，直到只剩下一棵二叉树，这棵树就是哈夫曼树。

4.1.3哈夫曼编码

将字符频次作为字符结点权值，构造哈夫曼树，即可得到哈夫曼编码，可用于数据压缩。

前缀编码：没有一个编码 是另一个编码的前缀

固定长度编码：每个字符用相等长度的二进制位表示

可变长度编码： 允许对不同字符用不等长的二进制位表示

哈夫曼编码的生成过程包括以下几个步骤：

1. 统计每个字符在数据中出现的频率；
2. 将每个字符和其对应的频率构建成一个叶子节点；
3. 构建哈夫曼树，将每个节点按照频率从小到大排序，然后将相邻的两个节点合并成一个新节点，其频率为两个节点的频率之和。重复此过程，直到所有节点都合并为一个根节点；
4. 给每个叶子节点分配一个编码，从根节点开始，向左走则编码为0，向右走则编码为1，直到到达叶子节点；
5. 用每个字符的编码替换原始数据中相应的字符，从而得到压缩后的数据。

4.1.4C语言实现哈夫曼树

哈夫曼树是一种应用广泛的数据结构，用于有效地压缩数据。在C语言中，哈夫曼树的实现可以通过以下步骤完成：

1. 定义节点结构体

首先需要定义一个节点结构体，用于表示哈夫曼树中的每个节点。该结构体包含左子树、右子树、权值和字符等信息。

struct HuffmanNode {int weight;                // 权值char ch;                   // 字符struct HuffmanNode *left;  // 左子树struct HuffmanNode *right; // 右子树
};

2. 定义比较函数

比较函数用于在构建哈夫曼树时对节点进行排序。该函数将根据节点的权值大小进行比较。

int cmp(const void *a, const void *b) {const struct HuffmanNode *node1 = a;const struct HuffmanNode *node2 = b;return node1->weight - node2->weight;
}

3. 构建哈夫曼树

构建哈夫曼树的过程可以通过一些简单的步骤完成。首先需要将每个字符作为一个叶子节点插入到优先队列中，然后不断地取出队列中权值最小的两个节点，将它们合并成一个新节点，并将新节点插入到队列中。重复此过程，直到队列中只剩下一个根节点，此时构建的就是哈夫曼树。

struct HuffmanNode *buildHuffmanTree(const char *str) {// 统计字符出现的次数int count[256] = {0};for (int i = 0; i < strlen(str); i++) {count[str[i]]++;}// 将每个字符作为一个叶子节点插入到优先队列中int size = 0;struct HuffmanNode *nodes[256];for (int i = 0; i < 256; i++) {if (count[i] > 0) {nodes[size] = malloc(sizeof(struct HuffmanNode));nodes[size]->ch = (char)i;nodes[size]->weight = count[i];nodes[size]->left = NULL;nodes[size]->right = NULL;size++;}}// 构建哈夫曼树while (size > 1) {// 取出队列中权值最小的两个节点qsort(nodes, size, sizeof(struct HuffmanNode *), cmp);struct HuffmanNode *left = nodes[0];struct HuffmanNode *right = nodes[1];// 合并两个节点struct HuffmanNode *parent = malloc(sizeof(struct HuffmanNode));parent->ch = '\0';parent->weight = left->weight + right->weight;parent->left = left;parent->right = right;// 将新节点插入到队列中nodes[0] = parent;for (int i = 2; i < size; i++) {nodes[i - 1] = nodes[i];}size--;}return nodes[0];
}

4. 遍历哈夫曼树

遍历哈夫曼树可以得到每个字符的编码，即通过左子树走一步为0，右子树走一步为1。在遍历过程中，需要记录下从根节点到当前节点的路径上的字符编码，以便后续使用。

void traverseHuffmanTree(struct HuffmanNode *node, char *code, int depth) {if (node->left == NULL && node->right == NULL) {// 叶子节点，输出编码printf("%c: %s\n", node->ch, code);} else {// 遍历左子树code[depth] = '0';traverseHuffmanTree(node->left, code, depth + 1);// 遍历右子树code[depth] = '1';traverseHuffmanTree(node->right, code, depth + 1);}
}

5. 完整代码

将以上步骤整合起来，可以得到完整的C语言实现代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>struct HuffmanNode {int weight;                // 权值char ch;                   // 字符struct HuffmanNode *left;  // 左子树struct HuffmanNode *right; // 右子树
};int cmp(const void *a, const void *b) {const struct HuffmanNode *node1 = a;const struct HuffmanNode *node2 = b;return node1->weight - node2->weight;
}struct HuffmanNode *buildHuffmanTree(const char *str) {// 统计字符出现的次数int count[256] = {0};for (int i = 0; i < strlen(str); i++) {count[str[i]]++;}// 将每个字符作为一个叶子节点插入到优先队列中int size = 0;struct HuffmanNode *nodes[256];for (int i = 0; i < 256; i++) {if (count[i] > 0) {nodes[size] = malloc(sizeof(struct HuffmanNode));nodes[size]->ch = (char)i;nodes[size]->weight = count[i];nodes[size]->left = NULL;nodes[size]->right = NULL;size++;}}// 构建哈夫曼树while (size > 1) {// 取出队列中权值最小的两个节点qsort(nodes, size, sizeof(struct HuffmanNode *), cmp);struct HuffmanNode *left = nodes[0];struct HuffmanNode *right = nodes[1];// 合并两个节点struct HuffmanNode *parent = malloc(sizeof(struct HuffmanNode));parent->ch = '\0';parent->weight = left->weight + right->weight;parent->left = left;parent->right = right;// 将新节点插入到队列中nodes[0] = parent;for (int i = 2; i < size; i++) {nodes[i - 1] = nodes[i];}size--;}return nodes[0];
}void traverseHuffmanTree(struct HuffmanNode *node, char *code, int depth) {if (node->left == NULL && node->right == NULL) {// 叶子节点，输出编码printf("%c: %s\n", node->ch, code);} else {// 遍历左子树code[depth] = '0';traverseHuffmanTree(node->left, code, depth + 1);// 遍历右子树code[depth] = '1';traverseHuffmanTree(node->right, code, depth + 1);}
}int main() {char str[] = "hello world";struct HuffmanNode *root = buildHuffmanTree(str);char code[256];traverseHuffmanTree(root, code, 0);return 0;
}

4.2并查集

4.2.1逻辑结构

并查集是一种用于处理集合并、查找和判定两个元素是否在同一集合中的数据结构。它的基本操作有初始化、查找、合并等。

并查集的逻辑结构通常由一个数组和若干个操作函数构成。数组中每个元素对应一个集合，它的值表示当前元素所在集合的根节点编号。在初始化时，每个元素都是一个单独的集合，即它的根节点编号为自身。查找操作用于找到某个元素所在集合的根节点编号，它通过递归查找父节点的方式实现路径压缩。合并操作用于合并两个集合，它将其中一个集合的根节点编号设为另一个集合的根节点编号，从而实现两个集合的合并。

并查集的优点是可以快速地进行集合合并和查找，时间复杂度为O(log n)。它常用于解决连通性问题，如判断图是否连通、求无向图的连通分量等。

4.2.2基本操作

并查集是一种用于维护集合的数据结构，通常支持以下操作：

1. MakeSet(x)：创建一个新的集合，其中只包含元素 x。

2. Union(x, y)：将包含元素 x 和 y 的两个集合合并成一个新集合。

3. Find(x)：查找元素 x 所在的集合，并返回该集合的代表元素。

通常还会有一些额外的操作，例如：

4. SizeOf(x)：返回包含元素 x 的集合中元素的数量。

5. IsConnected(x, y)：判断元素 x 和 y 是否在同一个集合中。

6. CountSets()：返回当前并查集中集合的数量。

在实现并查集的过程中，常见的数据结构有数组和树。使用数组实现时，每个元素的值表示其父节点的索引，根节点的父节点值为-1。使用树实现时，每个节点的父节点指向它的父节点。

在 Find(x) 操作中，可以通过递归或迭代的方式将元素 x 所在的集合中的所有元素都指向该集合的代表元素，以达到路径压缩的效果，加快后续对同一集合的 Find 操作的速度。

在 Union(x, y) 操作中，可以选择将一个集合的根节点作为另一个集合的子树，或者将两个集合的根节点合并成一个新的集合。通常建议采用按秩合并和路径压缩（即将深度较浅的树作为深度较深的树的子树）的算法，以保证并查集操作的时间复杂度为 O(α(n))，其中 α(n) 是反阿克曼函数的逆函数，增长极其缓慢，因此在实际应用中可以认为它是一个常数。

4.2.3存储结构

并查集的存储结构可以采用数组或树形结构。常用的是采用树形结构进行存储。 

对于每个元素x，都有一个对应的父结点parent[x]，如果x是根结点，则parent[x]=-1。在初始化时，可以将每个元素看成一个独立的集合，即其父节点为其自身。随着不断的合并操作，两个元素所在的集合就会合并成为一棵树。

在合并两个集合时，需要将其中一个集合的根节点的父结点设置为另一个集合的根节点。此时，其中一个树就成为另一个树的子树。

通过路径压缩的技巧，可以使得树形结构更加扁平化，从而提高查询效率。具体而言，在查找某个元素所在的集合时，可以沿途将路径上的节点的父节点都设置为该集合的根节点，从而将树的高度降低，进一步提高查询效率。

4.2.4优化

并查集是一种数据结构，用于解决集合的合并和查询问题。在对大量数据进行操作时，为了提高效率，需要对并查集进行优化。

以下是一些并查集的优化方法：

1. 路径压缩：在 find 操作时，将路径上的所有节点都直接连接到根节点上，从而缩短查找路径的长度，减少操作的时间复杂度。

2. 按秩合并：在合并两个集合时，将高度低的集合合并到高度高的集合中，从而保持树的平衡，减少操作的时间复杂度。

3. 路径分裂：在路径压缩时，不仅将路径上的所有节点直接连接到根节点上，还可以将路径上的每个节点的父节点指向其祖先节点的子节点，从而减少路径压缩导致的树的深度增加。

4. 路径减半：在路径压缩时，不仅将路径上的所有节点直接连接到根节点上，还可以将路径上每隔一个节点的父节点指向其祖先节点的父节点，从而减少路径压缩导致的树的深度增加。

🤞❤️🤞❤️🤞❤️树与二叉树的知识点总结就到这里啦，如果对博文还满意的话，劳烦各位看官动动“发财的小手”留下您对博文的赞和对博主的关注吧🤞❤️🤞❤️🤞❤️