1.多叉查找树的效率
- 策略1:m叉查找树中,规定除了根节点外,任何结点至少有[m/2]个分叉,
- 即至少含有[m/2]-1个关键字。
- 策略2:m叉查找树中,规定对于任何一个结点,其所有子树的高度都要相同。
而满足以上两种策略的树被称为B树。
2.B树的定义
B树,又称多路平衡查找树,B树中所有结点的孩子个数的最大值称为B树的阶,通常用m表示。
1.B树的特点
一棵m阶B树或为空树,或为满足如下特性的m叉树:
- 树中每个结点至多有m棵子树,即至多含有m-1个关键字。
- 若根结点不是终端结点,则至少有两棵子树。
- 除根结点外的所有非叶结点至少有「m/2]棵子树,即至少含有「m/2]-1个关键字。
- 所有非叶结点的结构如下:
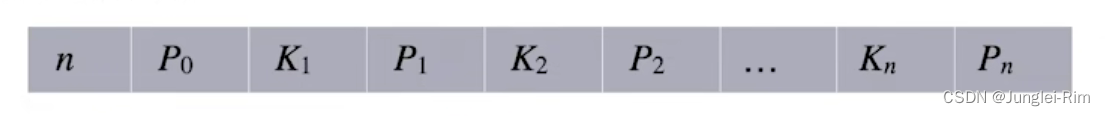
其中,Ki (i = 1,2…, n)为结点的关键字,且满足K1<K2<…<Kn;
Pi (i= 0,1… n)为指向子树根结点的指针,且指针Pi-1所指子树中所有结点的关键字均小于Ki,
Pi所指子树中所有结点的关键字均大于Ki,n( [m/2]- 1≤n≤m -1)为结点中关键字的个数。
- 所有的叶结点都出现在同一层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失败结点,实际上这些结点不存在,指向这些结点的指针为空)。
例如:
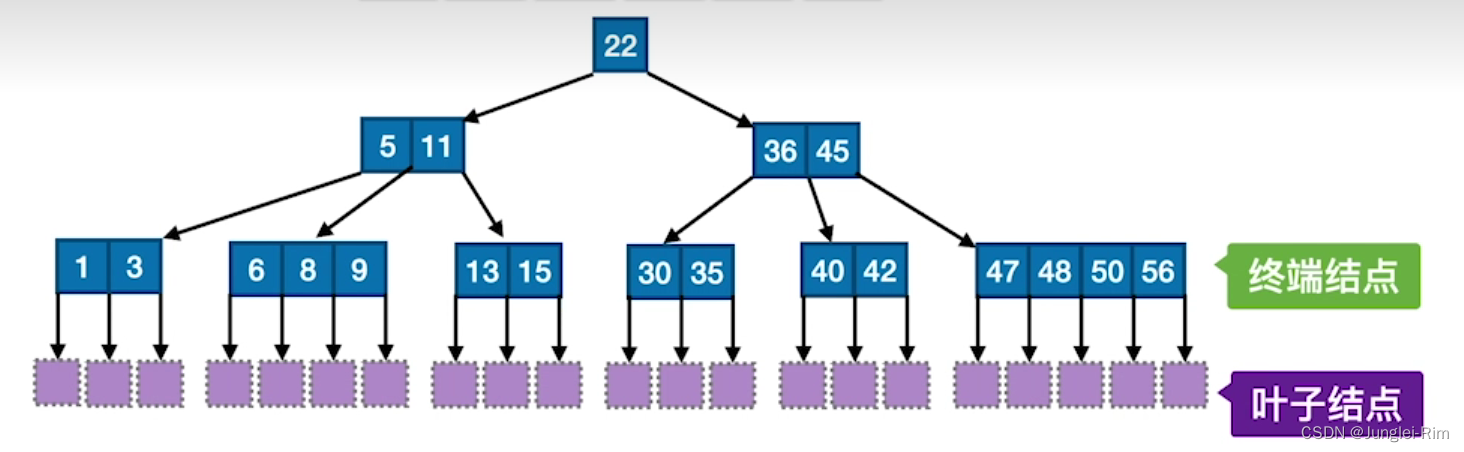
2.m阶B树的核心特性
- 根节点的子树数∈[2, m],关键字数∈[1, m-1]。
- 其他结点的子树数∈[[m/2], m];关键字数∈[[m/2]-1, m-1]
- 对任一结点,其所有子树高度都相同
- 关键字的值∶子树0<关键字1<子树1<关键字2<子树2<…(类比二叉查找树左<中<右)
\
3.计算B树的高度
注:大部分学校算B树的高度不包括叶子结点(失败结点)
问题:含n个关键字的m阶B树,最小高度、最大高度是多少?
1.最小高度:
- 让每个结点尽可能的满,有m-1个关键字,m个分叉,
- 则有 n ≤ ( m − 1 ) ( 1 + m + m 2 + m 3 + . . . + m h − 1 − 1 ) = m h − 1 n≤(m - 1)(1+ m+m^2+m^3+ ...+ m^{h-1}-1)= m ^h-1 n≤(m−1)(1+m+m2+m3+...+mh−1−1)=mh−1,
- 因此 h ≥ l o g m ( n + 1 ) h ≥ log_ m(n+1) h≥logm(n+1)
2.最大高度:
- 让各层的分叉尽可能的少,即根节点只有2个分叉,其他结点只有[m/2]个分叉,
- 各层结点至少有:第一层1、第二层2、第三层2[m/2] …第h层 2 ( [ m / 2 ] ) h − 2 2([m/2])^{h-2} 2([m/2])h−2,
- 第h+1层共有叶子结点(失败结点) 2 ( [ m / 2 ] ) h − 1 2([m/2])^{h-1} 2([m/2])h−1个,
- n个关键字的B树必有n+1个叶子结点,则 n + 1 > 2 ( [ m / 2 ] ) h − 1 n+1> 2([m/2])^{h-1} n+1>2([m/2])h−1,
- 即 h ≤ l o g [ m / 2 ] ( n + 1 ) / 2 + 1 h ≤ log_{[m/2]}{(n+1)/2}+1 h≤log[m/2](n+1)/2+1