Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts

期刊:Expert Systems With Applications SCI1区

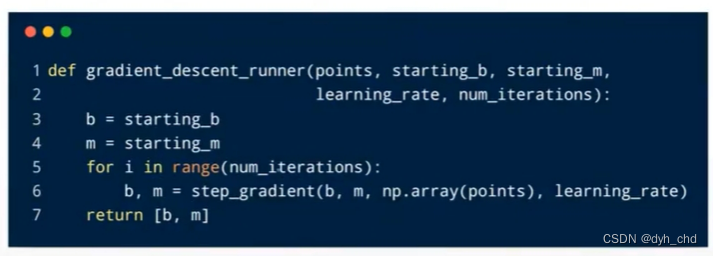
主体框架

    public HGS(){initialize();calculateFitness();sortTheFitness();calculateHungry();for (t = 0;t<T;t++){UpdateWeight();UpdateLocation();calculateFitness();sortTheFitness();calculateHungry();savePoints();}}

ps：经过多次的复现以后，我发现实现一个算法最快的方式就是先将算法分模块搞好，所以上来先贴一个框架图。

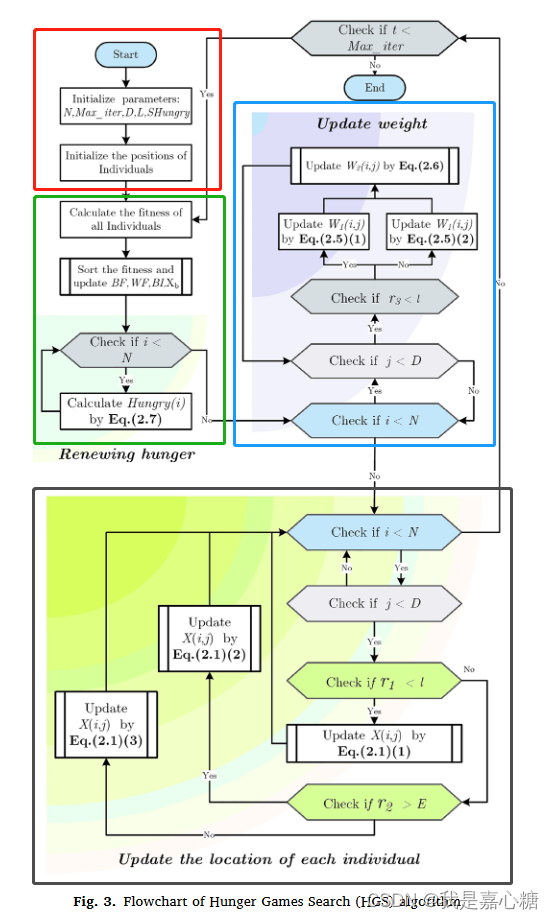
这篇论文主要分为四个模块，分别是初始化模块，适应度与饥饿值设置模块，权重更新模块，位置更新模块。

论文有意思的点：

在这篇文章里面的公式非常的多，但是在这里我只想着重介绍这篇论文的创新点：饥饿机制。

文章定义了一个叫饥饿值的东西，如下公式所示。我们发现当且仅当i适应度值最小的时候，饥饿值为0，别的情况饥饿值为上次的饥饿值加上H。也就是说，只要适应度高，那么就会越来越饥饥饿。后面我们再说这个饥饿度怎么用。值得注意的是：每一轮迭代都会更新一次hungry值

$$\text{ hungry }(i)=\{\begin{array}{c}0,\text{ AllFitness }(i)==BF\\ \text{ hungry }(i)+H,\text{ AllFitness }(i)!=BF\end{array}$$

其中$BF$为最差的适应度，也就是最小的适应度值。$H$的定义如下所示

$$\begin{array}{rl}& TH=\frac{F(i)-BF}{WF-BF}\times r_6\times 2\times (UB-LB)\\ & H=\{\begin{array}{c}LH\times (1+r),TH<LH\\ TH,TH\ge LH\end{array}\end{array}$$

其中$F(i)$为适应度值，$WF$(Worse Fitness)为最大的适应度值（至今为止），$UB和LB$为问题空间的上下界。$LH$(Limit Hungry)则为饥饿感的下限，r是一个随机值。

也就是说当适应度值$F(i)$越小的时候，$TH$（Temp Hungry）会越小，当低于上限的时候，本轮增加的饥饿度$H$，将会被设置为大于$TH$的一个随机值。

我们从上面的三个公式只要知道一个关键结论就好了：

适应度越小，越不饥饿。

适应度越大，这轮增加的饥饿度越高。

那么这个饥饿度值该怎么用呢？

$$\overrightarrow{W_1(i)}=\{\begin{array}{c}\text{ hungry }(i)\cdot \frac{N}{\text{ SHungry }}\times r_4,r_3<l\\ 1，r_3>l\end{array}$$

$$\overrightarrow{W_2(i)}=(1-\exp (-\mid \text{ hungry }(i)-\text{ SHungry }\mid ))\times r_5\times 2$$

论文构建了两个向量，分别是$W_1(i),W_2(i)$，这两个向量负责对个体进行变异，这里最关键的点是$SHungry$，这是所有$hungry$的总和，我们可以发现，两个向量组的规律。

对于$W_1(i)$而言，hungry越小，里面的值越小

对于$W_2(i)$而言，hungry越小，里面的值越接近2也就是说里面的值越大。

$$\overrightarrow{X(t+1)}=\{\begin{array}{c}{\text{ Game }}_1:\overrightarrow{X(t)}\cdot (1+\mathrm{randn}(1)),r_1<l\\ {\text{ Game }}_2:\overrightarrow{W_1}\cdot \overrightarrow{X_b}+\vec{R}\cdot \overrightarrow{W_2}\cdot \left|\overrightarrow{X_b}-\overrightarrow{X(t)}\right|,r_1>l,r_2>E\\ {\text{ Game }}_3:\overrightarrow{W_1}\cdot \overrightarrow{X_b}-\vec{R}\cdot \overrightarrow{W_2}\cdot \left|\overrightarrow{X_b}-\overrightarrow{X(t)}\right|,r_1>l,r_2<E\end{array}$$

最后，每轮迭代的时候都根据上面的公式对位置进行变换，在文中，l被设置为0.08，在公式1中，其实就是一个高斯变异，烟花算法也用到这个。

公式二和三，本质上是一个DE，差分进化的两个公式都是没头脑的，就算正向学习和反向学习，很多论文也有这个。最后还有个E，这个E也是作者自己设定的一个阈值，可以参照野狗群算法，不过作者将这个搜索阈值自己自定义了：

$$E=\mathrm{sech}(|F(i)-BF|)$$

$$\left(\mathrm{sech}(x)=\frac{2}{e^x+e^{-x}}\right)$$

sech就是双曲正割函数

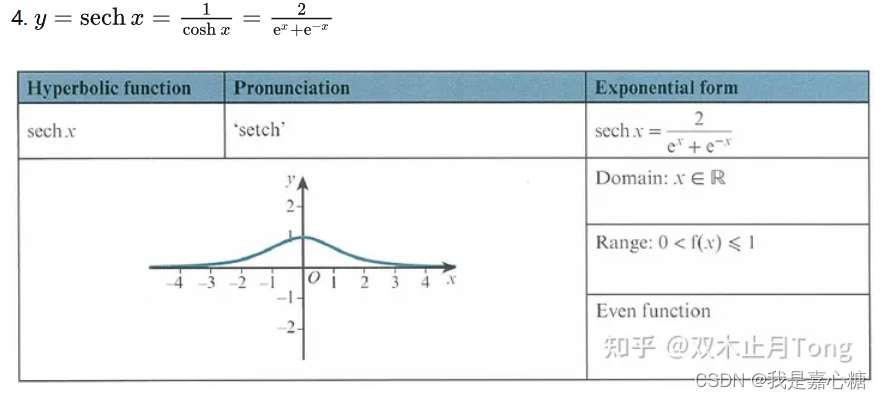
x越大，y越小，也就是说，当前解的适应度值越小，E就会越接近1，公式3被调用的概率就会变高。当前的解适应度越大，E就会越接近0，公式2被调用的概率越大。

最后再补充一个

$$\begin{array}{rl}& \vec{R}=2\times \text{ shrink }\times \text{ rand }-\text{ shrink }\\ & \text{ shrink }=2\times \left(1-\frac{t}{T}\right)\end{array}$$

这个东西就是随着迭代次数，波动逐渐减少的向量，最后会收敛到0，值得注意的是R里面是有正有负的，意味着game2和game3是存在等效的情况。

实验的截图~

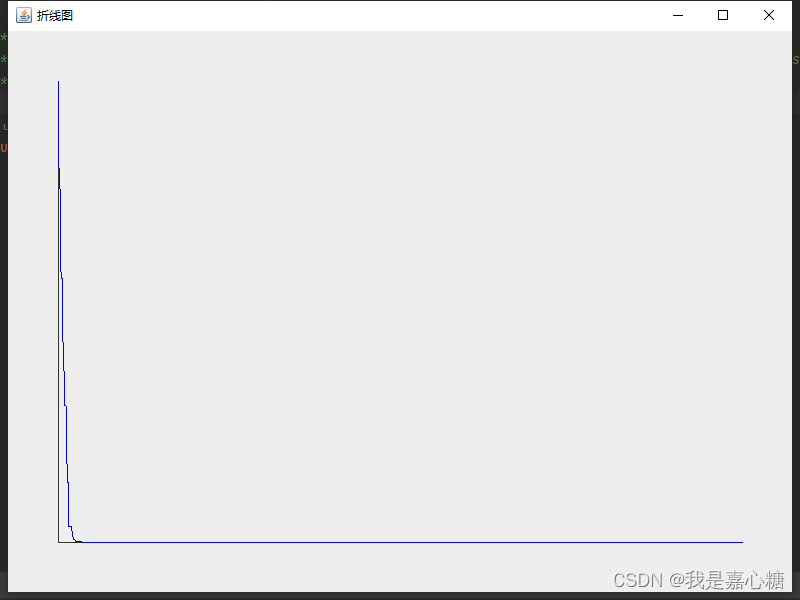
寻找sphere最小值。

实际代码

import javax.swing.*;
import java.awt.*;
import java.util.*;
import java.util.List;
import java.util.function.Consumer;/*** Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts*/public class HGS {int N = 30;//5 10 30 50 100Double D;Double L = 0.08;Double H;Double SHungry;List<Double> Xb;double BF = Double.MAX_VALUE;double WF = -Double.MAX_VALUE;double lb = 0;double ub = 1;int dimension = 30;int t;int T = 1000;List<Double> R = new ArrayList<>(dimension);ArrayList<Point> res = new ArrayList<>();double LH = 10000;public HGS(){initialize();calculateFitness();sortTheFitness();calculateHungry();for (t = 0;t<T;t++){UpdateWeight();UpdateLocation();calculateFitness();sortTheFitness();calculateHungry();savePoints();}}public static void main(String[] args) {HGS hgs = new HGS();ArrayList<Point> points = hgs.res;// 创建绘制折线图的窗口JFrame frame = new JFrame("折线图");frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);frame.add(new LineChart(points));frame.setSize(800, 600);frame.setLocationRelativeTo(null);frame.setVisible(true);}public void savePoints(){System.out.println("curt:"+t+",BF="+BF);res.add(new Point(t,(int)(BF*100000)));}List<Individual> individuals = new ArrayList<>();public void initialize(){IndividualFactory individualFactory = new IndividualFactory(dimension,lb,ub);individuals = individualFactory.getRandomIndividuals(N);t = 0;}public void calculateFitness(){for (Individual i:individuals) {i.UpDateFitness();}}public void sortTheFitness(){individuals.sort((a,b)->new Double(a.fitness).compareTo(b.fitness));//按照适应度排序WF = Math.max(WF,individuals.get(N-1).fitness);if(BF>individuals.get(0).fitness){BF = individuals.get(0).fitness;Xb = new ArrayList<>(individuals.get(0).position);//copy一份}BF = Math.min(BF,individuals.get(0).fitness);}public void calculateHungry(){for (Individual i:individuals) {if(i.fitness==BF){i.hungry = 0;}else {double r6 = Math.random();Double TH = (i.fitness-BF)/(WF-BF)*r6*2*(ub-lb);Double H;if(TH<LH){H = LH*(1+Math.random());}else {H = TH;}i.hungry = i.hungry+H;}}}public void UpdateWeight(){double SHungry = 0;for (Individual i:individuals) {SHungry+=i.hungry;}for (Individual i:individuals) {i.updateW(N,SHungry,L);}}public void UpdateLocation(){for (Individual i:individuals) {i.upDateLocation(L,t,T,Xb,BF);}}
}class Individual{double hungry;double fitness;double lb;double ub;List<Double> position = new ArrayList<>();List<Double> w1;List<Double> w2;int dimension;public double getHungry() {return hungry;}public void setHungry(double hungry) {this.hungry = hungry;}public Individual(double lb, double ub, List<Double> position) {this.lb = lb;this.ub = ub;this.position = position;dimension = position.size();w1 = new ArrayList<>(dimension);w2 = new ArrayList<>(dimension);for (int i = 0; i < dimension; i++) {w1.add(0.0);w2.add(0.0);}}public void Game1(){//formula 2.1Random random = new Random();for (int i = 0; i < dimension; i++) {double originX = position.get(i);position.set(i,originX*(1+random.nextGaussian()));}}public void Game2(List<Double> R,List<Double> Xb){//formula 2.1for (int i = 0; i < dimension; i++) {position.set(i,w1.get(i)*Xb.get(i)+R.get(i)*w2.get(i)*Math.abs(Xb.get(i)-this.position.get(i)));}}public void Game3(List<Double> R,List<Double> Xb){//formula 2.1for (int i = 0; i < dimension; i++) {position.set(i,w1.get(i)*Xb.get(i)-R.get(i)*w2.get(i)*Math.abs(Xb.get(i)-this.position.get(i)));}}public void upDateLocation(double l,int t,int T,List<Double> Xb,double BF){double r1 = Math.random();double r2 = Math.random();if(r1<l){Game1();}else{List<Double> R = new ArrayList<>(dimension);for (int i = 0; i < dimension; i++) {R.add(0.0);}double shrink = 2.0*(1.0-t/T);for (int i = 0; i < dimension; i++) {R.set(i,2*shrink*Math.random()-shrink);}double E = sech(Math.abs(fitness-BF));if(r2>E){Game2(R,Xb);}else {Game3(R,Xb);}}}public static double sech(double x){return 2.0/(Math.exp(x)+Math.exp(-x));}public void updateW(int N,double SHungry,double l){for (int i = 0; i < dimension; i++) {//formula 2.6double r3 = Math.random();double r4 = Math.random();if (r3<l){w1.set(i,hungry*N/SHungry*r4);}else {w1.set(i,1.0);}double r5 = Math.random();//formula 2.6w2.set(i,(1-Math.exp(-Math.abs(hungry-SHungry)))*r5*2);}}public void UpDateFitness(){this.fitness = Sphere(this.position);}public static double Sphere(List<Double> x){double sum = 0;for (int i = 0; i < x.size(); i++) {sum += x.get(i)*x.get(i);}return sum;//修正函数}
}
class IndividualFactory{Random random = new Random();private int dimension;private double lb;private double ub;public IndividualFactory(int dimension,double lb,double ub){this.dimension = dimension;this.lb = lb;this.ub = ub;}public Individual getRandom(){List<Double> Position = new ArrayList<>(dimension);for (int i = 0; i < dimension; i++) {Position.add(lb+(ub-lb)*random.nextDouble());}Individual individual = new Individual(lb,ub,Position);individual.UpDateFitness();return individual;}public List<Individual> getRandomIndividuals(int N){List<Individual> individuals = new ArrayList<>(N);for (int i = 0; i < N; i++) {individuals.add(getRandom());}return individuals;}}
class LineChart extends JPanel {private ArrayList<Point> points;public LineChart(ArrayList<Point> points) {this.points = points;}@Overrideprotected void paintComponent(Graphics g) {super.paintComponent(g);Graphics2D g2d = (Graphics2D) g;int margin = 50; // 留出一些边距int width = getWidth() - 2 * margin;int height = getHeight() - 2 * margin;// 绘制坐标轴g2d.drawLine(margin, margin, margin, margin + height); // 垂直轴g2d.drawLine(margin, margin + height, margin + width, margin + height); // 水平轴// 计算最大和最小的x和y值int minX = Integer.MAX_VALUE, minY = Integer.MAX_VALUE;int maxX = Integer.MIN_VALUE, maxY = Integer.MIN_VALUE;for (Point point : points) {if (point.x < minX) minX = point.x;if (point.x > maxX) maxX = point.x;if (point.y < minY) minY = point.y;if (point.y > maxY) maxY = point.y;}// 绘制折线g2d.setColor(Color.BLUE);for (int i = 0; i < points.size() - 1; i++) {int x1 = margin + (points.get(i).x - minX) * width / (maxX - minX);int y1 = margin + height - (points.get(i).y - minY) * height / (maxY - minY);int x2 = margin + (points.get(i + 1).x - minX) * width / (maxX - minX);int y2 = margin + height - (points.get(i + 1).y - minY) * height / (maxY - minY);g2d.drawLine(x1, y1, x2, y2);}}}