目录

一.基本理论

 二.两类相关系数的对比

三.相关系数的假设检验

四.MATLAB的相关操作

五.其他有关的一些列技巧

六.案例展示

七.实战操作

---

一.基本理论

所谓相关系数，本质上是来衡量两组数据的关系大小——对应呈现函数关心的两种变量，那么我们可以很清楚他们之间的关系；而对于没有强烈关联的变量，我们若无法抽象他们之间的函数，那么可以用相关性强弱来描述他们之间的关系所在。

如上是有关相关系数的计算方式：所谓的皮尔逊相关系数，即为我们本科期间学过的那种，也就是考研数一数三会涉及的部分~

如下是需要注意的一些列理论知识：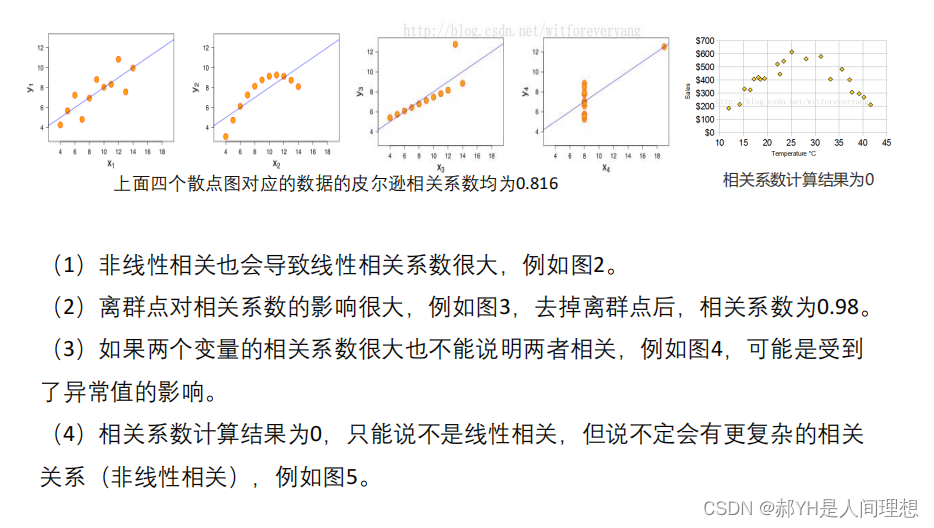
 总的来说，当变量之间呈现线性关系时，才有考虑相关系数大小的意义~

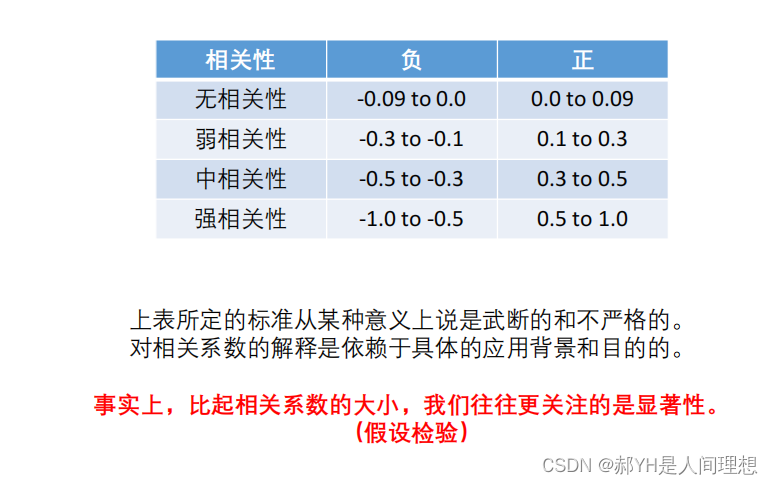
如上是衡量相关性强弱的普遍标准：一般认为相关系数大于0.5时，呈现较强的相关性~

 二.两类相关系数的对比

通常我们会接触到皮尔逊相关系数和斯皮尔曼相关系数两种类型。

如下是关于斯皮尔曼相关系数的理论：

 如下是区别方式：

三.相关系数的假设检验

这一部分非常理论，考数一的同学可以稍微研究研究，不过还是以实际操作为重点~ 

 

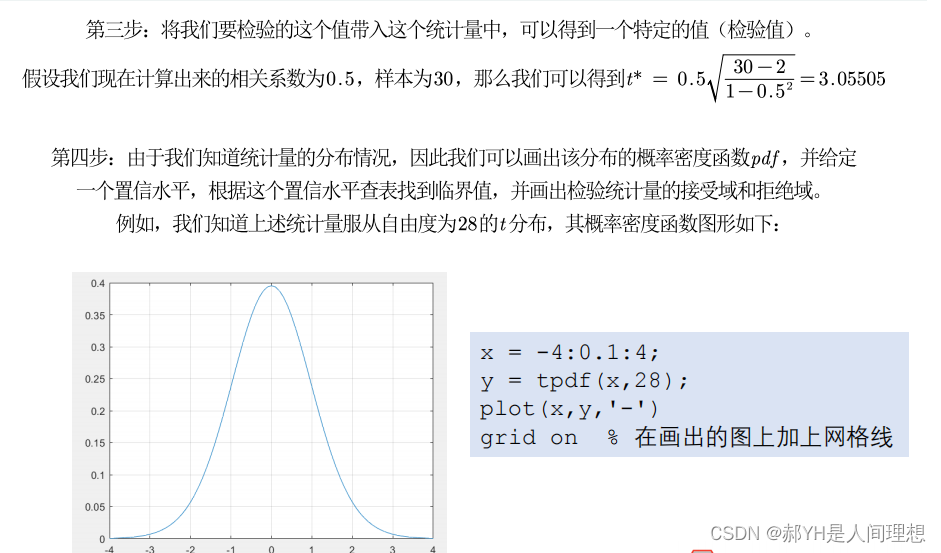
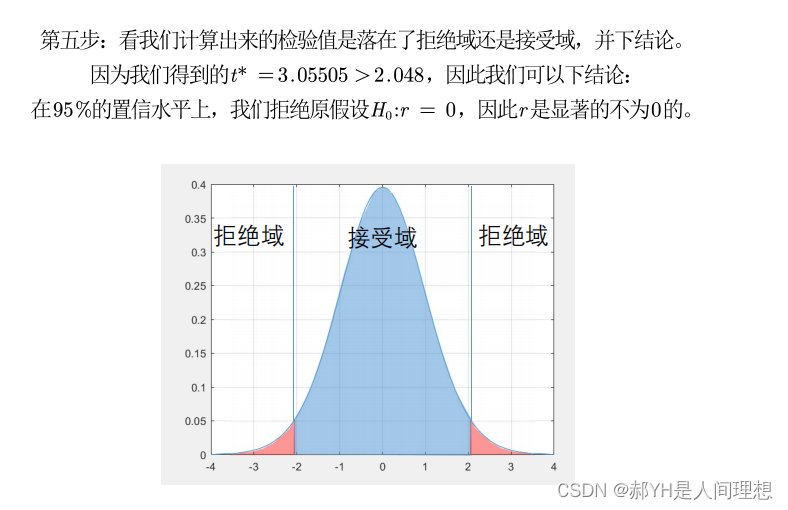
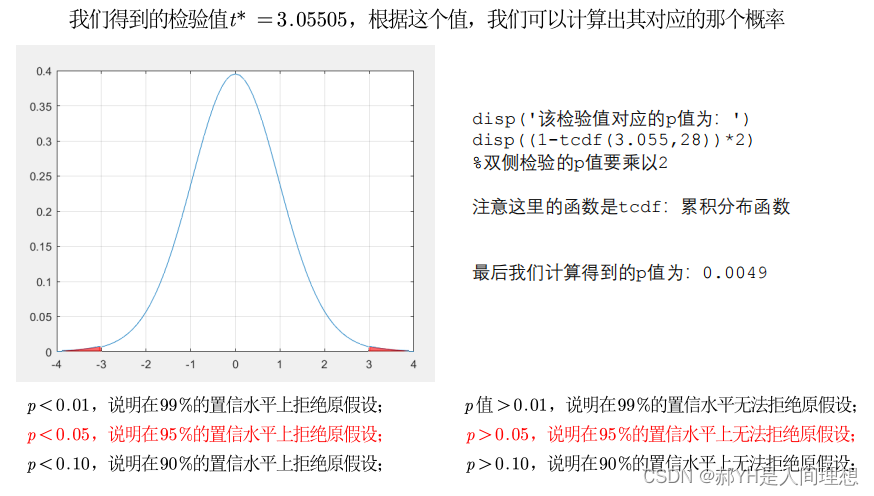
满足假设检验的条件：

第一， 实验数据通常假设是成对的来自于正态分布的总体。 因为我们在求皮尔

逊相关性系数以后，通常还会用 t 检验之类的方法来进行皮尔逊相关性系数检验，

而 t 检验是基于数据呈正态分布的假设的。

第二， 实验数据之间的差距不能太大。 皮尔逊相关性系数受异常值的影响比较

大。

第三：每组样本之间是独立抽样的。 构造 t 统计量时需要用到。

四.MATLAB的相关操作

如下是20个初二学生的身高及跳远成绩：

身高	立定跳远
163	208
158	210
157	210
158	210
157	210
170	198
167	180
160	187
167	180
160	187
170	198
160	167
165	190
162	175
166	200
169	179
159	217
162	175
166	200

首先介绍一些基本的统计函数：

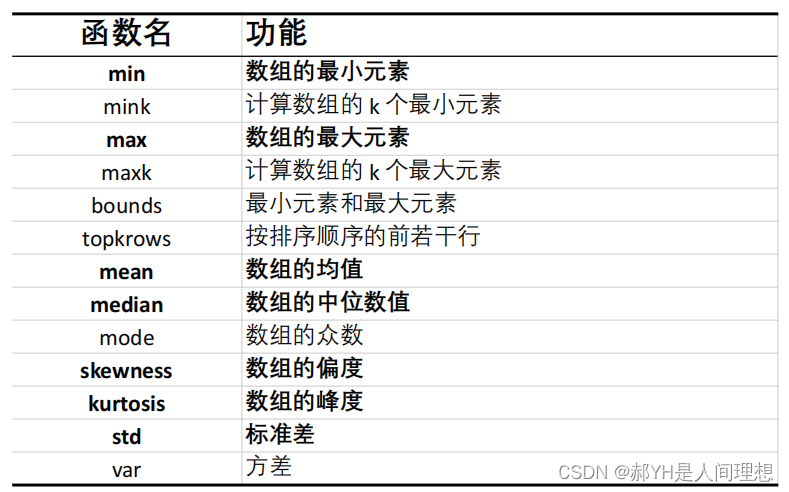
如下是计算皮尔逊相关系数的代码：

x=[163,158,157,158,157,170,167,160,167,160,170,160,165,162,166,169,159,162,166];
y=[208,210,210,210,210,198,180,187,180,187,198,167,190,175,200,179,217,175,200];
R=corrcoef(x,y);

如下代码会返回假设检验要用到的p值：

[R,P]=corrcoef(x,y);

 如下是正态分布检验用到的代码：

%% 正态分布检验
[hx,px] = jbtest(x,0.05);
[hy,py] = jbtest(y,0.05);
disp(H)
disp(P)

如下是计算斯皮尔曼相关系数的代码（通常情况下两种相关系数不一样大）：

（注意：x与y必须是列向量）

Rs=corr(x',y','type','Spearman');

 斯皮尔曼相关系数假设检验的公式：

test=(1-normcdf(Rs*(19-1)^1/2))*2;

test值>0.05即无法拒绝原假设。

如上即为操作的基本功。

五.其他有关的一些列技巧

相关技术等统计学问题，用SPSS计算往往更方便，如下图：

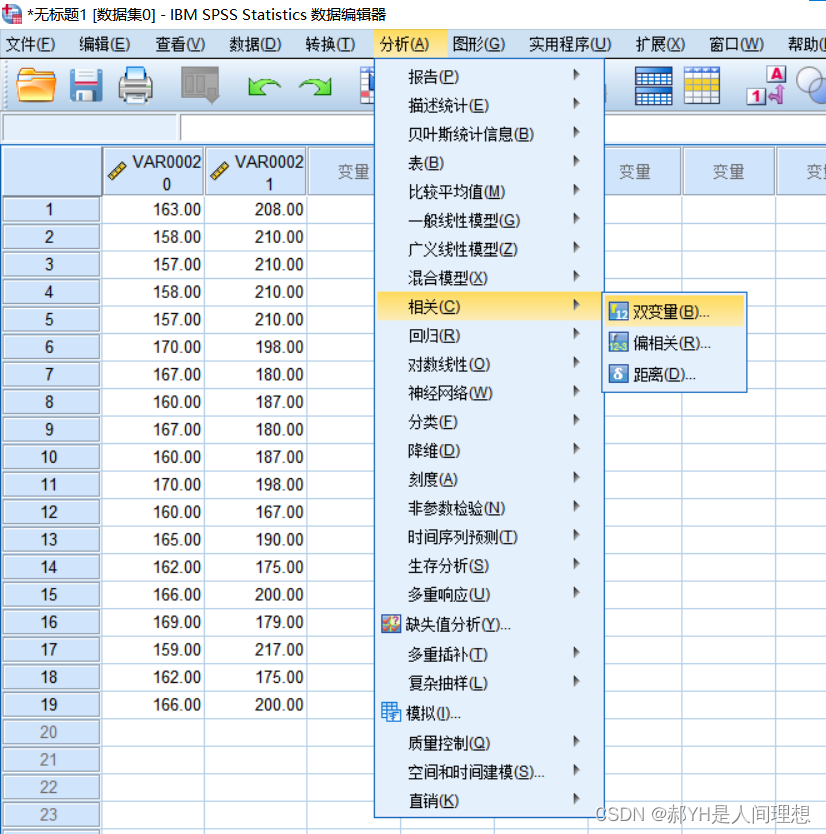
勾选自己想要的选项：

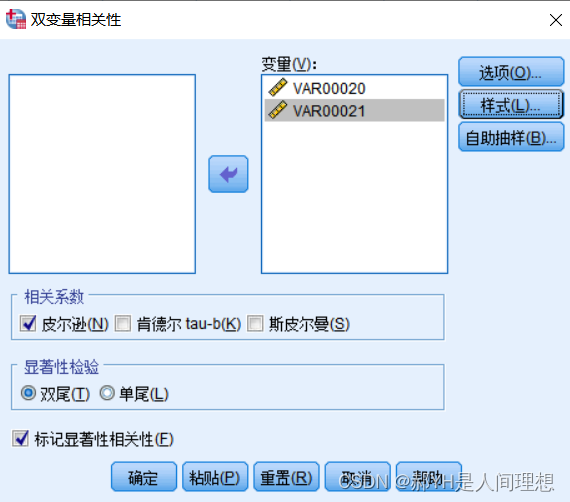
 计算结果如下：

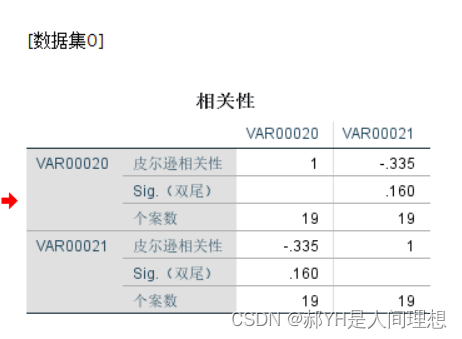
此外，关于热力图的画法，MATLAB种用到函数heatmap(R)，其中R即为相关系数矩阵。 

此处介绍一种更投机的操作方式——Excel法：

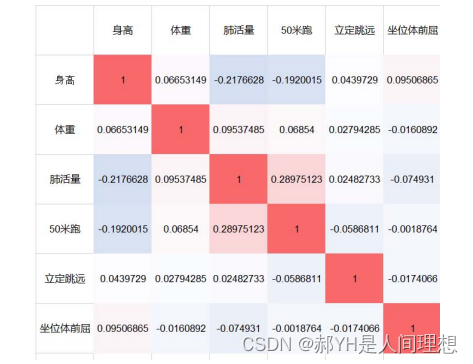
具体的方式就是，把相关系数矩阵沾进Excel中，再将行列大小调成一致——成正方形显示~再根据条件格式设置样式~

六.案例展示

分享在数模和市场调研大赛中用到相关性分析的典例：

 21年亚太赛的案例，当时第一次纯小白，画得属实抽象.........

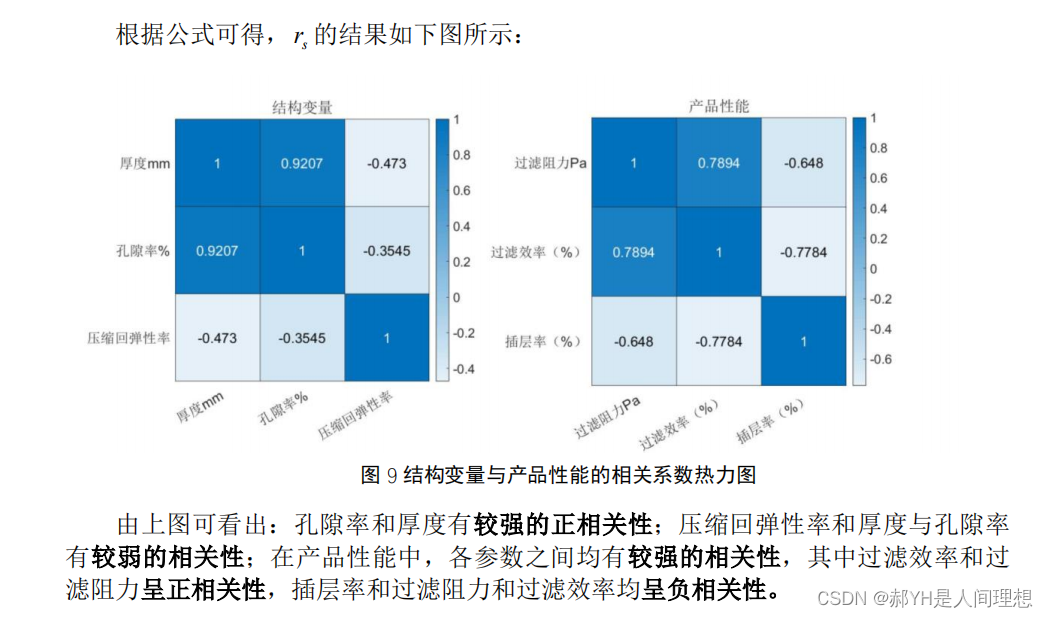 22年华数杯，有进步

22国赛选拔赛，渐入佳境

 

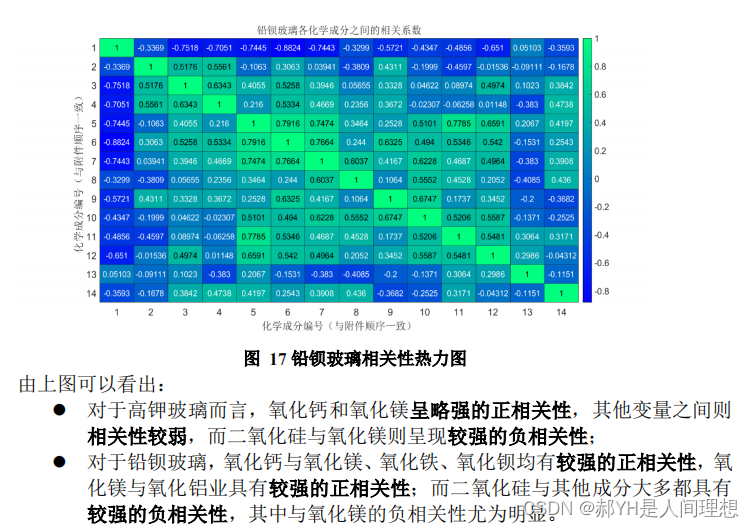
 22年国赛，养兵千日用兵一时（写得有点问题，不重要。。。当时已经交了才发现错误）

 

23年正大杯——这种就是前文提到的Excel法，属实有点low哈哈哈，平时小打小闹无所谓，学术论文尽量还是正经画比较好~ 

七.实战操作

来做一个实战：很多小伙伴都会关心——考研时名校会不会对本科出生比较有成见呢？我们采用23年WHU电子信息专硕的录取情况来做一个统计~

我们计算4组相关系数：

• 初试成绩与本科出生
• 复试成绩与本科出生
• 初试成绩与录取情况
• 出生与录取情况

其中，我们对本科出生做出如下正向化——即学校越好得分得分越高：

学校类型	对应数值
武汉985	4
其他区域985	3
211	2
双非及以下	1

而是否拟录取使用1和0分别标记。

注意：实际上，处理0-1变量，更适合使用Logistic回归，不过这里为了说明相关性分析的主要思想就凑合用了...

最后得到如下118条数据：

序号	初试得分	复试得分	出生	录取情况
1	428	88.72	4	1
2	414	89.04	3	1
3	423	86.12	3	1
4	405	91.08	2	1
5	396	91.28	4	1
6	412	86.12	2	1
7	401	89.32	1	1
8	402	88.88	4	1
9	403	87.92	3	1
10	426	80.08	4	1
11	421	80.6	1	1
12	403	84.68	4	1
13	396	86.36	4	1
14	377	91.32	4	1
15	412	80.8	1	1
16	401	84	3	1
17	392	86	1	1
18	394	84.72	4	1
19	384	87.16	2	1
20	402	81.4	3	1
21	391	84.68	4	1
22	384	86.68	2	1
23	387	85.28	3	1
24	385	85.64	4	1
25	392	83.32	3	1
26	409	77.16	3	1
27	370	88.68	2	1
28	393	81.52	2	1
29	402	78.76	3	1
30	371	87.8	4	1
31	363	89.88	2	1
32	371	87.4	1	1
33	363	89.64	4	1
34	356	91.64	1	1
35	370	87.36	2	1
36	361	89.72	4	1
37	394	79.76	1	1
38	374	85.48	2	1
39	377	84.36	1	1
40	360	89.4	2	1
41	380	83.36	2	1
42	377	84.24	2	1
43	388	80.92	3	1
44	360	89.32	3	1
45	389	80.44	2	1
46	364	87.88	4	1
47	368	86.04	1	1
48	388	79.84	2	1
49	356	89.4	4	1
50	381	81.8	3	1
51	374	83.36	3	1
52	371	84.2	4	1
53	383	80.6	1	1
54	369	84.76	1	1
55	367	85.32	2	1
56	386	79.4	4	1
57	377	81.48	3	1
58	359	86.88	1	1
59	376	81.64	2	1
60	371	83.12	4	1
61	376	81.32	3	1
62	375	81.6	1	1
63	355	87.48	1	1
64	375	81.24	3	1
65	361	85.32	3	1
66	361	85.04	2	1
67	369	82.6	3	1
68	365	83.64	2	1
69	358	85.56	1	1
70	369	81.8	2	1
71	372	80.88	3	1
72	364	83.24	1	1
73	365	82.68	1	1
74	366	82.36	2	1
75	359	84.12	2	1
76	372	80.12	4	1
77	365	81.96	4	1
78	359	83.72	1	1
79	357	84.2	1	1
80	363	81.72	1	1
81	366	80.56	2	1
82	355	83.64	1	1
83	356	83.32	2	1
84	383	75.08	2	1
85	373	78.04	1	1
86	372	78.32	2	1
87	360	81.88	2	1
88	385	74.28	4	0
89	357	81.92	2	0
90	392	71.4	2	0
91	365	79.12	1	0
92	361	79.48	2	0
93	378	74.2	1	0
94	380	73.28	1	0
95	370	76.16	3	0
96	359	79.4	1	0
97	371	75.44	4	0
98	359	78.32	1	0
99	367	75.68	2	0
100	357	78.2	4	0
101	361	76.48	1	0
102	362	75.6	1	0
103	394	65.56	2	0
104	394	65.52	1	0
105	387	67.56	1	0
106	377	70.16	2	0
107	370	71.8	2	0
108	359	74.8	1	0
109	361	73.56	2	0
110	362	73.2	2	0
111	358	73.96	1	0
112	358	73.88	2	0
113	355	74.4	2	0
114	368	69.32	2	0
115	355	71.96	3	0
116	356	70.88	1	0
117	367	61.52	1	0
118	360	63.08	1	0

直接用MATLAB一个corrcoef搞定，结果如下：

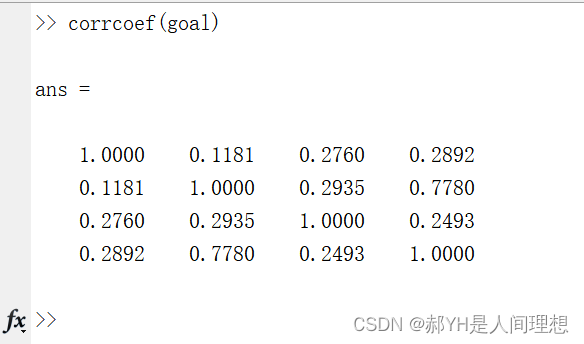
因此得出如下相关系数的结果：

• 初试成绩与本科出生：0.2760
• 复试成绩与本科出生：0.2935
• 初试成绩与录取情况：0.2892
• 出生与录取情况：0.2493

---

综上，我们可以得出结论：

首先，初试成绩与本科出生的相关性较低，这现实逻辑相一致——初试成绩仅与过去一年你的投入时间成本呈强烈正相关，而与别的面板数据——比如绩点等，没有太大的关系；

此外，复试成绩与本科出生并没有很强的相关性，证明该校不歧视本科出生；

初试成绩与录取情况虽然成较弱的正相关，可能有两个原因——一是模型的严谨性不足，另一方面可能是因为初试成绩占比相对较低（巧合的是复试强相关......），这要不同学校具体分析；

最后，出生与录取情况呈弱相关，说明上岸与否，全掌握在自己手里。

• 天助自助者，望诸君共勉~