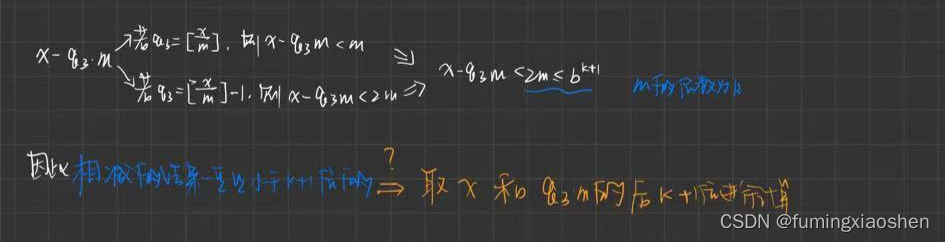Barrett reduction
约减概述
约减的定义(reduction): z ( m o d p ) z \pmod p z(modp)
优化约减的目的:取模操作的底层实现往往使用到的是除法,而除法操作往往是较为耗时的,因此需要把除法操作替换为不那么费时的其他操作。
Barrett 约减概述
单模数多约减:多个约减操作,其模数 p p p是固定的,而 z z z不同。
针对单模数多约减的情况,可以使用Barrett约减来进行优化操作。
Barrett约减算法的整体流程可以概括如下:
step 1.根据p,选定b和k,其中b代表的是基,满足 b ≥ 3 b \ge 3 b≥3, k = ⌊ l o g b p ⌋ + 1 k = \lfloor log_b^p \rfloor+1 k=⌊logbp⌋+1, 0 ≤ z 0 \le z 0≤z < b 2 k \lt b^{2k} <b2k。
step 2.预计算 μ = ⌊ b 2 k / p ⌋ \mu = \lfloor b^{2k} /p \rfloor μ=⌊b2k/p⌋。
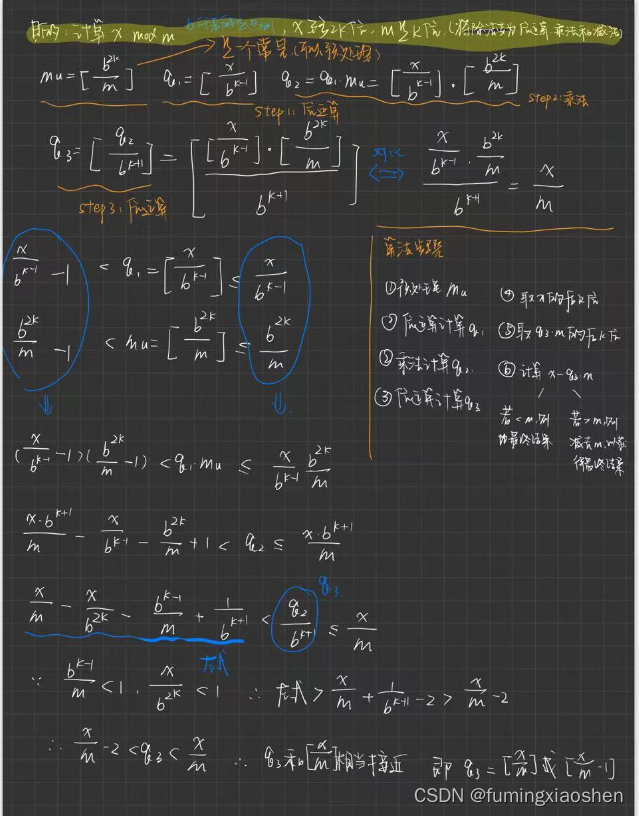
step 3.构造 q ^ \hat{q} q^,使得 q − 2 ≤ q ^ ≤ q q-2 \le \hat{q} \le q q−2≤q^≤q (不等式1)
step 4.优化计算 r = z − q ^ ∗ p r=z-\hat{q}*p r=z−q^∗p
step 5.在两步减法操作内,计算得到最终的r

算法2.14中,使用荧光笔标记了一些运算过程,其中绿色代表移位操作,粉色代表乘法操作,黄色代表加减操作,蓝色代表预处理操作。因此,整个过程,将除法转化为移位、乘法、加减等操作,从而实现了约减去的目的。
此外,对于 r = z − q ^ ∗ p r=z-\hat{q}*p r=z−q^∗p的计算,也存在优化的操作。记 z = z 1 ∗ 2 k + 1 + z 0 z=z_1*2^{k+1}+z_0 z=z1∗2k+1+z0, q ^ ∗ p = u 1 ∗ 2 k + 1 + u 0 \hat{q}*p=u_1*2^{k+1}+u_0 q^∗p=u1∗2k+1+u0。根据推导可以得出 0 ≤ z − q ^ ∗ p < b k + 1 0 \le z-\hat{q}*p \lt b^{k+1} 0≤z−q^∗p<bk+1(不等式2),因此先计算 z 0 − u 0 z_0-u_0 z0−u0(对应算法2.14的第3行),但当存在从 z 1 z_1 z1借位的时候, z 0 − u 0 < 0 z_0-u_0 \lt 0 z0−u0<0,因此此时需要再加上 b k + 1 b^{k+1} bk+1(对应算法2.14的第4行)。
正确性证明
下面主要对于不等式1和不等式2进行数学推导与证明。