一、人寿保险案例(两状态)
人寿保险公司把人的健康状态分为健康和疾病两种,以一年为一个时段,研究健康状态的转变。假设对某一年龄段的人来说,今年健康,明年继续保持健康的概率为0.8,即明年转为疾病的概率为0.2;而今年患病,明年转为健康的概率为0.7,即明年继续保持疾病状态的概率为0.3。
由于投保人处于健康和疾病状态是随机的,故设Xn表示第n年的状态,Xn=1表示健康,Xn=2表示疾病,n=0,1,2,3,….ai(n)表示第n年处于状态i的概率,i=1,2,即an(i)=P{Xn=i},用pij来表示今年处于状态i来年处于状态j的概率,即pij=P(Xn+1=j|Xn=i),i=1,2.绘制成链图,见图(1)。
将上面的描述写成表格,如表1,
表1 两状态的状态转移
称P=(pij)2×2为状态转移概率矩阵。
根据全概率公式,有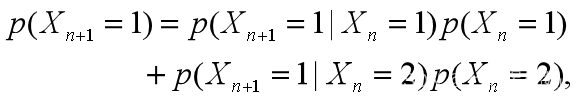

简写为 n=0,1,2,…【1】
n=0,1,2,…【1】
由此可见,投保人第n+1时段的身体健康状态的概率,只与第n时段的状态概率和转移概率有关,与第n-1,n-2,…以前的状态概率无关,这种性质称为无后效性,也称为马尔可夫性质。
记a(n)为第n时段投保人的身体健康状态的概率分布向量,则公式【1】可以简写为矩阵和向量的形式![]() 【2】
【2】
称公式【1】或【2】为状态转移方程,矩阵P称为状态转移矩阵
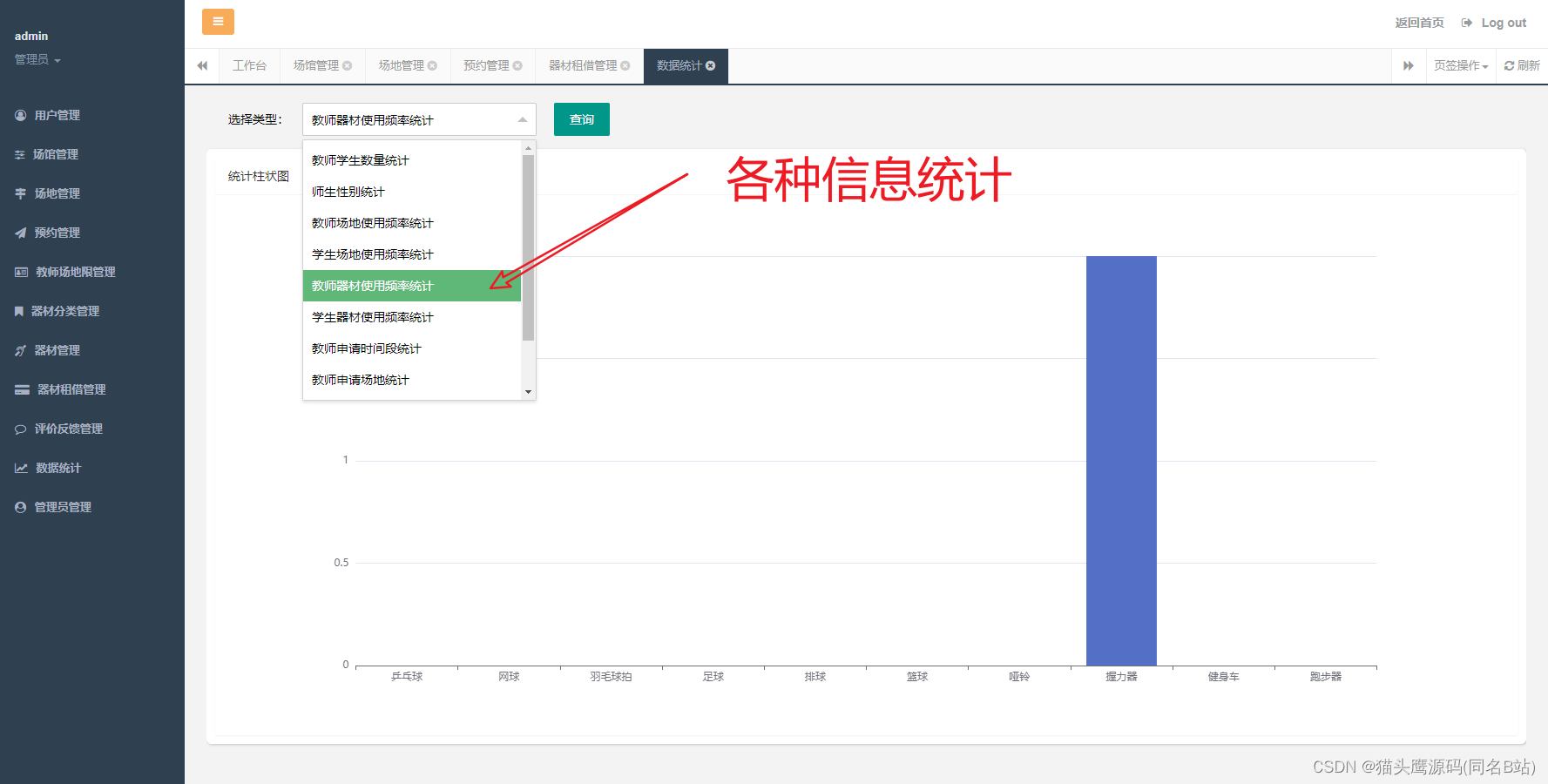
下面假定投保人初始阶段的身体健康状态分布向量,分别取a(0)=[1,0]T,a(0)=[0,1]T,a(0)=[0,75,0.25]T,分别代入公式【2】,计算结果保留在表2中
p=[0.8 0.2;0.7 0.3];
a01=[1,0];a02=[0,1];a03=[0.75,0.25];
A01=[a01;a01*p;a01*p^2;a01*p^3;a01*p^4;a01*p^8];
A02=[a02;a02*p;a02*p^2;a02*p^3;a02*p^4;a02*p^8];
A03=[a03;a01*p;a03*p^2;a03*p^3;a03*p^4;a03*p^8];
A=[A01;A02;A03];
表2 不同初始状态状态转移数据
| n | 0 | 1 | 2 | 3 | 4 | … | ∞ |
| a1(n) | 1 | 0.8 | 0.78 | 0.778 | 0.7778 | … | 0.777778 |
| a2(n) | 0 | 0.2 | 0.22 | 0.222 | 0.2222 | … | 0.222222 |
| a1(n) | 0 | 0.7 | 0.77 | 0.777 | 0.7777 | … | 0.777778 |
| a2(n) | 1 | 0.3 | 0.23 | 0.223 | 0.2223 | … | 0.222222 |
| a1(n) | 0.75 | 0.8 | 0.7775 | 0.77775 | 0.777775 | … | 0.777778 |
| a2(n) | 0.25 | 0.2 | 0.2225 | 0.22225 | 0.222225 | … | 0.222222 |
从表2可以看出
- 无论初始状态的概率分布如何,经过有限次转移后,都会稳定在一个固定的概率分布;
- 从ai(∞)>0,i=1,2可以看出,无论初始状态i如何,总能以概率大于0达到所有状态j;(对于满足(2)的马氏链,称为正则马氏链。)
- 状态转移的每个阶段,转移矩阵P都相同,称为马氏链的时齐性,没有特殊说明,一般研究的马氏链都具有时齐性。
二、人寿保险案例(三状态)
保险公式将人的生存状态定义为三种:健康、疾病和死亡(第三中状态),用Xn=3表示.今年健康,明年可能突发疾病或偶然事件而死亡;今年疾病,明年可能继续疾病、健康或死亡,而一旦死亡,则不能再转为健康或疾病。根据统计,三种状态相互转化的概率如表3.
表3 三状态的状态转移 记ai(n)=P{Xn=i},pij=P{X(n+1)=i|X(n)=j},i,j=1,2,3;n=0,2,…则,此案例中的状态转移方程为
记ai(n)=P{Xn=i},pij=P{X(n+1)=i|X(n)=j},i,j=1,2,3;n=0,2,…则,此案例中的状态转移方程为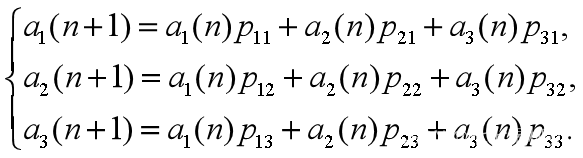 【3】
【3】
将初始状态X01=[1,0,0]T,X02=[0,1,0]T和X03=[0.75,0.25,0]T代入公式【3】,经计算,结果填入表4.
X1=[1,0,0];X2=[0,1,0];X3=[0.75,0.25,0];
p=[0.8 0.18 0.02;0.25 0.65 0.1;0 0 1];
A1=[X1;X1*p;X1*p^2;X1*p^3;X1*p^30;X1*p^60];
A2=[X2;X2*p;X2*p^2;X2*p^3;X2*p^30;X2*p^60];
A3=[X3;X3*p;X3*p^2;X3*p^3;X3*p^30;X3*p^60];
A=[A1,A2,A3]'
表4 不同初始状态的转移结果的数据对比
| 时段n | 0 | 1 | 2 | 3 | 30 | 60 | ∞ |
| a1(n) | 1 | 0.8000 | 0.6850 | 0.6133 | 0.1431 | 0.0307 | 0 |
| a2(n) | 0 | 0.1800 | 0.2610 | 0.2930 | 0.0859 | 0.0184 | 0 |
| a3(n) | 0 | 0.0200 | 0.0540 | 0.0938 | 0.7711 | 0.9509 | 1 |
| a1(n) | 0 | 0.2500 | 0.3625 | 0.4069 | 0.1192 | 0.0256 | 0 |
| a2(n) | 1 | 0.6500 | 0.4675 | 0.3691 | 0.0715 | 0.0154 | 0 |
| a3(n) | 0 | 0.1000 | 0.1700 | 0.2240 | 0.8092 | 0.9590 | 1 |
| a1(n) | 0.75 | 0.6625 | 0.6044 | 0.5617 | 0.1371 | 0.0294 | 0 |
| a2(n) | 0.25 | 0.2975 | 0.3126 | 0.3120 | 0.0823 | 0.0177 | 0 |
| a3(n) | 0 | 0.0400 | 0.0830 | 0.1264 | 0.7806 | 0.9529 | 1 |
从表4可以看出:无论初始状态如何,通过状态转移之后,终究会定格在状态3不改变;若转移概率矩阵中pii=1,称状态i为吸状态,称这样的马氏链为吸收链。
三、马氏链基本概念
1、马氏链及其基本方程
按系统的发展进程,时间离散化为n=0,1,2,…,对每个n,系统的状态为随机变量Xn表示,可以取k个值,Xn=1,2,…,k,记ai(n)=P{Xn=i},即状态概率(分布),从Xn=i到xn+1=j的概率记为pij=P{Xn+1=j|Xn=i},即转移概率。若Xn+1的取值取决于Xn的取值和转移概率,与前面的xn-1,xn-2,…的取值无关,称这种离散状态按照时间转移的过程为马氏链。
称 状态转移概率矩阵,简称转移矩阵,它满足
状态转移概率矩阵,简称转移矩阵,它满足
记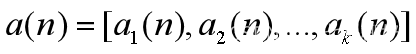 为第n时段的状态概率(分布)行向量。
为第n时段的状态概率(分布)行向量。
称 为马氏链基本方程。
为马氏链基本方程。
在上述公式中,每个两个阶段的状态转移概率矩阵都是同一个矩阵P,称这种性质为马氏链的时齐性。
2、正则链
2.1 正则链定义:从任意状态出发,通过有限次转移,都能到另外的状态。
2.2 马氏链为正则链的充分必要条件←→状态转移矩阵P满足PN>0,即PN的每个分量都大于0.
2.3 正则链存在唯一的极限状态概率w=[w1,w2,…,wk],使得 称w为稳态概率,满足
称w为稳态概率,满足 不难看出,w就是P转置矩阵的征值为1的特征向量的(标准化)行写法。
不难看出,w就是P转置矩阵的征值为1的特征向量的(标准化)行写法。
3、吸收链
若状态转移概率矩阵P中,有pii=1,则称i为吸收态。若马氏链中包含吸收态,则从任何一个非吸收态出发,经过有限次转移,都会以一个正概率到大吸收态。称这样的马氏链为吸收链。
4、首次到大概率和首次平均返回次数
记fij(n)为从状态i出发,经过n次转移,首次到大状态j的首达概率,于是从i到j的平均转移次数为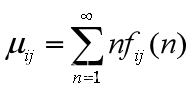 μii称为平均首次返回次数。
μii称为平均首次返回次数。
5、吸收链的转移矩阵
若吸收链有r个吸收态,则转移矩阵P可以写为
 其中方阵Q至少有一个行和小于1.
其中方阵Q至少有一个行和小于1.
且I-Q可逆,满足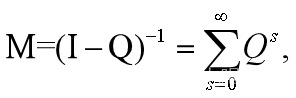 设列向量
设列向量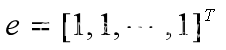
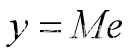 的第i分量表示从第i个非吸收态出发,被某个吸收态吸收的平均转移次数。
的第i分量表示从第i个非吸收态出发,被某个吸收态吸收的平均转移次数。
由于状态一旦进入吸收态,就不会再进入非吸收态,所以,从某个非吸收态i出发,进入某个吸收态j,实际上首达概率fij(n)实际表示从i出发,经过n次转移被j吸收的概率,而 则表示从非吸收态i出发终将被吸收态j吸收的概率。
则表示从非吸收态i出发终将被吸收态j吸收的概率。