课程地址和说明
基础优化方法p2
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
基础优化方法
在讲具体的线性回归实现之前,要先讲一下基础的优化模型的方法
梯度下降
当模型没有显示解(最优解)的时候,用梯度下降法迭代到局部最优值(贪心原则)

- 首先挑选一个随机初始值 w 0 → \overrightarrow{w_{0}} w0;
- 不断更新 w 0 w_{0} w0使得其接近最优解,即 w t → = w t − 1 → − η ∂ ℓ ∂ w t − 1 → \overrightarrow{w_{t}}= \overrightarrow{w_{t-1}}-\eta \frac{\partial \ell}{\partial \overrightarrow{w_{t-1}}} wt=wt−1−η∂wt−1∂ℓ,其中, w t − 1 → \overrightarrow{w_{t-1}} wt−1代表时刻 t t t上一时刻 t − 1 t-1 t−1对应的 w → \overrightarrow{w} w的值, η \eta η是标量,为学习率,是人为设定的(超参数是需要人为指定的值), ∂ ℓ ∂ w t − 1 → \frac{\partial \ell}{\partial \overrightarrow{w_{t-1}}} ∂wt−1∂ℓ代表的是 t − 1 t-1 t−1时刻对应的梯度向量的方向;
- 下图为某多元函数的等高线图:
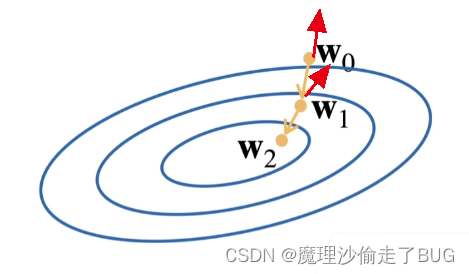
梯度向量的方向是使得函数值增加最快的方向,即与等高线正交的图中的红色向量,而梯度的反方向(即负梯度向量)是使得函数值减少的最快的方向即图中的黄色箭头所指向的方向(所以表达式中要对梯度取负号),也就是按照负梯度方向可以找到函数的极小值,而 η \eta η学习率代表的是沿着负梯度方向一次走多远,比如:随机初始到 w 0 → \overrightarrow {w_{0}} w0这个点(以向量形式表示),则按照学习率乘以负梯度迭代到 w 1 → \overrightarrow {w_{1}} w1
选择学习率
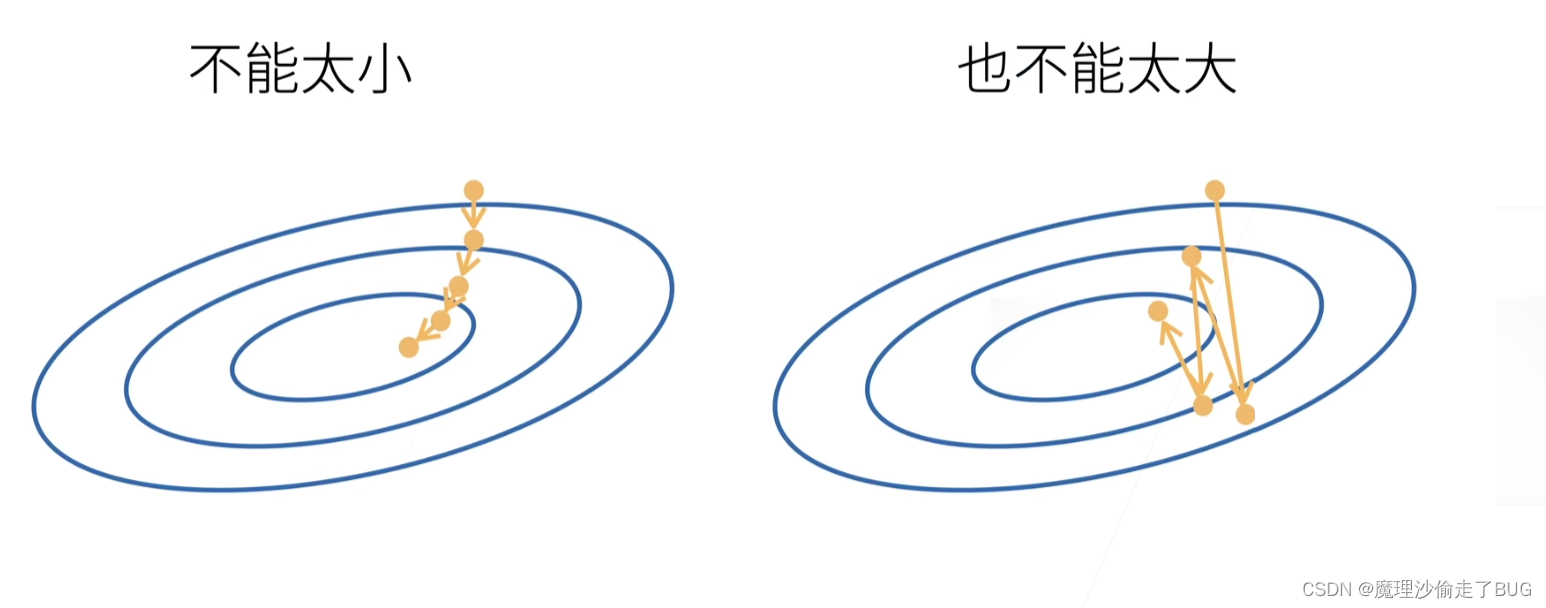
- 如果学习率过小,每一次走的步长有限,走到局部优化点是需要很大代价的;
- 如果学习率过大,会导致迭代振荡,甚至无法走到局部优化点。
小批量随机梯度下降
深度学习方法常采用小批量随机梯度下降

【注】超参数需要人为指定数值。
选择批量大小

总结