满足时间复杂度o(n)的方法:
快排的思想
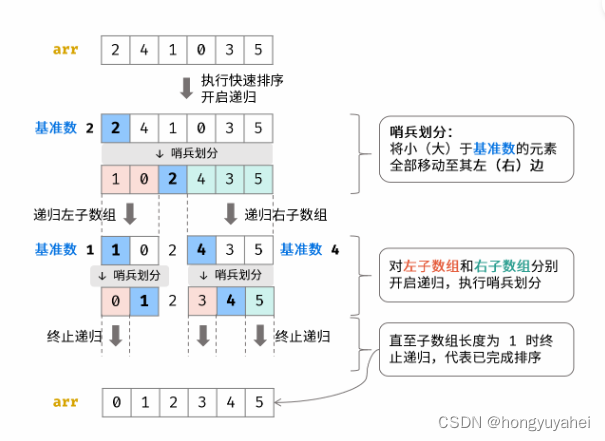

class Solution{
public:int findKthLargest(vector<int>& nums,int k){return quickSelect(nums,k);}
private:int quickSelect(vector<int>& nums,int k){//随机选择基数int privot=nums[rand()%nums.size()];//将大于、小于、等于privot的元素划分至big\small\equal中vector<int> big,equal,small;for(int num:nums){if(num>privot){big.push_back(num);}else if(num<privot){small.push_back(num);}else{equal.push_back(num);}}//第k大元素在big中,递归划分if(k<=big.size()){return quickSelect(big,k);}//第k大元素(第n+1-k小元素)在small中,递归划分if(nums.size()+1-k<=small.size()){//原先第k大,在small中k需减去big和equal集合的大小return quickselect(small,k-(nums.size()-small.size()));}//第k大元素在equal中,直接返回privotreturn privot;}
};