参考文献:
[1]潘虹锦,高红均,杨艳红,等.基于主从博弈的售电商多元零售套餐设计与多级市场购电策略[J].中国电机工程学报,2022,42(13):4785-4800.
1.摘要
随着电力市场改革的发展,如何制定吸引用户选择的多类型零售套餐成为提升售电商利润的研究重点。为此该文结合激励手段和价格信号为售电商设计了多类提升市场竞争力的零售套餐,并基于多时间尺度、多交易类型的市场背景为其提出购电策略。首先,搭建售电商与多元用户之间的主从博弈架构,分析售电商参与日前、月度、年度多级市场下与发电商、电力交易中心等主体之间的多种购电交易类型,设计峰谷分时电价、昼夜用电捆绑、峰谷惩罚补偿、阶梯递增电价、固定单一电价 5 种月度零售套餐。其次,分别以考虑风险因素的售电商效益最大化、多元用户自身综合满意度最大化为目标,构建主方购售电组合决策模型和从方零售套餐选择模型,并阐述主从博弈互动过程。接着,采用粒子群优化算法和 CPLEX 优化软件求解模型的纳什均衡解。最后,利用算例仿真验证主从博弈模型的迭代求解具有较好的收敛性,多级市场购电策略和多元零售套餐的提出有利于售电商提升自身利润的同时提高用户满意度,从而扩大市场份额。
2.原理介绍
2.1 多级市场购电与多元零售套餐设计
售电商在参与电力市场竞争的过程中既要参与多级时间尺度市场进行购电,同时需要设计适应不同类型用户的多元零售套餐,以提升市场份额。在购电侧,本文重点考虑售电商参与日前、月度、年度多级市场,其中月度和年度市场往往签订双边合约,而期权、期货合同等双边交易类型可以有效控制市场风险,因此考虑售电商与发电商签订月度期权合同和年度期货合同。同时售电商还可以与其他售电商签订月度电力转让交易合同,以减轻双方的营业风险。在日前市场,售电商通过集中竞价交易的方式购电,主要用于填补中长期交易以外的电量差额,规避高额偏差考核费用的风险。在售电侧,本文主要设计多元零售套餐以适应具有不同用电特性的电力用户,提升用户满意度。售电商参与购售电交易的过程中,与代表需求侧利益的多个终端用户间存在主从博弈关系,构成一主多从的博弈格局。含售电商参与的主从博弈架构如图 1 所示。

2.2 主从博弈模型
2.2.1 主方(售电商)购售电组合决策模型
(1) 目标函数
售电商通过参与年度、月度和日前多级时间尺度市场组合购电,以及基于价格和激励的需求响应设计多元零售套餐组合售电,提升自身利润,实现自身效益最大化。同时,由于日前市场电价的不确定性,售电商可能面临一定的风险损失,因此本文利用条件风险价值法对售电商进行风险评估,并以考虑风险因素的售电商效益最大化为目标,构建了基于需求响应的售电商购售电组合决策模型,数学表达如下:

(2)约束条件
售电商在参与市场竞争制定购售电策略的过程中需要考虑购售电量平衡约束、期货与转让交易约束、日前市场交易约束、套餐价格约束和风险水平约束。
1)购售电量平衡约束

2)各交易机制的购电量约束。

3)套餐价格约束。

4)风险约束。

2.2.2 从方(用户)零售套餐选择模型
(1) 目标函数
针对于需求侧终端用户,本文以不同套餐下的自身综合用电满意度最大为目标进行套餐选择和用电方式的决策,数学表达如下:
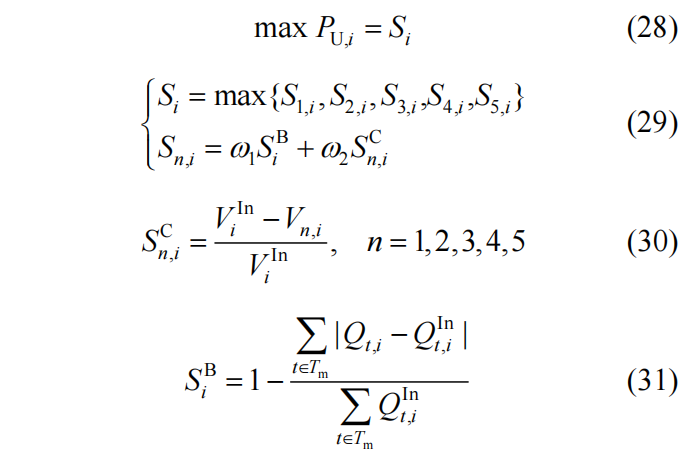

(2) 约束条件
用户在选择零售套餐以提升用电综合满意度的同时,需考虑用电量上下限约束:
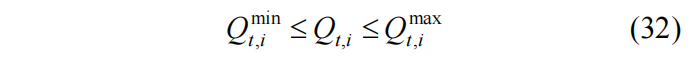
2.2.3 主从博弈数学模型
主从博弈结构可由以下数学模型表达:

含售电商参与的主从博弈互动过程可描述为:售电商结合供给侧各主体制定的多级市场出清电价和用户初始负荷需求曲线,根据考虑风险因素的自身效益最大化原则,确定各级市场的购电量,并制定多元零售套餐的价格参数下发给用户;各用户结合自身用电特性,基于自身综合用电满意度最大化原则,确定所选套餐类型与各时段的用电量上报给售电商;售电商根据各用户上报数据,结合自身利润、风险重新制定各级市场购电量和多元零售套餐价格参数与用户进行二次博弈互动,如此进行迭代求解直到售电商、用户二者均达到自身目标的最值,且任何一方交易主体策略的改变不会导致另一方交易主体改变自身策略时,才能得到博弈互动的最优决策方案,即纳什均衡解。
2.3 主从博弈模型求解方法
粒子群优化算法具有原理简单容易实现、收敛速度较快、需要调整的参数较少等特点,且有一定的记忆性和进化性,能完整保存迭代过程中所有粒子的局部最优解和全局最优解,对分析具体的博弈互动过程有一定的帮助。
粒子群优化算法还可以根据算子更新个体历史最优和群体全局最优,对于本文而言能较好的模拟售电商与用户间博弈互动的过程,同时个体和群体的协同优化有助于快速寻找博弈的均衡解。因此本文考虑采用粒子群优化算法和 Matlab2016a平台下YALMIP工具箱中CPLEX12.6优化软件相结合的方法求解模型的纳什均衡解。对于主方售电商,既采用粒子群优化算法,以售电商利润为纳什适应度函数,求解迭代过程中的最优多元零售套餐参数,又采用CPLEX求解售电商最优多级市场购电策略;对于从方用户,则直接采用CPLEX求解用电策略,保证解的计算效率。模型求解步骤如图 4 所示。

3.编程思路
3.1参数和变量定义

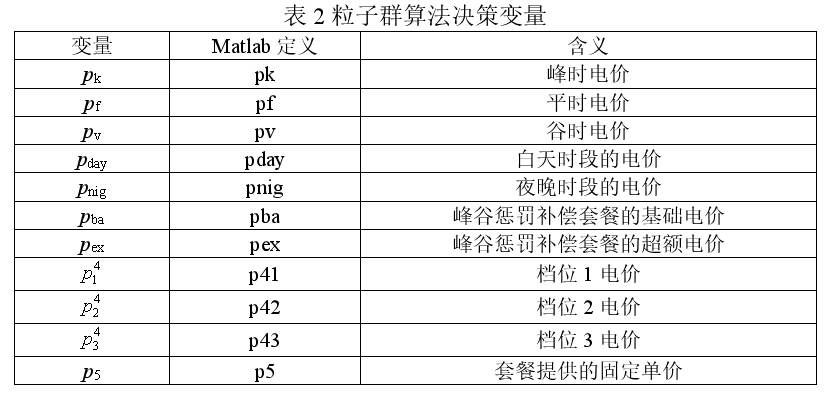


3.2编程思路
根据对文献内容的解读,可以设计下面的编程思路:
步骤1:输入所需数据
这一步比较简单,所需数据文中基本都已给出,按照表1的格式输入matlab中即可,没有给定的参数可以自己假设一个合理的数值。
步骤2:定义上层套餐价格的决策变量
这一步需要按照表2,初始化粒子群算法的决策变量,可以写成下面的形式:

决策变量共有11个,可知粒子群算法的空间维度为11。此外,套餐价格还需满足一定约束条件,主要包括:
- 平时段电价和固定单一电价相等。
- 峰时段电价应高于谷时段电价。
- 白天电价应高于夜间电价。
- 峰谷惩罚补偿套餐的基准电价和固定单一电价相同。
- 阶梯递增电价套餐中第1档电价<第2档电价<第3档电价
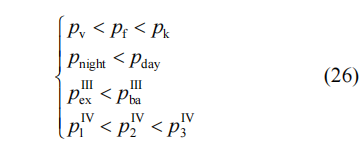
相等的电价,可以通过减少决策变量来实现,其他的约束可以通过修复粒子的位置进行实现。减少后的决策变量如下:

其中决策变量共有9个,粒子群算法的空间维度为9。
步骤3:编写用户套餐优选子程序
用户套餐优选子程序,就是需要根据售电商设定的套餐价格,确定使用户满意度最高的套餐选择方案。原文中提到,用户的决策变量只有Qit。但实际上计算用户用电成本时涉及到一些判断项目,需要引入中间变量,因此实际优化中决策变量的数目更多。
步骤4:编写售电商优化子程序
售电商优化子程序就是通过参与年度、月度和日前多级时间尺度市场组合购电,以及基于价格和激励的需求响应设计多元零售套餐组合售电,提升自身利润,实现自身效益最大化。
步骤5:迭代求主从博弈最优解
通过编写粒子群算法主程序,迭代求主从博弈的最优解。文献中并未解释粒子群算法的适应度函数是如何选取的,代码中使用了归一化的用户满意度和售电商利润作为粒子群算法适应度函数。同时设定了连续5次博弈结果误差不超过0.0001时,认为博弈结束,可以输出结果。
4.matlab代码
文件中共有6个m文件和2个mat文件,功能分别如下:
4.1 main_PSO.m
代码的主程序,运行即可得到优化结果。初始设定种群数为50,最大迭代次数为70,大约需要5小时得到结果。种群数和迭代次数可以调整。
4.2 fitnessfun.m
计算适应度函数。
4.3 main_price.m
使用蒙特卡洛模拟法得到典型电价场景。
4.4 repair_pop.m
对于不满足约束的粒子进行修复。
4.5 sub_retailer.m
售电商优化子程序。
4.6 sub_user.m
用户优化子程序。
5.代码运行结果


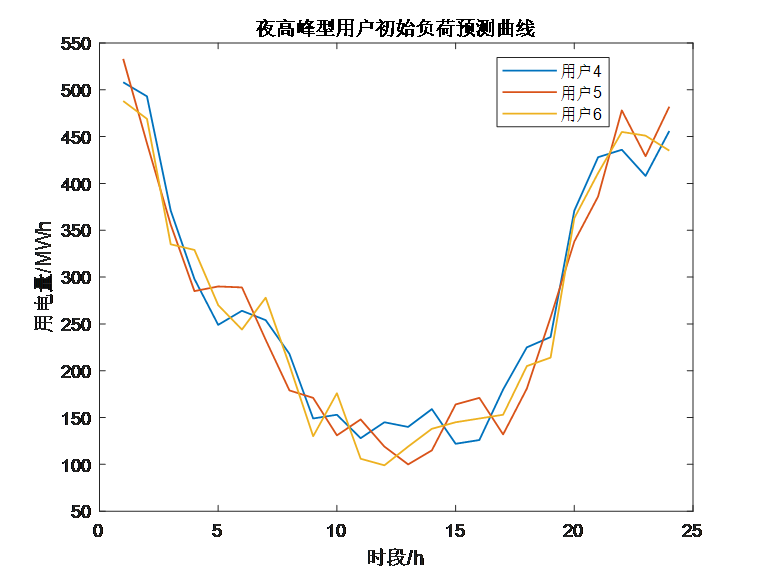




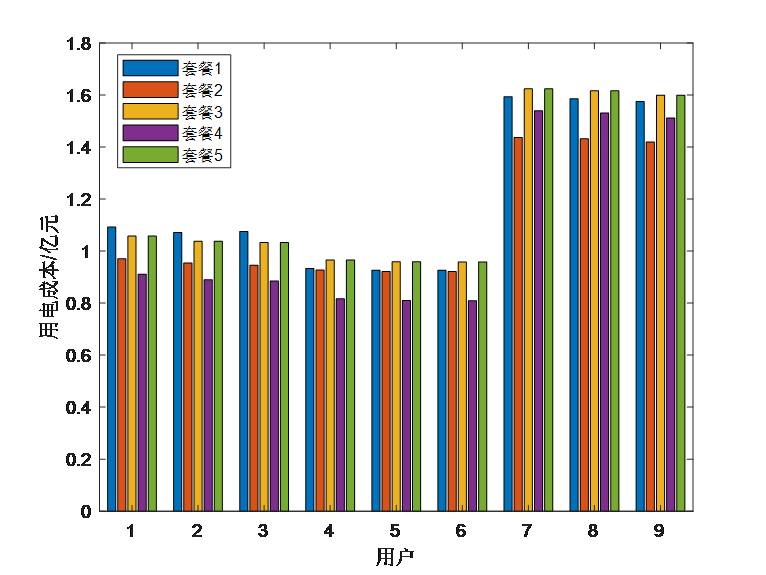
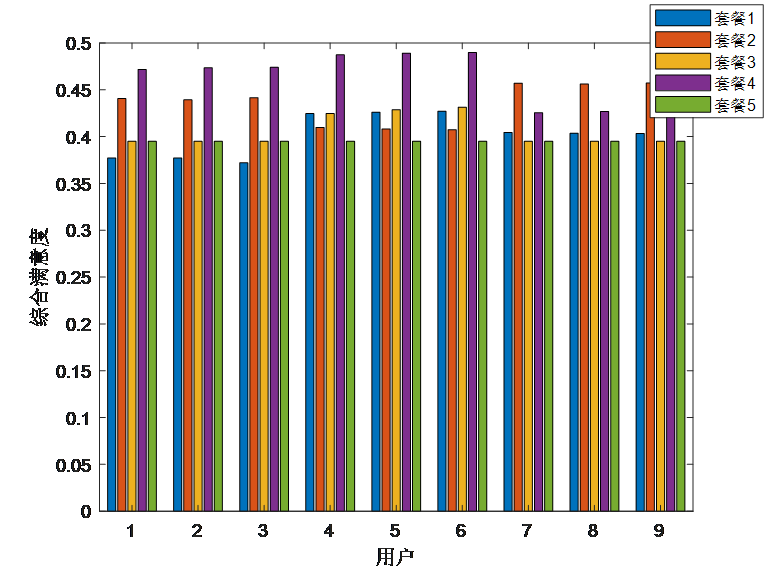

6.代码获取方式
(文章复现)基于主从博弈的售电商多元零售套餐设计与多级市场购电策略matlab代码资源-CSDN文库