LeetCode每日一题：1993. 树上的操作（2023.9.23 C++）

1993. 树上的操作

题目描述：

实现代码与解析：

模拟 + dfs

原理思路：

1993. 树上的操作

题目描述：

给你一棵 n 个节点的树，编号从 0 到 n - 1 ，以父节点数组 parent 的形式给出，其中 parent[i] 是第 i 个节点的父节点。树的根节点为 0 号节点，所以 parent[0] = -1 ，因为它没有父节点。你想要设计一个数据结构实现树里面对节点的加锁，解锁和升级操作。

数据结构需要支持如下函数：

Lock：指定用户给指定节点上锁，上锁后其他用户将无法给同一节点上锁。只有当节点处于未上锁的状态下，才能进行上锁操作。
Unlock：指定用户给指定节点解锁，只有当指定节点当前正被指定用户锁住时，才能执行该解锁操作。
Upgrade：指定用户给指定节点上锁，并且将该节点的所有子孙节点解锁。只有如下 3 个条件全部满足时才能执行升级操作：
- 指定节点当前状态为未上锁。
- 指定节点至少有一个上锁状态的子孙节点（可以是任意用户上锁的）。
- 指定节点没有任何上锁的祖先节点。

请你实现 LockingTree 类：

LockingTree(int[] parent) 用父节点数组初始化数据结构。
lock(int num, int user) 如果 id 为 user 的用户可以给节点 num 上锁，那么返回 true ，否则返回 false 。如果可以执行此操作，节点 num 会被 id 为 user 的用户上锁。
unlock(int num, int user) 如果 id 为 user 的用户可以给节点 num 解锁，那么返回 true ，否则返回 false 。如果可以执行此操作，节点 num 变为 未上锁 状态。
upgrade(int num, int user) 如果 id 为 user 的用户可以给节点 num 升级，那么返回 true ，否则返回 false 。如果可以执行此操作，节点 num 会被升级。

示例 1：

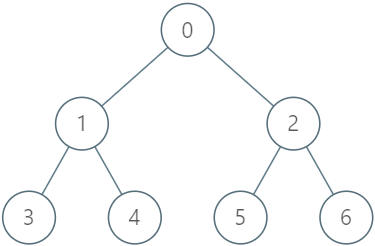
输入：
["LockingTree", "lock", "unlock", "unlock", "lock", "upgrade", "lock"]
[[[-1, 0, 0, 1, 1, 2, 2]], [2, 2], [2, 3], [2, 2], [4, 5], [0, 1], [0, 1]]
输出：
[null, true, false, true, true, true, false]解释：
LockingTree lockingTree = new LockingTree([-1, 0, 0, 1, 1, 2, 2]);
lockingTree.lock(2, 2);    // 返回 true ，因为节点 2 未上锁。// 节点 2 被用户 2 上锁。
lockingTree.unlock(2, 3);  // 返回 false ，因为用户 3 无法解锁被用户 2 上锁的节点。
lockingTree.unlock(2, 2);  // 返回 true ，因为节点 2 之前被用户 2 上锁。// 节点 2 现在变为未上锁状态。
lockingTree.lock(4, 5);    // 返回 true ，因为节点 4 未上锁。// 节点 4 被用户 5 上锁。
lockingTree.upgrade(0, 1); // 返回 true ，因为节点 0 未上锁且至少有一个被上锁的子孙节点（节点 4）。// 节点 0 被用户 1 上锁，节点 4 变为未上锁。
lockingTree.lock(0, 1);    // 返回 false ，因为节点 0 已经被上锁了。

提示：

n == parent.length
2 <= n <= 2000
对于 i != 0 ，满足 0 <= parent[i] <= n - 1
parent[0] == -1
0 <= num <= n - 1
1 <= user <= 104
parent 表示一棵合法的树。
lock ，unlock 和 upgrade 的调用总共不超过 2000 次。

实现代码与解析：

模拟 + dfs

class LockingTree {
public:vector<int> h = vector<int>(2010, -1), e = vector<int>(2010, 0), ne = vector<int>(2010, 0);vector<int> parent; // 方便后面向上遍历int idx = 0; // 邻接表vector<int> flag = vector<int>(2010, 0); // 记录是否上锁void add(int a, int b){e[idx] = b; ne[idx] = h[a]; h[a] = idx++;}LockingTree(vector<int>& parent) {for (int i = 1; i < parent.size(); i++) {add(parent[i], i); // 连接}this->parent = parent;}bool lock(int num, int user) {if (flag[num]) return false; // 已经有人上锁，不能再上flag[num] = user;return true;}bool unlock(int num, int user) {if (flag[num] != user) return false; // 非你上，不能解flag[num] = 0;return true;}bool upgrade(int num, int user) {// 当前节点和其祖先不能有锁for (int i = num; ~i; i = parent[i]) {if (flag[i]) return false;}// 子孙必须有至少一个上锁if (!hasLockedDescendant(num)) return false;// 解锁所有子孙节点unlockDescendants(num);// 上锁当前节点flag[num] = user;return true;}bool hasLockedDescendant(int num) {for (int i = h[num]; i != -1; i = ne[i]) {int child = e[i];if (flag[child] || hasLockedDescendant(child)) {return true;}}return false;}void unlockDescendants(int num) {for (int i = h[num]; i != -1; i = ne[i]) {int child = e[i];if (flag[child]) {flag[child] = 0;}unlockDescendants(child);}}
};