目录
数组如何实现随机访问
两个关键词
数组的特点
根据下标随机访问数组元素
为什么数组要从0开始编号,而不是从1开始
LeetCode之路——704. 二分查找
Code
二分查找算法
数组如何实现随机访问
数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型的数据。
两个关键词
-
第一是线性表(Linear List)。顾名思义,线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组,链表、队列、栈等也是线性表结构。
-
第二个是连续的内存空间和相同类型的数据。正是因为这两个限制,它才有了一个堪称“杀手锏”的特性:“随机访问”。但有利就有弊,这两个限制也让数组的很多 操作变得非常低效,比如要想在数组中删除、插入一个数据,为了保证连续性,就需要做大量的数据搬移工作。
数组的特点
-
相同数据类型:数组中的所有元素必须是相同的数据类型,例如整数、浮点数、字符等。这是因为数组在内存中以相同大小的块存储每个元素,因此元素的数据类型必须一致。
-
固定大小:数组在创建时通常具有固定的大小,这意味着一旦数组的大小确定,就不能轻易改变。如果需要更多或更少的存储空间,通常需要创建一个新的数组。
-
连续存储:数组中的元素在内存中是连续存储的,这使得随机访问非常高效,因为可以通过计算索引位置直接访问元素,而不需要遍历整个数据结构。
-
零基索引:大多数编程语言中,数组的索引从零开始,这意味着第一个元素的索引为0,第二个元素的索引为1,以此类推。
-
随机访问:由于数组中的元素是连续存储的,可以通过索引来快速访问任何元素,这使得数组成为实现随机访问的理想数据结构。
-
固定存储开销:数组的存储开销是固定的,与数组的大小无关。这意味着如果数组的大小为n,那么它的存储开销也为n个元素的大小。
根据下标随机访问数组元素
我们用一个长度为10的int类型的数组int[] a = new int[10]来举例。i数组a[10]的大小为10,计算机给分配了一块连续的内存空间1000-1039,这块内存的首地址是base_address=1000.
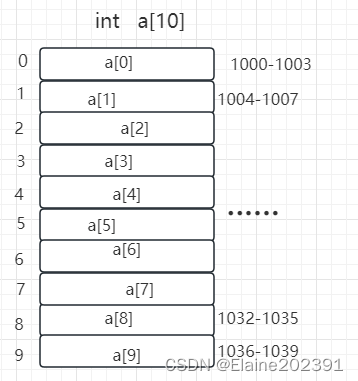
计算机访问内存中的数据时通过内存单元分配的地址,寻址公式:
a[i]_address = base_address + i * data_type_size
其中data_type_size表示数组中每个元素的大小。我们举的这个例子里,数组中存储的是int类型数据,所以data_type_size就为4个字节。
为什么数组要从0开始编号,而不是从1开始
从数组存储的内存模型上来看,“下标”最确切的定义应该是“偏移(offset)”。前面也讲到,如果用a来表示数组的首地址,a[0]就是偏移为0的位置,也就是首地 址,a[k]就表示偏移k个type_size的位置,所以计算a[k]的内存地址只需要用这个公式:
a[k]_address = base_address + k * type_size
但是,如果数组从1开始计数,那我们计算数组元素a[k]的内存地址就会变为:
a[k]_address = base_address + (k-1)*type_size
对比两个公式,我们不难发现,从1开始编号,每次随机访问数组元素都多了一次减法运算,对于CPU来说,就是多了一次减法指令。 数组作为非常基础的数据结构,通过下标随机访问数组元素又是其非常基础的编程操作,效率的优化就要尽可能做到极致。所以为了减少一次减法操作,数组选 择了从0开始编号,而不是从1开始。
LeetCode之路——704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2 输出: -1 解释: 2 不存在 nums 中因此返回 -1
提示:
-
你可以假设 nums 中的所有元素是不重复的。
-
n 将在 [1, 10000]之间。
-
nums 的每个元素都将在 [-9999, 9999]之间。
分析:
-
有序数组、数组中无重复元素 ——> 二分查找算法
-
特殊场景:
-
n=1
-
target<nums[0]或者target>nums[n-1]
-
Code
class Solution {public int search(int[] nums, int target) {// 有序数组,元素不重复 ——> 二分查找算法int result = -1;// 特殊场景:target < nums[0] 或者 target > nums[n-1]int left = 0;int right = nums.length - 1;if (target < nums[left] || target > nums[right]) {return result;}while (left <= right) {int middle = left + ((right - left) >> 1);if (target < nums[middle]) {right = middle - 1;} else if (target > nums[middle]){left = middle + 1;} else {return middle;}}return result;}
}
二分查找算法
二分查找算法(Binary Search)是一种用于在有序数组中查找特定元素的高效搜索算法。它的工作原理是将数组分成两半,并比较中间元素与目标元素的大小关系,然后根据比较的结果决定继续在左半部分或右半部分继续查找,以此类推,直到找到目标元素或确定目标元素不存在为止。
以下是二分查找的基本步骤:
-
确定搜索范围的起始点(通常为数组的第一个元素)和结束点(通常为数组的最后一个元素)。
-
计算中间元素的索引:
(起始点 + 结束点) / 2。如果是整数除法,向下取整。 -
比较中间元素与目标元素的值:
-
如果中间元素等于目标元素,查找成功,返回中间元素的索引。
-
如果中间元素大于目标元素,说明目标元素可能在左半部分,将结束点更新为中间元素的前一个位置。
-
如果中间元素小于目标元素,说明目标元素可能在右半部分,将起始点更新为中间元素的后一个位置。
-
-
重复步骤2和步骤3,直到找到目标元素或搜索范围为空(起始点大于结束点),此时目标元素不存在于数组中。
二分查找是一种高效的算法,其时间复杂度为 O(log n),其中 n 是数组的大小。
参考资料:程序员Carl 代码随想录