快速排序的概念

快速排序是通过二叉树的思想，先设定一个值，通过比较，比它大的放在它的右边，比它小的放在它的左边；这样相当于在二叉树中，小的放在左子树，大的放在右子树，设定的值就是根；再通过递归的思想，将它们继续按这种方式进行排序，排到最后就排好了；这就是快速排序的概念。

void QuickSort(int* a, int left,int right)
{//终止条件if (left >= right){return;}//获取key值，为递归条件做准备int key = PartSort(a, left, right);//key变为分隔的中间值了QuickSort(a, left, key - 1);QuickSort(a, key + 1, right);}

在现在常见的递归函数中，有几个版本（改变PartSort）；

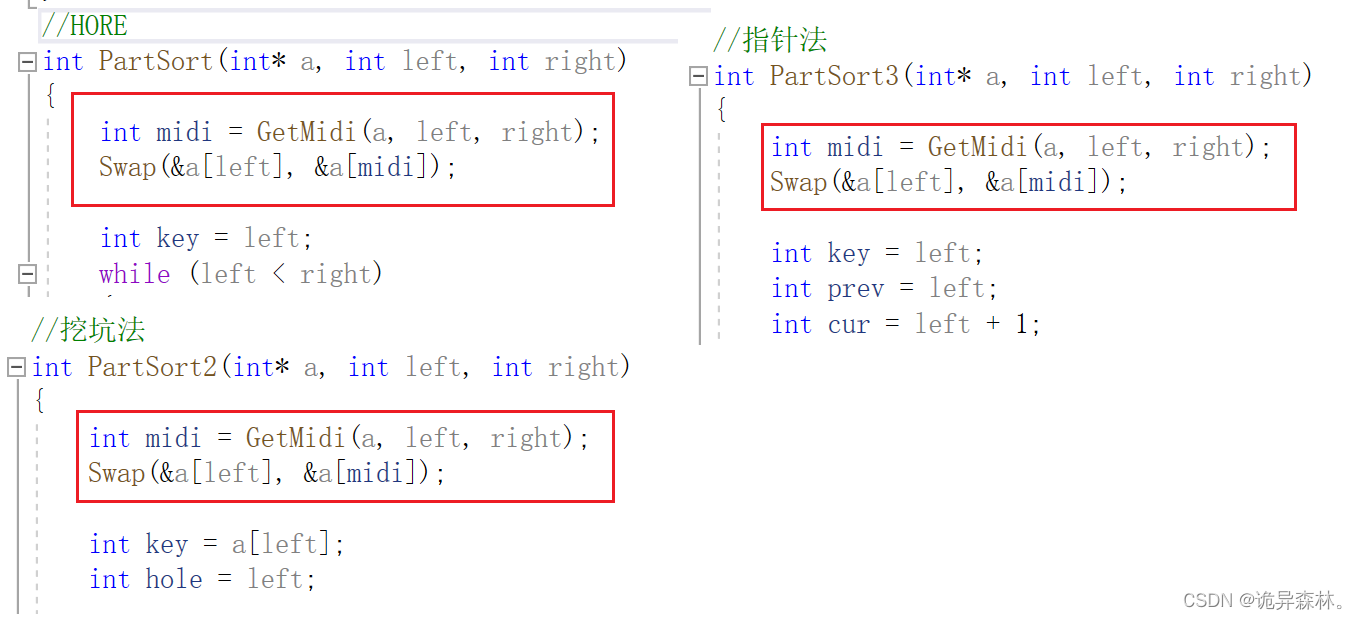
Hoare版本

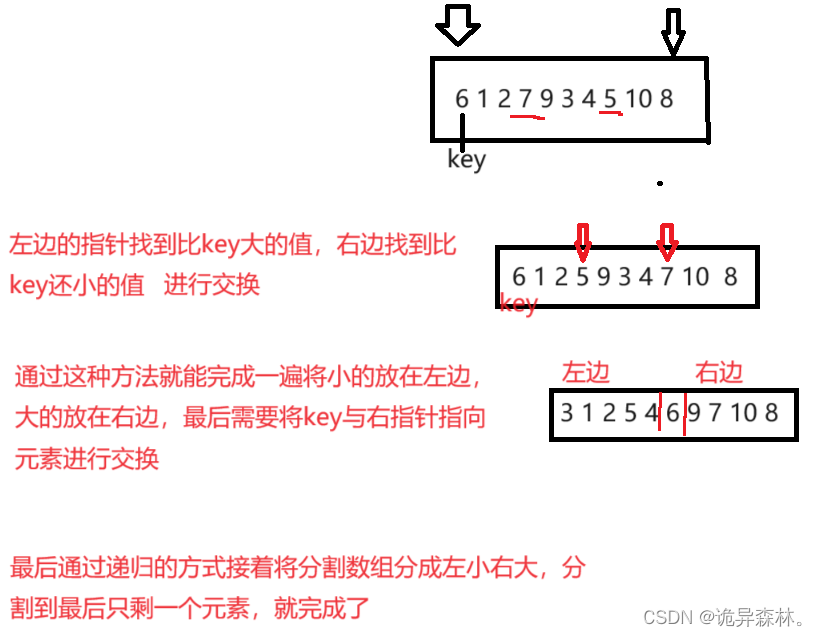
//HOARE
int PartSort(int* a, int left, int right)
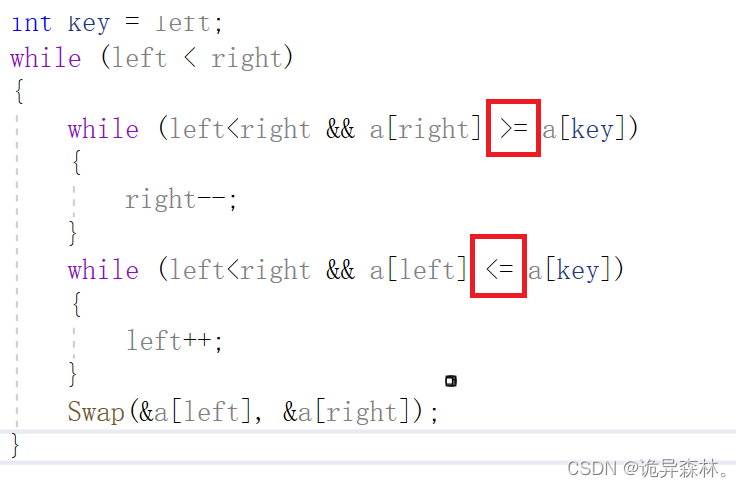
{int key = left;while (left < right){while (left<right && a[right] >= a[key]){right--;}while (left<right && a[left] <= a[key]){left++;}Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);return left;
}

函数进来我们总会以最左边的left变为key，由于最后需要实现位置交换，不能将key记住值，而应该是下标，这样才能进行位置交换，否则只是一个复制的值而已，无法实现位置交换。

内层循环为什么也要写left<right？
对于循环来说，不像if语句一样，只判断一次，while语句会不断的进行判断，然后执行里面的语句；如果对于条件符合的话，那么left就有可能超过了left，left位置不定，可能会越界或者造成数据混乱，所以也要在内层循环中加上这个条件。

当左右指针指定的值与key判断时，至少需要一个指针指向的元素需要判断等于key指向的元素，

如果没有加上的话，举个例子：
6 1 2 6 4 5 7 8 9 6 10，左右指针会指向6，进行交换后还是6，将会陷入死循环；

我们在最后a[key]和a[left]进行交换的时候，没有进行交换判断，是怎么确保a[left]小于key的呢？
在内层循环中，我们是先走的是右指针，再走左指针；这样就保证了right只有走到小于a[key]或者遇到left才会停下。
left初始位置至少也是a[key]怎么说都会小于等于a[key];
这样就保证在终止条件下，a[left]总会小于等于a[eky]；

挖坑法

有人觉得上面的方法需要通过先右指针先走，再左指针走太麻烦了，所以有了个挖坑法；

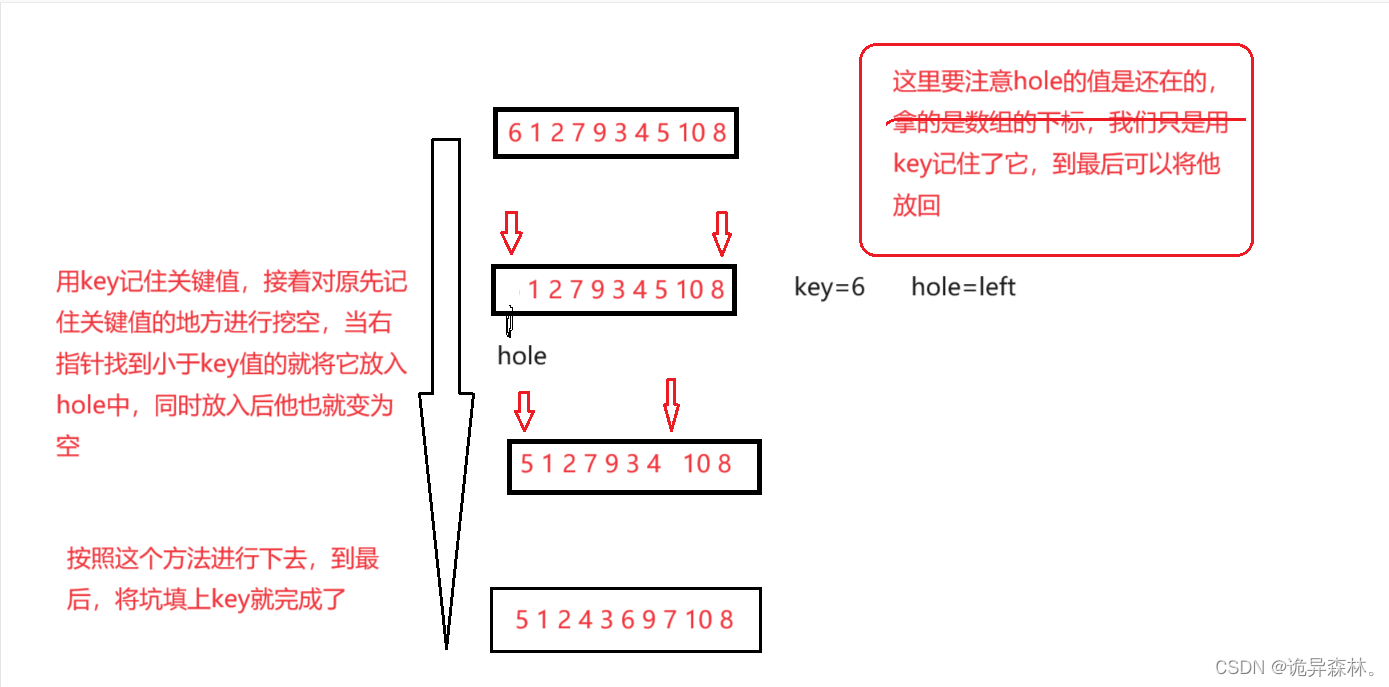
//挖坑法
int PartSort2(int* a, int left, int right)
{int key = a[left];int hole = left;while (left < right){while (left < right && a[right] >= key){right--;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;return left;
}

前后指针法

通过定义两个指针，通过一定要求，将小的值一直往数组前面丢；

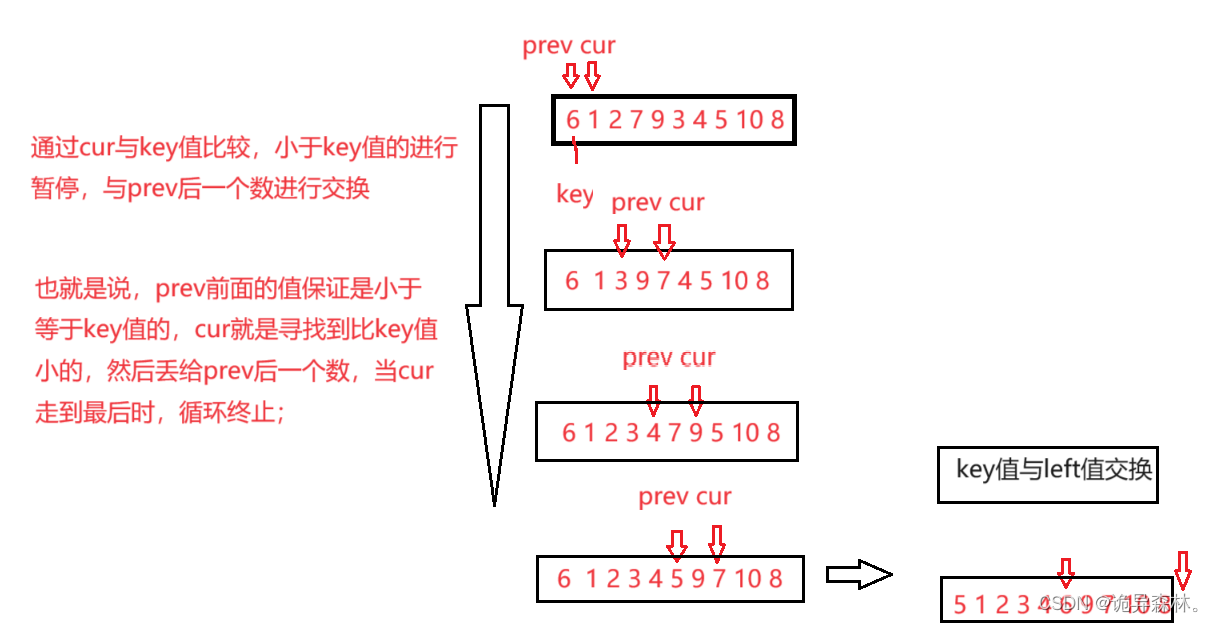
//指针法
int PartSort3(int* a, int left, int right)
{int key = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[key] && ++prev!=cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[key], &a[prev]);return prev;
}

cur指针是用来循环遍历的，可以一直cur++；而只有满足if语句条件时，才进行交换；

验证：

void TestQuickSort1()
{int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 };QuickSort(a, 0,sizeof(a) / sizeof(a[0])-1);PrintfArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{TestQuickSort1();return 0;
}

快速排序的优化

一般来说，快速排序的时间复杂度为O(N*logN)

三数取中法

我们对于key的取值，都是取最左边的数（left），如果一开始数组就是有序的话，我们的快速排序就是O(N^2);

所以就有了三数取中法这种优化方法：通过left、mid中间值、right这三个位置的值进行比较、取它们三个数排中间大的数；这样就会可避免上面这种极端情况；

int GetMidi(int* a, int left, int right)
{int midi = (left + right) / 2;if (a[midi] > a[left]){if (a[midi] < a[right]){return midi;}//上面条件不成立，也就默认a[mid]是最大的了else if (a[right] > a[left])//midi最大{return right;}else{return left;}}else{if (a[midi] > a[right]){return midi;}//上面条件不成立，也就默认a[mid]是最小的了else if (a[left] > a[right]) //midi最小{return right;}else{return left;}}
}

先判断中间数和左数的大小，再判断中间数和右数的大小

小区间用插入排序

对于小区间来说，如果使用递归的方式来实现排序，会使用比较多的时间

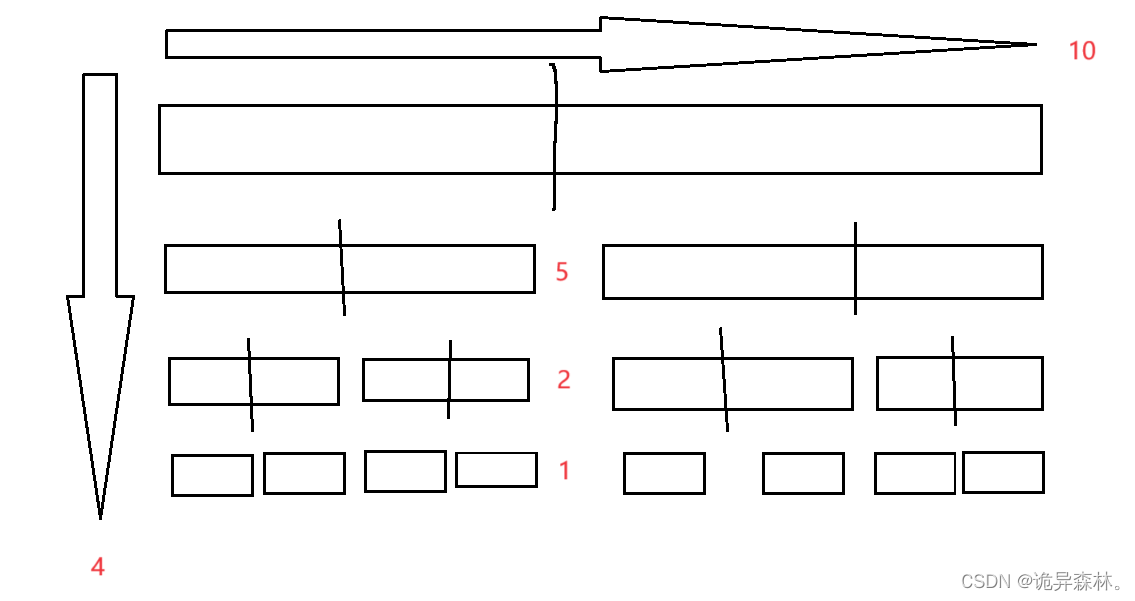
如果使用插入排序，当区间小于10时，对于有预排序的数组来说，插入排序会快很多，而快速排序通过不断的递归，就相当于实现预排序；我们可以验证一下。

void QuickSort(int* a, int left,int right)
{//终止条件if (left >= right){return;}//对于递归的分割，当分割区间小于10，用直接插入排序if ((right - left + 1) > 10){int key = PartSort3(a, left, right);//key变为分隔的中间值了QuickSort(a, left, key - 1);QuickSort(a, key + 1, right);}else{InsertSort(a + left, right - left + 1);}
}void TestQuickSort1()
{isrand(time(NULL));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);//赋值for (int i = 0; i < N; i++){a1[i] = rand();}int begin5 = clock();QuickSort(a1, 0,N-1);int end5 = clock();printf("QuickSort:%d\n", end5 - begin5);
}

非递归的快速排序

我们可以利用栈来模拟实现快速排序的递归方式，但这与用递归实现的排序在本质是不同的，递归需要不断的开辟栈区的空间，而我们将使用动态栈，占用的是堆区的空间，堆区的空间比栈区的大得多，在一定程度上能避免空间溢出；

使用数据结构的栈，利用它的后进先出的道理，可以实现递归的效果；

//利用入栈的方法思想递归方式
void QuickSortNonR(int* a, int left, int right)
{//创栈ST stack;STInit(&stack);//先将第一个插入STPush(&stack, right);STPush(&stack, left);while (!STEmpty(&stack)){int key = PartSort2(a, left, right);if (key + 1 < right){STPush(&stack, right);STPush(&stack, key + 1);}if (left < key - 1){STPush(&stack, key - 1);STPush(&stack, left);}//更新左右指针left = STTop(&stack);STPop(&stack);right = STTop(&stack);STPop(&stack);}STDestory(&stack);
}

在循环里面，还需要判断左右指针的位置，因为需要判断最后进入栈的序列下标，循环还需要完成排序取出下标的数组；

验证：

void TestQuickSort2()
{int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 };QuickSortNonR(a, 0, sizeof(a) / sizeof(a[0]) - 1);PrintfArray(a, sizeof(a) / sizeof(a[0]));
}