题目：

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

来源：力扣（LeetCode）
链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

示例：

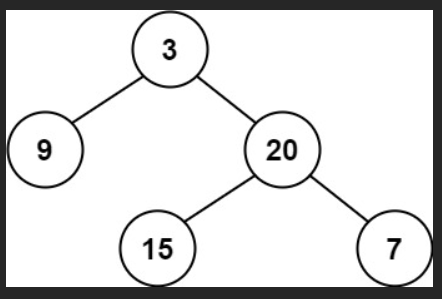
示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

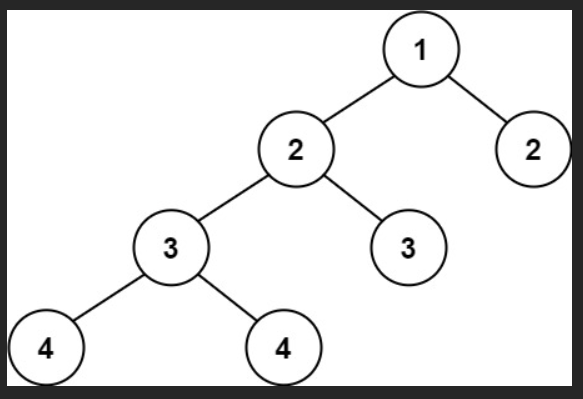
示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

解法：

使用后序遍历，先处理左子树，接着处理右子树，然后处理根结点。

如果当前结点没有左子树和右子树，记录[0, 0]，存在result中。

如果当前结点只有左子树，记录[max(result[-1]) + 1, 0]，替换result最后1个元素，替换的目的是保证result中最后2个元素中有至少1个是当前结点的子树。如果max(result[-1]) + 1已经大于1，说明此时左子树的深度大于等于2，而右子树的深度为0，所以返回False。

如果当前结点只有右子树，同理只有左子树的情况。

如果当前结点有左子树和右子树，记录[max(result[-2]) + 1, max(result[-1]) + 1]，删除result中最后2个元素并添加新记录，这样操作的目的同样是保证result中最后2个元素中有至少1个是当前结点的子树。如果max(result[-2]) + 1和max(result[-1]) + 1相差大于1，说明此时已不满足平衡的条件，返回False。

最后返回True，因为不平衡的情况会中途返回False，所以，如果没有中途返回说明是平衡二叉树。

知识点：

1.平衡二叉树：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

代码：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def isBalanced(self, root: Optional[TreeNode]) -> bool:result = []stack = []while root or stack:while root:stack.append(root)root = root.left if root.left else root.rightroot = stack.pop()if root.left is None and root.right is None:result.append([0, 0])elif root.left and root.right is None:if (t1 := max(result[-1]) + 1) > 1:return Falseresult[-1] = [t1, 0]elif root.left is None and root.right:if (t2 := max(result[-1]) + 1) > 1:return Falseresult[-1] = [0, t2]else:if abs((t3 := max(result[-2]) + 1) - (t4 := max(result[-1]) + 1)) > 1:return Falseresult.pop()result[-1] = [t3, t4]root = stack[-1].right if stack and stack[-1].left == root else Nonereturn True