课程地址和说明

线性回归的从零开始实现p3
本系列文章是我学习李沐老师深度学习系列课程的学习笔记，可能会对李沐老师上课没讲到的进行补充。

线性回归的从零开始实现

不使用任何深度学习框架提供的计算功能，只使用PyTorch提供的Tensor来实现线性回归
我们将从零开始实现整个方法，包括数据流水线、模型、损失函数和小批量随机梯度下降优化器。
首先我们要安装李沐老师提供的一个d2l包，安装方法见视频评论区，导入必要的库

%matplotlib inline
import random
import torch
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE" # jupyter notebook运行d2l内核挂掉解决方法
from d2l import torch as d2l

• 

# 生成训练集
def synthetic_data(w, b, num_example):# 生成y= Xw+b+噪声X = torch.normal(0, 1, (num_example, len(w)),dtype=torch.float32) # 生成均值为0方差为1的随机数，行数是n个样本数，列数是len(w)print(X)y = torch.matmul(X, w)+b # y=Xw+by += torch.normal(0, 0.01, y.shape) # 生成均值为0，方差为1的随机噪音，形状与y相同return X, y.reshape((-1,1)) # 把X和y做成一个列向量返回,-1是说不指定行数，1是指定为一列，即列向量true_w = torch.tensor([2,-3,4],dtype=torch.float32)
true_b = 4.2
# 生成特征和标签（即训练集）
features, labels = synthetic_data(true_w, true_b, 1000) # 样本数为1000
# 打印训练样本
print("特征[0]：",features[0],"\n标签[0]：",labels[0])

运行结果：
特征[0]： tensor([ 1.3343, -1.3974, -1.3717])
标签[0]： tensor([5.5832])

• 画一下生成的训练集

# 画一下生成的训练集
d2l.set_figsize()
# 将第二个特征（下标为1）和最终的真实值（标签）画在二维图像中
d2l.plt.scatter(features[:,1].detach().numpy(), # 将特征的tensor从计算图中detach出来才能转到numpy对象labels.detach().numpy(),1);

运行结果：

• 定义一个data_iter函数，该函数接受批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量

# 数据迭代器
# 这个函数的作用是先打乱样本数据的下标，然后每隔1个batch_size取一次下标
# 并将当前样本的下标以及其后面的batch_size-1个样本的下标存入一个张量之中
# 返回这个存储下标的张量中的各下标对应的特征值和标签
def data_iter(batch_size, features, labels):num_examples = len(features) #样本数量即是特征矩阵的行数，特征矩阵的每一列对应着不同的特征indices = list(range(num_examples)) # 生成每一个样本对应的下标（从0开始）# 将样本的下标打乱，以做到让这些样本是随机读取的，没有特定的顺序# 这样就能以随机的顺序访问每一个样本random.shuffle(indices)# 从0开始到样本数量（左闭右开），每一次隔batch_size大小访问for i in range(0, num_examples, batch_size):# batch_indices每隔batch_size取一次下表存入张量中# 使用min(i+batch_size,num_examples)是因为有可能下标会超出范围# 所以要取每隔batch_size后的下标与张量向量的最大下标中最小的一个作为左闭右开区间的右侧值batch_indices = torch.tensor(indices[i:min(i+batch_size,num_examples)])yield features[batch_indices], labels[batch_indices] # yield返回单个返回值并记住返回的位置，下一次迭代从这个位置开始（方便迭代）# 假定batch_size 为10 
batch_size = 10for X,y in data_iter(batch_size, features, labels):print(X,'\n',y)break # 加个break先迭代一次看看，应该会显示10个样本的特征和其对应的标签

运行结果：
tensor([[-0.1669, 0.6399, 1.8548],
[-0.9414, -1.1511, -0.2822],
[ 0.3021, -0.5745, -0.8592],
[-0.0539, -0.8632, -1.8610],
[ 1.4092, 2.3873, -1.7796],
[-0.0033, -0.2928, -1.1324],
[ 0.4779, 1.7110, -0.0561],
[-0.3564, -0.5307, -0.2051],
[ 0.9909, -0.0604, -0.2683],
[ 1.6115, 0.9627, 0.8231]])
tensor([[ 9.3663],
[ 4.6398],
[ 3.0753],
[-0.7490],
[-7.2540],
[ 0.5359],
[-0.1931],
[ 4.2597],
[ 5.2664],
[ 7.8300]])

• 做完上述步骤，数据就搞定了，接下来定义初始化模型参数

# 定义初始化模型参数
# 需要计算梯度requires_grad=True
w = torch.normal(0, 0.01, size=(3,1), requires_grad=True) # w初始化为一个均值为0，方差为0.01的列数为3（3个特征，视频里那个两个特征有问题）的正态分布的向量
# 偏差直接置为0，标量，所以第一个参数是1
b = torch.zeros(1, requires_grad=True)

• 定义模型 ，损失函数

# 定义模型
def linreg(X, w, b):return torch.matmul(X,w)+b
# 定义损失函数
def squared_loss(y_hat, y):# 返回均方损失return (y_hat - y.reshape(y_hat.shape))**2/2

• 定义优化算法

# 定义优化算法
# 小批量随机梯度下降
# lr是学习率, param是前一个点的向量（随机初始化）
def sgd(params, lr, batch_size):# with语法的好处在于，它确保资源的正确释放，即使在发生异常的情况下也能够被处理# 更新的时候不要有梯度的计算with torch.no_grad():for param in params:# 按批量梯度下降公式写（要求均值）param -= lr * param.grad / batch_size# 不要累积梯度，将梯度设置为0param.grad.zero_()

• 训练过程

# 训练过程
# 指定超参数
lr = 0.03 # 学习率
num_epochs = 3 # num_epochs指的是把整个数据扫描几遍（目前设置为3）
net = linreg # 网络：线性回归
loss = squared_loss # 损失函数：均方损失# 每次扫epoch次数据
for epoch in range(num_epochs):# 遍历数据for X, y in data_iter(batch_size, features, labels):# 预测值是net(X,w,b)，对应的是线性回归，真实值是y，l是求得其损失l = loss(net(X,w,b),y) # 对均方损失的向量求和，求和后计算梯度（对应均方损失函数的公式）l.sum().backward()# 得到梯度后，使用小批量随机梯度下降法对梯度进行更新，传入[w,b]参数sgd([w,b], lr, batch_size)# 用优化好的参数，对所有的样本求损失，看作验证集，故不需要梯度来更新参数with torch.no_grad():train_l = loss(net(features, w, b), labels)print(f'epoch{epoch + 1}, loss{float(train_l.mean()):f}')

运行结果：
epoch1, loss0.045511
epoch2, loss0.000137
epoch3, loss0.000050
可以看到，迭代次数多了，损失函数越小

• 比较真实参数和通过训练学到的参数来评估训练的成功程度

print ( f'w的估计误差（真实值与预测值误差）:{true_w-w.reshape(true_w.shape)} ' )
print ( f'b的估计误差（真实值与预测值误差）:{true_b-b}')

运行结果：

w的估计误差（真实值与预测值误差）:tensor([-0.0003, -0.0005, 0.0003], grad_fn=<SubBackward0>)
b的估计误差（真实值与预测值误差）:tensor([0.0004], grad_fn=<RsubBackward1>)
这个误差很小了

• 注意
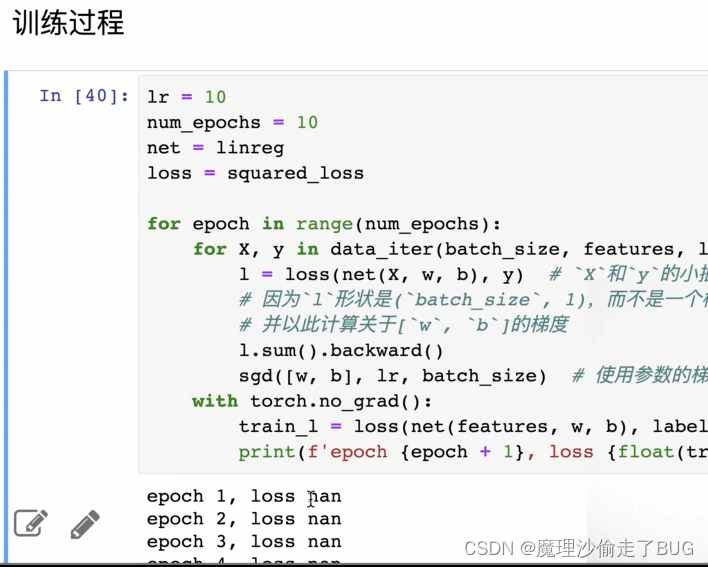
  学习率不能太大太小，如果学习率特别小，跑很多次才能将损失减小，学习率太大会震荡，会出现无穷大的值
  学习率太小的情况：
  
  学习率太大的情况：

• 直接打印w和b就得到了你预测模型的参数，然后对比一下真实值就知道你和真实的线性回归相差多少了。