文章目录
- 写在前面
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:两个哈希表
- 方法二:滑动窗口
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【滑动窗口】【字符串】
题目来源
面试经典 150 | 30. 串联所有单词的子串

题目解读
找出字符串数组 words 中字符串按任意顺序组成的新字符串在字符串 s 中的开始索引,以数组的形式返回。其中,words 中所有字符串的长度都相同。
解题思路
首先,我们记 sLen 为字符串 s 的长度,wsLen 为字符串数组 words 的长度,wLen 为字符串数组中每个字符串的长度。
本题的解题思路其实一目了然:判断 s 中长度为 wsLen * wLen 的子串是否可以由 words 中字符串按任意顺序组合而成(下文以匹配代之),如果可以的话,那么长度为 wsLen * wLen 的 s 子串的开始索引就是有效的答案,加入答案数组 res 即可。
本题关键就是如何判断是否 “匹配”。
方法一:两个哈希表
我们使用两个哈希表来辅助 “匹配”。
第一个哈希表 mp1 用来记录 words 中的字符串出现的次数,第二个哈希表 mp2 用来记录当前长度为 wsLen * wLen 的子串中长度为 wLen 的字符串出现次数,第二个哈希表更新结果如下图所示,其中字符串 s = barfooche,wsLen = 1,wLen = 3:

如果 mp2 中有任何一个字符串出现的次数大于在 mp1 中出现的次数,或者mp2 中有一个字符串没有在 mp1 中出现过,则匹配失败。
具体实现中,我们可以边更新 mp2,边匹配:
- 迭代长度为
wsLen * wLen的s子串中的所有字符串进行,记当前的字符串为ss; - 首先判断
ss是否在mp1中,如果不在,当前长度为wsLen * wLen的s子串一定不匹配; - 如果在,则更新
mp2,接着判断mp2[ss]与mp1[ss]的大小关系,如果前者大,则当前长度为wsLen * wLen的s子串一定不匹配。 - 如果迭代完长度为
wsLen * wLen的s子串中的所有字符串都没有出现以上不匹配的情况,则说明长度为wsLen * wLen的s子串的开始索引就是有效的答案,加入答案数组res即可。
但是,实际测试,方法一超时。我觉得问题在于【先枚举滑窗再枚举单词数】,如果像答案那样【先枚举单词数,再跳跃枚举滑窗】
还有【一次哈希】的解法,不论是一次哈希还是两次哈希最坏的时间复杂度都达到 了 1 0 8 10^8 108,是这样计算的 1 0 4 × 1 0 3 × 30 = 1 0 8 10^4 \times 10^3 \times 30 = 10^8 104×103×30=108,官方题解的时间复杂度为 1 0 3 × 1 0 4 ÷ 30 × 30 = 1 0 7 10^3 \times 10^4 \div 30 \times 30 = 10^7 103×104÷30×30=107,就差那一点最后两个测试用例就没通过。
该方法超时了,实现代码 就不贴出来了。
方法二:滑动窗口
此时利用的是 438. 找到字符串中所有字母异位词 方法二中的优化版的滑动窗口来解决,可以参考 滑窗 differ 优化 进行理解。
其实方法一也是利用的滑动窗口,其中的长度为 wsLen * wLen 的 s 子串就是一个固定的窗口下的子串,不同于方法一【先枚举所有的滑窗再枚举单词数】,方法二的滑窗是【先枚举单词数,再跳跃枚举滑窗】,现在来具体看一看是如何实现的。
首先需要将 s 划分为单词组,每个单词的大小均为 wLen,一共有 wLen 中划分方式。如下图所示为 s = "barfooche",words = ["bar", "foo"] 对于 s 的三种划分方式。
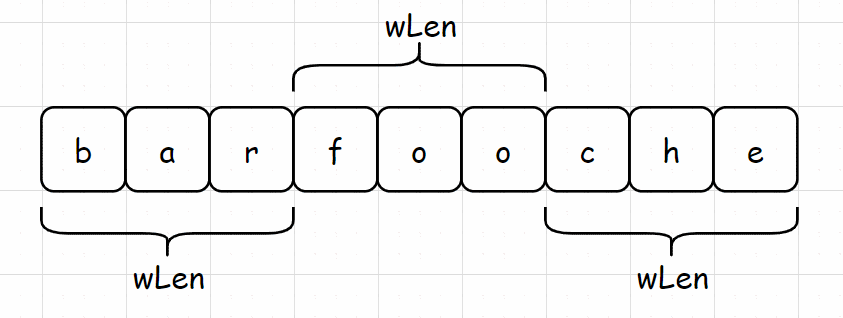
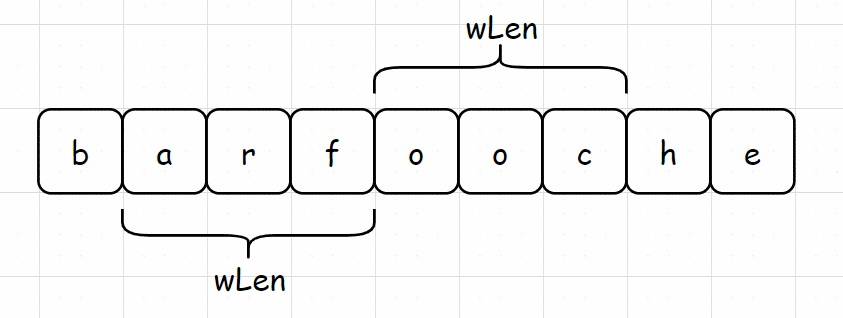
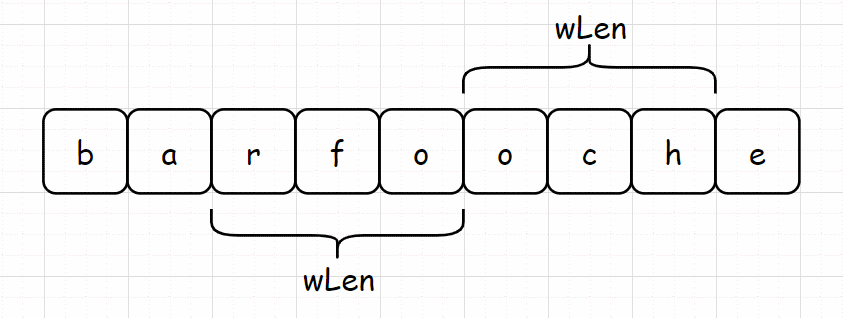
划分成单词组后,一个滑窗包含 s 中前 wsLen 个单词,用一个哈希表 differ 来表示窗口内单词频次和 words 中单词频次之差。初始化 differ 时,出现在窗口中的单词,每出现一次,相应的值增加 1,出现在 words 中的单词,每出现一次,相应的值减少 1。示例代码:
// 每一种分组方式的 differ 初始化
for (int i = 0; i < n && i + m * n <= ls; ++i) {unordered_map<string, int> differ;// 每一种分组方式的窗口内 differ ++for (int j = 0; j < m; ++j) {++differ[s.substr(i + j * n, n)];}// 每一种分组方式 words 内 differ --for (string &word: words) {if (--differ[word] == 0) {differ.erase(word);}}
}
然后将窗口右移,右侧会加入一个单词,左侧会移出一个单词,并对 differ 做相应的更新。窗口移动时,若出现 differ 中值不为 0 的键的数量为 0,则表示这个窗口中的单词频次和 words 中单词频次相同,窗口的左端点是一个待求的起始位置。示例代码:
for (int start = i; start < ls - m * n + 1; start += n) {// 以初始化的 differ 为基础进行判断if (start != i) { // start = i 时,直接判断 differ 是否为空,为空则 start = i 是一个起始位置// 先加入一个单词string word = s.substr(start + (m - 1) * n, n);if (++differ[word] == 0) {differ.erase(word);}// 后移除一个单词word = s.substr(start - n, n);if (--differ[word] == 0) {differ.erase(word);}}// 如果 differ 为空,则表示这个窗口中的单词频次和 `words` 中单词频次相同,将当前起始位置加入答案数组if (differ.empty()) {res.emplace_back(start);}
}
总的实现代码
class Solution {
public:vector<int> findSubstring(string &s, vector<string> &words) {vector<int> res;int m = words.size(), n = words[0].size(), ls = s.size();for (int i = 0; i < n && i + m * n <= ls; ++i) {unordered_map<string, int> differ;for (int j = 0; j < m; ++j) {++differ[s.substr(i + j * n, n)];}for (string &word: words) {if (--differ[word] == 0) {differ.erase(word);}}for (int start = i; start < ls - m * n + 1; start += n) {if (start != i) {string word = s.substr(start + (m - 1) * n, n);if (++differ[word] == 0) {differ.erase(word);}word = s.substr(start - n, n);if (--differ[word] == 0) {differ.erase(word);}}if (differ.empty()) {res.emplace_back(start);}}}return res;}
};复杂度分析
时间复杂度: O ( n × m ) O(n \times m) O(n×m), n n n 为 words 中每个单词的长度, m m m 为 s 的长度。
空间复杂度: O ( n × k ) O(n \times k) O(n×k), n n n 为 words 中每个单词的长度, k k k 为 words 的长度,每次滑动窗口时,需要用一个哈希表保存单词频次。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。