蓝桥杯题库简单每日十题 day11

在这里插入图片描述

01 质数

质数
题目描述
给定一个正整数N，请你输出N以内（不包含N）的质数以及质数的个数。
输入描述
输入一行，包含一个正整数N。1≤N≤10^3
输出描述
共两行。
第1行包含若干个素数，每两个素数之间用一个空格隔开，素数从小到大输出。
第2行包含一个整数，表示N以内质数的个数。
输入输出样例
示例
输入

输出

2 3 5 7
4

#include <iostream>
#include<math.h>
using namespace std;
bool isprime(int n){if(n==2) return true;else{for(int i=2;i<=sqrt(n);i++){if(n%i==0) return false;}}return true;
}
int main(){int x,cnt=0; cin>>x;for(int i=2;i<x;i++){if(isprime(i)){cout<<i<<" ";cnt++;}}
cout<<"\n"<<cnt;
return 0;
}

02 字符统计

字符统计
问题描述
给定一个只包含大写字母的字符出S，请你输出其中出现次数最多的字符。
如果有多个字母均出现了最多次，按字母表顺序依次输出所有这些字母。
输入格式
一个只包含大写字母的字等串S.
输出格式
若干个大写字母，代表答案。
样例输入

BABBACAC

样例输出

AB

#include<iostream>
using namespace std;
int main(){string s;getline(cin,s);int b[10000]={0};for(int i=0;i<s.length();i++){b[s[i]]++;}int max=0;for(int i='A';i<='z';i++){if(b[i]>max){max=b[i];}}for(int i='A';i<='z';i++){if(b[i]==max){cout<<char(i);}}return 0;}

03 大乘积

问题描述
小蓝有30个数，分别为：99,22,51,63,72,61,20,88,40,21,63,30,
11, 18, 99, 12, 93, 16, 7, 53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77 。
小蓝可以在这些数中取出两个序号不同的数，共有30×29/2=435种取法。
请问这435种取法中，有多少种取法取出的两个数的乘积大于等于2022。
答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为
一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[])
{int i,k,sum=0;int a[30]={99,22,51,63,72, 61, 20, 88, 40, 21, 63, 30, 11, 18, 99, 12, 93, 16, 7,53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77};
for(i=0;i<30;i++){for(k=i+1;k<30;k++){if(a[i]*a[k]>=2022){sum++;}}
}
printf("%d",sum);
return 0;
}

04 组合数问题

在这里插入图片描述
输入输出样例
示例
输入

1 2
3 3

输出

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;const ll MOD = 1E9 +7;ll t, k;
ll n, m, ans, len;
ll a[70], b[70];
ll dp[70][4];ll ans0(ll x, ll y) {
//    if (x < 0 || y < 0) return 0;if (x <= y) return (x % MOD + 2) * (x % MOD + 1) / 2 % MOD;x %= MOD, y %= MOD;return ((y + 2) * (y + 1) / 2 % MOD + (x - y) * (y + 1) % MOD) % MOD;
}ll ans1(ll x, ll y) {
//    if (x < 0 || y < 0) return 0;return min(x, y) + 1;
}ll ans2(ll x, ll y) {
//    if (x < 0 || y < 0) return 0;return max(x - y + 1, 0LL);
}int main() {cin >> t >> k;while (t--) {cin >> n >> m;if (m > n) m = n;ans = ans0(n, m);memset(b, 0, sizeof b);for (len = 0; n; len++, n /= k) a[len] = n % k;for (int i = 0; m; i++, m /= k) b[i] = m % k;n = len;
//        memset(dp, 0, sizeof dp);dp[n][0] = dp[n][1] = dp[n][2] = 0;dp[n][3] = 1;for (int i = n - 1; i >= 0; i--) {dp[i][0] = dp[i + 1][0] * ans0(k - 1, k - 1);dp[i][0] += dp[i + 1][1] * ans0(a[i] - 1, k - 1) + dp[i + 1][2] * ans0(k - 1,b[i] - 1);dp[i][0] += dp[i + 1][3] * ans0(a[i] - 1, b[i] - 1);dp[i][1] = dp[i + 1][1] * ans1(a[i], k - 1) + dp[i + 1][3] * ans1(a[i], b[i] - 1);dp[i][2] = dp[i + 1][2] * ans2(k - 1, b[i]) + dp[i + 1][3] * ans2(a[i] - 1, b[i]);dp[i][3] = ((a[i] >= b[i]) && dp[i + 1][3]);dp[i][0] %= MOD; dp[i][1] %= MOD;dp[i][2] %= MOD; dp[i][3] %= MOD;}ans -= (dp[0][0] + dp[0][1] + dp[0][2] + dp[0][3]) % MOD;ans = (ans % MOD + MOD) % MOD; cout << ans << endl;}return 0;
}

05 糖果

在这里插入图片描述
输入输出样例
示例
输入

1 2
3 3

输出

 #include<iostream>
using namespace std;
int dp[(1<<20)+1];//dp数组 
int n,m,k,a[101]; 
//状态压缩动态规划（简称状压dp）是另一类非常典型的动态规划，通常使用在NP问题的小规模求解中，虽然是指数级别的复杂度
//该算法主要以二进制的方式 思维 
//入门：https://www.cnblogs.com/ibilllee/p/7651971.html   https://zhuanlan.zhihu.com/p/131585177
int main()
{fill(dp,dp+(1<<20)+1,0xffff);//初始化 dp数组 cin >> n >> m >> k;//输入 int c[m];//占位数组 有则是1 无为0 fill(c,c+m,0);//用来鉴定是否能全尝到 bool NUL=false;//用来鉴定是否能全尝到 for(int i=1;i<=n;++i)//有n包 {int x=0,y;for(int j=1;j<=k;++j)//每包中的 类型 {//比如有5类糖果即5位 二进制0表示没有 1表示有 如果某一组是有 1(1<<1-1=00001) 3(1<<3-1=00100) 4(1<<4-1=01000) 糖果//然后这一组进行 ‘|’ 或运算  然后就可以表示这一组就是 01101 然后这个数字十进制13就可以表示这个 这一包的种类cin >> y; y--;//上面有过程 解释 x|=(1<<y);//或运算是在(十进制也是在二进制中)二进制中 0|1=1 0|0=0 1|1=1 1<<v相当于乘v个2 //根据二进制可以知道有几种糖果c[y]++; //先检验糖果是否全 只和鉴定是否能全得到有关 }a[i]=x;//将每一包所有的种类给它 }for(int i=0;i<m;i++)//用来鉴定是否能全尝到 if(!c[i])NUL=true;//用来鉴定是否能全尝到 if(NUL)cout <<"-1";//糖果种类不全打印-1 else{dp[0]=0;//初始化 当然下面这个肯定从这里开始的 for(int i=1;i<=n;i++){// (1<<m)-1 - > length(1<<n-1) = n = n个(1) - > (1<<m)-1的意义 for(int j=(1<<m)-1;j>=0;--j)//dp[j|a[i]]=min(dp[j|a[i]],dp[j]+1);//从第一包开始  /** 解释：： dp[j|a[i]] 表示在所有糖果类中的 j|a[i] 类中的 最优解① 当j=0 时  j|a[i]=a[i] dp[a[i]]=1;② 当j=a[i1] 时 dp[[j|a[i2]] 就是 a[i1]与a[i2] 并集的 最优解③ 进一步向上迭代 直至完全 ④ 当计算出j|a[i]=(1)n 时（进制全为一 ） 即包含所有种类 这个就是最终解 */ }cout << dp[(1<<m)-1];//打印最终解 } return 0;
}

06 外卖店优先级

在这里插入图片描述
输出描述
输出一个整数代表答案。
输入输出样例
示例
输入

输出

样例解释：
6时刻时，1号店优先级降到3，被移除出优先缓存；2号店优先级升到6，加入优先缓存。所以是有1家店（2号）在优先缓存中。

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int main()
{int num,m,t;cin>>num>>m>>t;pair<int,int> ti[m];//订单列表int p[num]={0};//存优先级int flag[num]={0};//1表示在优先缓存，0表示不在int last[num]={0};//存对应id外卖店的上一次接订单时间int cnt=0;for(int i=0;i<m;i++)cin>>ti[i].first>>ti[i].second;//读取订单列表sort(ti,ti+m);//按时间升序排列订单for(int i=0;i<m;i++)//遍历订单列表{int tt=ti[i].first,id=ti[i].second-1;if(tt!=last[id])//该外卖店在下一个时刻接到了订单p[id]-=tt-last[id]-1;if(p[id]<0)p[id]=0;if(p[id]<=3)flag[id]=0;p[id]+=2;if(p[id]>5)flag[id]=1;last[id]=tt;}for(int i=0;i<num;i++){p[i]-=t-last[i];if(p[i]<=3)flag[i]=0;}int ans=0;for(int i=0;i<num;i++)if(flag[i]==1)ans++;cout<<ans;return 0;
}

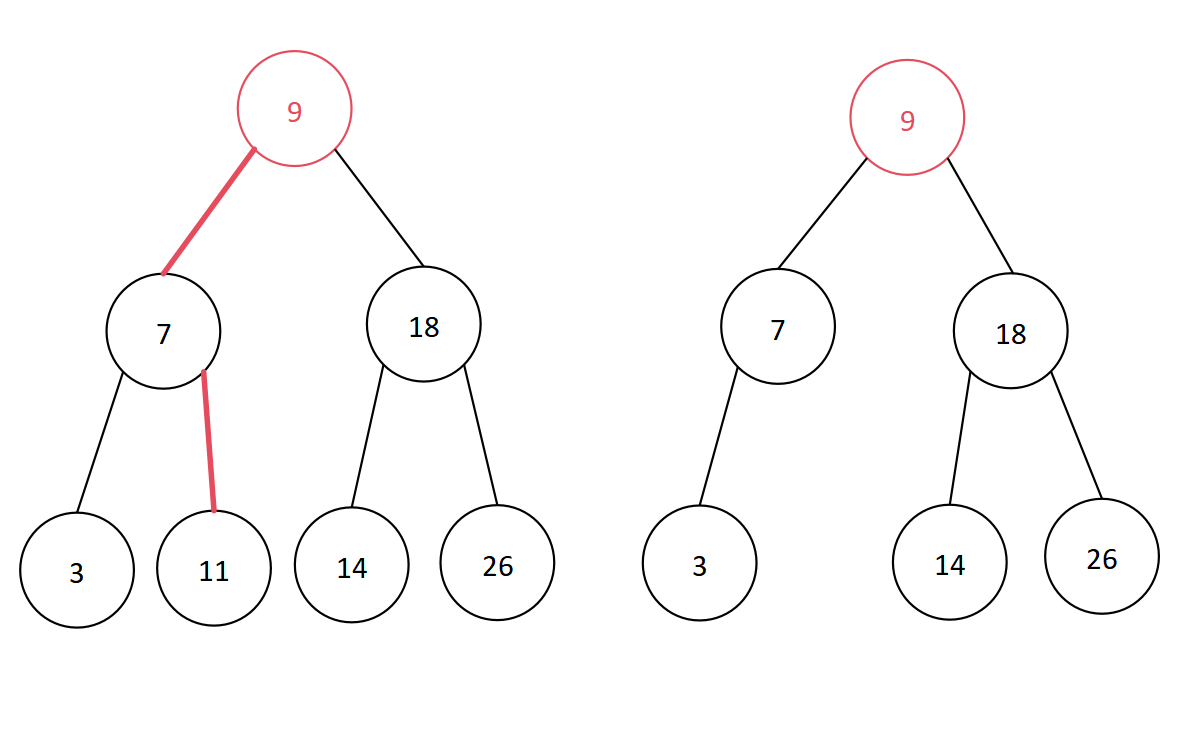
07 完全二叉树的权值

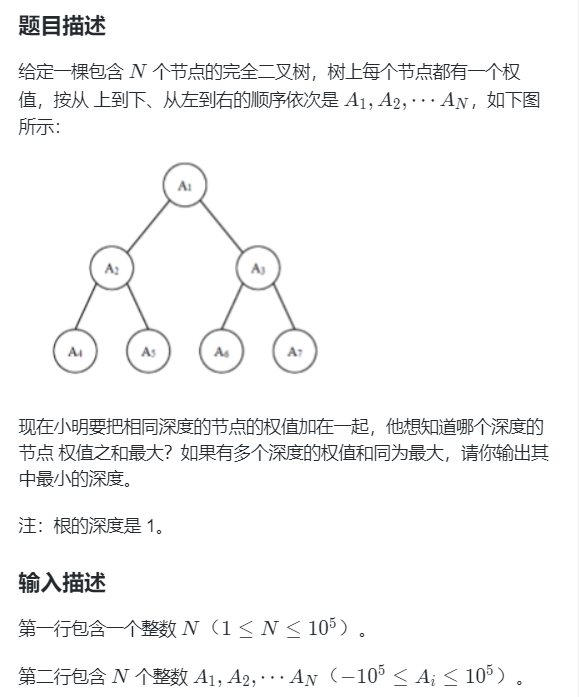
在这里插入图片描述
输出描述
输出一个整数代表答案。
输入输出样例
示例
输入

7
1 6 5 4 3 2 1

输出

#include<bits/stdc++.h>
using namespace std;
int sum[10008] = {0};
int main()
{int n;int w;int ans;int maxn = 0;cin >> n;for(int i = 1; i <= n; i++){cin >> w;int d = ceil(log(i+1)/log(2));sum[d] += w;}for(int i = 1; i < 10008; i++){if(sum[i] > maxn){maxn = sum[i];ans = i;}}cout << ans;return 0;
}

08 修改数组

在这里插入图片描述

输入输出样例
示例
输入

5
2 1 1 3 4

输出

2 1 3 4 5

#include <iostream>
using namespace std;
int main()
{int n;int a[100005]={0}, b[1000005] = { 0 };cin >> n;for (int i = 0; i < n; i++){cin >> a[i];while (b[a[i]] != 0){b[a[i]]++;a[i]+=(b[a[i]]-1);}b[a[i]]++;cout << a[i] << ' ';}return 0;
}

09 小明的背包1

在这里插入图片描述
输入输出样例
示例1
输入

输出

#include <stdio.h>
#include <stdlib.h>
int val[1001],v[1001],dp[1001][1001]={0};//dp第一个为物品下标，第二个为背包体积，值为价值(确定dp数组以及下标的含义)
int n,V;
int max(int a,int b)
{return a>b?a:b;
}
void backpack()
{for(int i=v[0];i<=V;i++){dp[0][i]=val[0];// 当背包容量大于物品0的容量时，将物品0放入到背包中}for(int i=1;i<=n;i++){for(int j=1;j<=V;j++)//先遍历物品，再遍历体积{if(j<v[i])//当前背包体积小于物品体积dp[i][j]=dp[i-1][j];//不放，价值不变，i-1相当于没放物品i之前的else{dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+val[i]);//比较放之前和放之后的价值//放之后的价值=放之前的价值+物品i的价值//j-v[i]表示放了物品i，还剩下j-v[i]的容量可以放其他物品//dp[i-1][j-v[i]]，表示不放物品i时，背包的容量也减去物品i的容量之后，背包所能放的最大价值}}}
}
int main()
{scanf("%d%d",&n,&V);for(int i=0;i<n;i++)scanf("%d %d",&v[i],&val[i]);backpack();printf("%d",dp[n][V]);return 0;
}

10 求阶乘

问题描述
满足N！的末尾恰好有K个0的最小的N是多少？
如果这样的N不存在输出-1。
输入格式
一个整数K。
输出格式
一个整数代表答案。
样例输入

样例输出

在这里插入图片描述

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
//末尾有几个0取决于从1到N的因子中2和5的组合个数
//因为5的倍数个数比2少，所以只要计算5的倍数个数
//满足5^p<=N的个数，复杂度为O(logN),又因为N越大，末尾的0越多，所以可以用二分找到答案
//此函数用于计算因子5的个数
long long int js( long long int a )
{long long int ans = 0;while ( a > 0 ){ans += a / 5; //因为遇见 5^2要加两个0 5^3要加三个零 以此类推a/=5;}return ans;
}
int main(int argc, char *argv[])
{long long int k;scanf("%lld",&k);long long int l = 1, r = pow(2,63)-1;//pow(2,63)-1表示N的最大值//从1到N的阶乘中5的倍数个数计算出来，再用与k比较的二分法查找出最小的N！while(l<r){long long int mid = l + ( r - l ) / 2;if ( js(mid) < k ) l = mid + 1;else r = mid;}long long int ans = js(l);if ( ans == k ) printf("%lld",l);//如果找到打印，否则打印-1；else printf("%d",-1);// 请在此输入您的代码return 0;
}