什么是数学建模
前提:我们数学建模国赛计划选择C题,故希望老师的教学中侧重与C题相关性大的模型及其思想进行培训。之后的学习内容中希望涉及以下知识点:
- logistic回归相关知识点。如:用法、适用、限制范围等。
- 精学数学建模中常用的两种不同的机器学习方法。顺带,不同机器学习方法的适用侧重点如预测、分类等。
- 统计学中模型检验相关。(上课时学校老师提了一句“应用统计学的方法一定要进行模型检验”没明白这个有什么例子可以辅助理解)。
总领
专业支持领域: 中国工业与应用数学协会(CSIAM),李大潜院士为其理事长

行业OG:

什么是数学建模
答:为考察的实际问题建立数学模型。
交叉学科:

数学技术=数学+计算机

数学建模的发展:
《欧几里得几何原本》:数学方法演绎推理。
开普勒行星运动三大规律,牛顿总结得出的万有引力公式。

数学建模对发展数学学科和

所以,我们也可以发现,现在数学建模A类赛题也更加偏向于物理竞赛,考察偏微分方程的应用和求解。

苏德矿、?(外国一教授)、数学建模竞赛官方老师(?)
《数学》


是一种 空间形式 和 数量关系 上的抽象。


对数学建模的学习与训练的建立
学习若干个典例,就能对数学建模有所认识。

跳学,选学。
案例式教学。


即,同一问题的多种不同的解法,再看解法的优劣,进行对比学习。
数学建模的特点:

即:在广不在深。

做中学

数学建模–现实模型的简化

“三脚架” 的比喻:

马尔萨斯《人口论》
一种数学模型的分类

logistics模型
微分方程离散化:差分方程
多了一个参数的参与,将常数替换为函数。
发现趋于混沌的规律
Leslie模型
增添更多的参数,使得模型更加的复杂。

火箭为什么是三级
考虑问题:

聚焦问题:

问题的递进:

层层递进的作用。
投资如何优化策略
众多资产品种:

投资要解决的基本矛盾:

投资组合选择模型
理论:

概率论的相关知识:

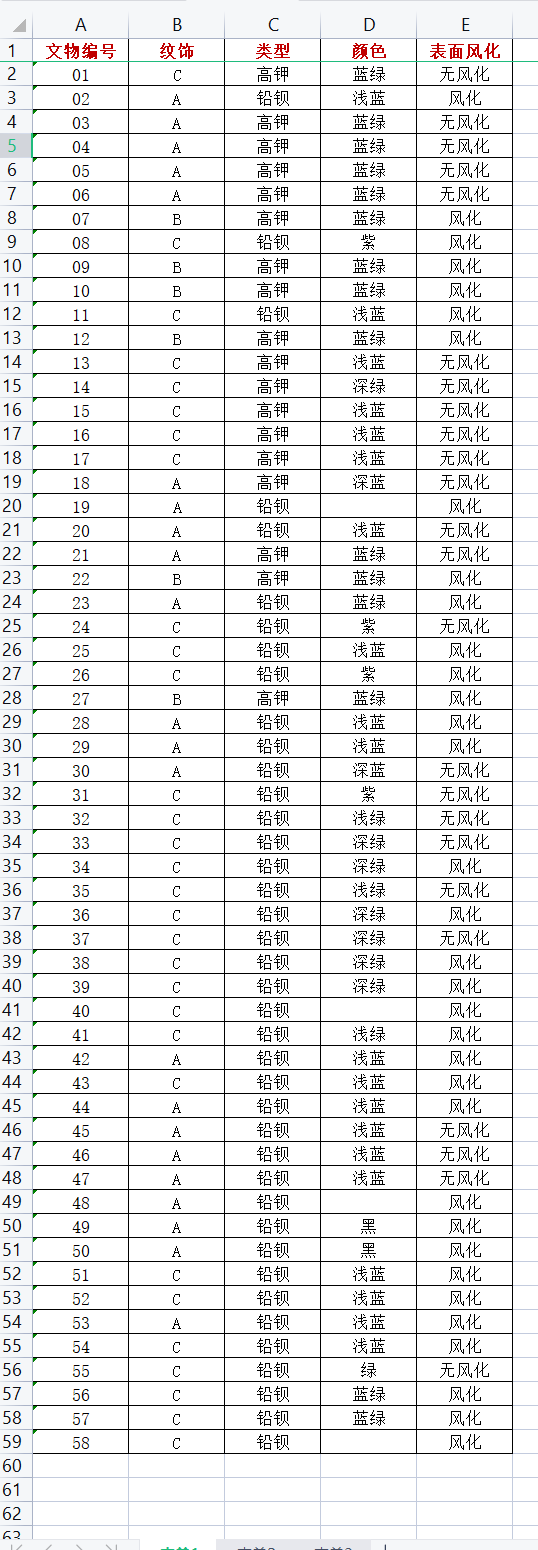
2022C 玻璃成分分析
统计学的适用范围


数据: