文章目录
- 1. LeNet历史背景
- 1.1 早期神经网络的挑战
- 1.2 LeNet的诞生背景
- 2. LeNet详细结构
- 2.1 总览
- 2.2 卷积层与其特点
- 2.3 子采样层(池化层)
- 2.4 全连接层
- 2.5 输出层及激活函数
- 3. LeNet实战复现
- 3.1 模型搭建model.py
- 3.2 训练模型train.py
- 3.3 测试模型test.py
- 4. LeNet的变种与实际应用
- 4.1 LeNet-5及其优化
- 4.2 从LeNet到现代卷积神经网络
1. LeNet历史背景
1.1 早期神经网络的挑战
早期神经网络面临了许多挑战。首先,它们经常遇到训练难题,例如梯度消失和梯度爆炸,特别是在使用传统激活函数如sigmoid或tanh时。另外,当时缺乏大规模、公开的数据集,导致模型容易过拟合并且泛化性能差。再者,受限于当时的计算资源,模型的大小和训练速度受到了很大的限制。最后,由于深度学习领域还处于萌芽阶段,缺少许多现代技术来优化和提升模型的表现。
1.2 LeNet的诞生背景
LeNet的诞生背景是为了满足20世纪90年代对手写数字识别的实际需求,特别是在邮政和银行系统中。Yann LeCun及其团队意识到,对于图像这种有结构的数据,传统的全连接网络并不是最佳选择。因此,他们引入了卷积的概念,设计出了更适合图像处理任务的网络结构,即LeNet。
2. LeNet详细结构
2.1 总览
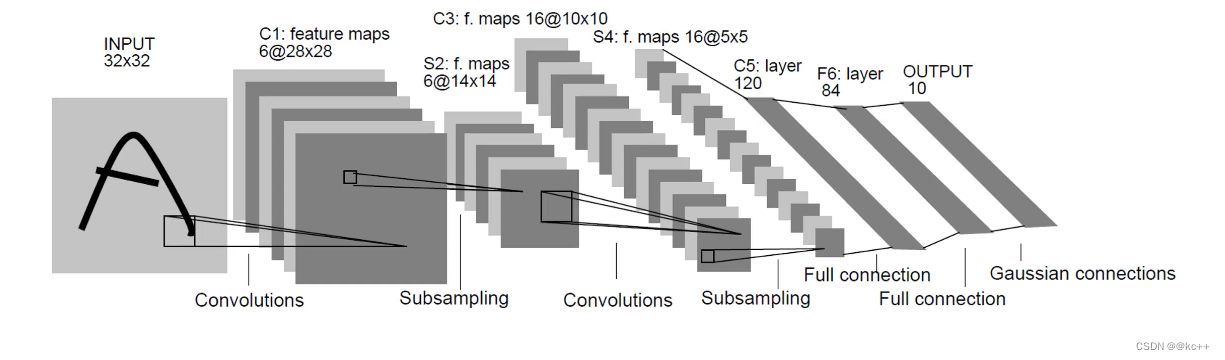
2.2 卷积层与其特点
卷积层是卷积神经网络(CNN)的核心。这一层的主要目的是通过卷积操作检测图像中的局部特征。
特点:
- 局部连接性: 卷积层的每个神经元不再与前一层的所有神经元相连接,而只与其局部区域相连接。这使得网络能够专注于图像的小部分,并检测其中的特征。
- 权值共享: 在卷积层中,一组权值在整个输入图像上共享。这不仅减少了模型的参数,而且使得模型具有平移不变性。
- 多个滤波器: 通常会使用多个卷积核(滤波器),以便在不同的位置检测不同的特征。
2.3 子采样层(池化层)
池化层是卷积神经网络中的另一个关键组件,用于缩减数据的空间尺寸,从而减少计算量和参数数量。
主要类型:
- 最大池化(Max pooling): 选择覆盖区域中的最大值作为输出。
- 平均池化(Average pooling): 计算覆盖区域的平均值作为输出。
2.4 全连接层
在卷积神经网络的最后,经过若干卷积和池化操作后,全连接层用于将提取的特征进行“拼接”,并输出到最终的分类器。
特点:
- 完全连接: 全连接层中的每个神经元都与前一层的所有神经元相连接。
- 参数量大: 由于全连接性,此层通常包含网络中的大部分参数。
- 连接多个卷积或池化层的特征: 它的主要目的是整合先前层中提取的所有特征。
2.5 输出层及激活函数
输出层:
输出层是神经网络的最后一层,用于输出预测结果。输出的数量和类型取决于特定任务,例如,对于10类分类任务,输出层可能有10个神经元。
激活函数:
激活函数为神经网络提供了非线性,使其能够学习并进行复杂的预测。
- Sigmoid: 取值范围为(0, 1)。
- Tanh: 取值范围为(-1, 1)。
- ReLU (Rectified Linear Unit): 最常用的激活函数,将所有负值置为0。
- Softmax: 常用于多类分类的输出层,它返回每个类的概率。
3. LeNet实战复现
3.1 模型搭建model.py
import torch
from torch import nn# 自定义网络模型
class LeNet(nn.Module):# 1. 初始化网络(定义初始化函数)def __init__(self):super(LeNet, self).__init__()# 定义网络层self.Sigmoid = nn.Sigmoid()self.c1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2)self.s2 = nn.AvgPool2d(kernel_size=2, stride=2)self.c3 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)self.s4 = nn.AvgPool2d(kernel_size=2, stride=2)self.c5 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5)# 展开self.flatten = nn.Flatten()self.f6 = nn.Linear(120, 84)self.output = nn.Linear(84, 10)# 2. 前向传播网络def forward(self, x):x = self.Sigmoid(self.c1(x))x = self.s2(x)x = self.Sigmoid(self.c3(x))x = self.s4(x)x = self.c5(x)x = self.flatten(x)x = self.f6(x)x = self.output(x)return xif __name__ == "__main__":x = torch.rand([1, 1, 28, 28])model = LeNet()y = model(x)
3.2 训练模型train.py
import torch
from torch import nn
from model import LeNet
from torch.optim import lr_scheduler
from torchvision import datasets, transforms
import os# 数据转换为tensor格式
data_transformer = transforms.Compose([transforms.ToTensor()
])# 加载训练的数据集
train_dataset = datasets.MNIST(root='./data', train=True, transform=data_transformer, download=True)
train_dataloader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=16, shuffle=True)# 加载测试的数据集
test_dataset = datasets.MNIST(root='./data', train=False, transform=data_transformer, download=True)
test_dataloader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=16, shuffle=True)# 使用GPU进行训练
device = "cuda" if torch.cuda.is_available() else "cpu"# 调用搭好的模型,将模型数据转到GPU上
model = LeNet().to(device)# 定义一个损失函数(交叉熵损失)
loss_fn = nn.CrossEntropyLoss()# 定义一个优化器
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)# 学习率每隔10轮, 变换原来的0.1
lr_scheduler = lr_scheduler.StepLR(optimizer, step_size=10, gamma=0.1)# 定义训练函数
def train(dataloader, model, loss_fn, optimizer):loss, current, n = 0.0, 0.0, 0for batch, (x, y) in enumerate(dataloader):# 前向传播x, y = x.to(device), y.to(device)output = model(x)cur_loss = loss_fn(output, y)_, pred = torch.max(output, axis=1)cur_acc = torch.sum(y == pred)/output.shape[0]optimizer.zero_grad()cur_loss.backward()optimizer.step()loss += cur_loss.item()current += cur_acc.item()n = n + 1print("train_loss" + str(loss/n))print("train_acc" + str(current/n))# 定义测试函数
def val(dataloader, model, loss_fn):model.eval()loss, current, n = 0.0, 0.0, 0with torch.no_grad():for batch, (x, y) in enumerate(dataloader):# 前向传播x, y = x.to(device), y.to(device)output = model(x)cur_loss = loss_fn(output, y)_, pred = torch.max(output, axis=1)cur_acc = torch.sum(y == pred) / output.shape[0]loss += cur_loss.item()current += cur_acc.item()n = n + 1print("val_loss" + str(loss / n))print("val_acc" + str(current / n))return current/n# 开始训练
epoch = 50
min_acc = 0for t in range(epoch):print(f'epoch{t+1}\n-----------------------------------------------------------')train(train_dataloader, model, loss_fn, optimizer)a = val(test_dataloader, model, loss_fn)# 保存最好的模型权重if a > min_acc:folder = "sava_model"if not os.path.exists(folder):os.mkdir("sava_model")min_acc = aprint("sava best model")torch.save(model.state_dict(), 'sava_model/best_model.pth')
print('Done!')3.3 测试模型test.py
import torch
from model import LeNet
from torchvision import datasets, transforms
from torchvision.transforms import ToPILImage# 数据转换为tensor格式
data_transformer = transforms.Compose([transforms.ToTensor()
])# 加载训练的数据集
train_dataset = datasets.MNIST(root='./data', train=True, transform=data_transformer, download=True)
train_dataloader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=16, shuffle=True)# 加载测试的数据集
test_dataset = datasets.MNIST(root='./data', train=False, transform=data_transformer, download=True)
test_dataloader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=16, shuffle=True)# 使用GPU进行训练
device = "cuda" if torch.cuda.is_available() else "cpu"# 调用搭好的模型,将模型数据转到GPU上
model = LeNet().to(device)# 加载模型权重并设置为评估模式
model.load_state_dict(torch.load("./sava_model/best_model.pth"))
model.eval()# 获取结果
classes = ["0","1","2","3","4","5","6","7","8","9",
]# 把tensor转换为图片, 方便可视化
show = ToPILImage()# 进入验证
for i in range(5):x, y = test_dataset[i]show(x).show()x = torch.unsqueeze(x, dim=0).float().to(device)with torch.no_grad():pred = model(x)predicted, actual = classes[torch.argmax(pred[0])], classes[y]print(f'Predicted: {predicted}, Actual: {actual}')4. LeNet的变种与实际应用
4.1 LeNet-5及其优化
LeNet-5是由Yann LeCun于1998年设计的,并被广泛应用于手写数字识别任务。它是卷积神经网络的早期设计之一,主要包含卷积层、池化层和全连接层。
结构:
- 输入层:接收32×32的图像。
- 卷积层C1:使用5×5的滤波器,输出6个特征图。
- 池化层S2:2x2的平均池化。
- 卷积层C3:使用5×5的滤波器,输出16个特征图。
- 池化层S4:2x2的平均池化。
- 卷积层C5:使用5×5的滤波器,输出120个特征图。
- 全连接层F6。
- 输出层:10个单元,对应于0-9的手写数字。
激活函数:Sigmoid或Tanh。
优化:
- ReLU激活函数: 原始的LeNet-5使用Sigmoid或Tanh作为激活函数,但现代网络更喜欢使用ReLU,因为它的训练更快,且更少受梯度消失的影响。
- 更高效的优化算法: 如Adam或RMSProp,它们通常比传统的SGD更快、更稳定。
- 批量归一化: 加速训练,并提高模型的泛化能力。
- Dropout: 在全连接层中引入Dropout可以增强模型的正则化效果。
4.2 从LeNet到现代卷积神经网络
从LeNet-5开始,卷积神经网络已经经历了巨大的发展。以下是一些重要的里程碑:
- AlexNet (2012): 在ImageNet竞赛中取得突破性的成功。它具有更深的层次,使用ReLU激活函数,以及Dropout来防止过拟合。
- VGG (2014): 由于其统一的结构(仅使用3×3的卷积和2x2的池化)而闻名,拥有多达19层的版本。
- GoogLeNet/Inception (2014): 引入了Inception模块,可以并行执行多种大小的卷积。
- ResNet (2015): 引入了残差块,使得训练非常深的网络变得可能。通过这种方式,网络可以达到上百甚至上千的层数。
- DenseNet (2017): 每层都与之前的所有层连接,导致具有非常稠密的特征图。