目录
- 一、单源最短路径
- 1.1 算法基本思想
- 1.2 算法设计思想
- 1.3 算法的正确性和计算复杂性
- 1.4 归纳证明思路
- 1.5 归纳步骤证明
- 二、最小生成树
- 2.1 最小生成树性质
- 2.1.1 生成树的性质
- 2.1.2 生成树性质的应用
- 2.2 Prim算法
- 2.2.1 正确性证明
- 2.2.2 归纳基础
- 2.2.3 归纳步骤
- 2.3 Kruskal算法
- 2.3.1 证明思路
- 2.3.2 归纳步骤证明
- 2.3.3 T是G的最小生成树
- 2.4 应用:数据分组问题
- 2.5 单链聚类
- 三、多机调度问题
- 四、小结
一、单源最短路径
给定带权有向图G =(V,E),其中每条边的权是非负实数。另外,还给定V中的一个顶点,称为源。现在 要计算从源到所有其它各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。
1.1 算法基本思想
Dijkstra算法是解单源最短路径问题的贪心算法。
Dijkstra算法有关概念:
X∈S←→x∈V且从s到x的最短路径已经找到
初始:S={s},S=V时算法结束
从s到u相对于S的最短路径:从s到u且经过S中顶点的最短路径
dist[u]:从s到u相对S最短路径的长度
short[u]:从s到u的最短路径的长度
dist[u]>=short[u]
1.2 算法设计思想
输入:有向图G=(V,E),V={1,2,…,n},s=1
输出:从s到每个顶点的最短路径
1.初始S={1}
2.对于i∈V-S,计算1到i的相对S的最短路,长度dist[i],没有路可记为∞或maxint
3.选择V-S中dist值最小的j,将j加入S,修改V-S中顶点的dist值
4.继续上述过程,直到S=V为止
其基本思想是,设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时,S中仅含有源。设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist作必要的修改。一旦S包含了所有V中顶点,dist就记录了从源到所有其它顶点之间的最短路径长度。
例如,对 右图中的有向图,应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下页的表中。
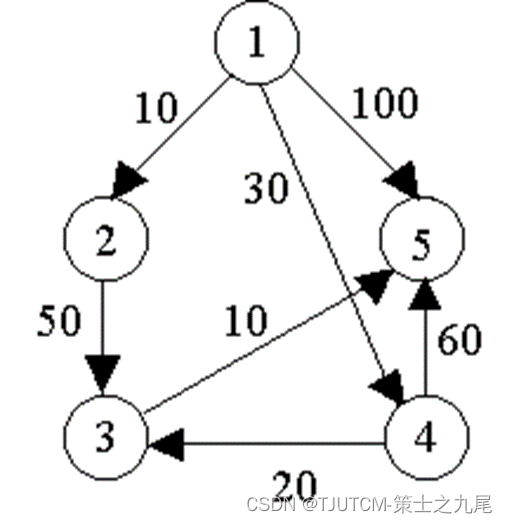
Dijkstra算法的迭代过程:

1.3 算法的正确性和计算复杂性
(1)贪心选择性质
(2)最优子结构性质
(3)计算复杂性
对于具有n个顶点和e条边的带权有向图,如果用带权邻接矩阵表示这个图,那么Dijkstra算法的主循环体 需要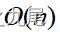 时间。这个循环需要执行n-1次,所以完成循环需要
时间。这个循环需要执行n-1次,所以完成循环需要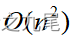 时间。算法的其余部分所需要时间不超过
时间。算法的其余部分所需要时间不超过 。
。
1.4 归纳证明思路
命题:当算法进行到第k步时,对于S中每个结点i,dist[i]=short[i]
归纳基础
k=1,S={s},dist[s]=short[s]=0
归纳步骤
证明:假设命题对k为真,则对k+1命题也为真
1.5 归纳步骤证明
假设命题对k为真,考虑k+1步算法选择顶点v(边<u,v>)。需要证明dist[v]=short[v]
若存在另一条s-v路径L,最后一次出S的顶点为x,经过V-s的第一个顶点y,再由y经过一段在V-S中的路径到达v

二、最小生成树
设G =(V,E)是无向连通带权图,即一个网络。E中每条边(v,w)的权为c[v][w]。如果G的子图G’是一棵包含G的所有顶点的树,则称G’为G的生成树。生成树上各边权的总和称为该生成树的耗费。在G的所有生成树中,耗费最小的生成树称为G的最小生成树。
网络的最小生成树在实际中有广泛应用。例如,在设计通信网络时,用图的顶点表示城市,用边(v,w)的权c[v][w]表示建立城市v和城市w之间的通信线路所需的费用,则最小生成树就给出了建立通信网络的最经济的方案。
2.1 最小生成树性质
用贪心算法设计策略可以设计出构造最小生成树的有效算法。本节介绍的构造最小生成树的Prim算法和Kruskal算法都可以看作是应用贪心算法设计策略的例子。尽管这2个算法做贪心选择的方式不同,它们都利用了下面的最小生成树性质:
设G=(V,E)是连通带权图,U是V的真子集。如果(u,v)E,且uU,vV-U,且在所有这样的边中,(u,v)的权c[u][v]最小,那么一定存在G的一棵最小生成树,它以(u,v)为其中一条边。这个性质有时也称为MST性质。
2.1.1 生成树的性质
设G是n阶连通图,那么
T是G的生成树,当且仅当T无圈且有n-1条边。
如果T是G的生成树,e不属于T那么T∪{e}含有一个圈C(回路)。
去掉圈C的任意一条边,就得到G的另一棵生成树T’。
2.1.2 生成树性质的应用
算法步骤:选择边
约束条件:不形成回路
截止条件:边数达到n-1
改进生成树T的方法:
在T中加一条非树边e,形成回路C,在C中去掉一条树边ei,形成一颗新的生成树T’
W(T’)-W(T)=W(e)-W(ei)
若W(e)<=W(ei),则 W(T’)<=W(T)
2.2 Prim算法
设G=(V,E)是连通带权图,V={1,2,…,n}。
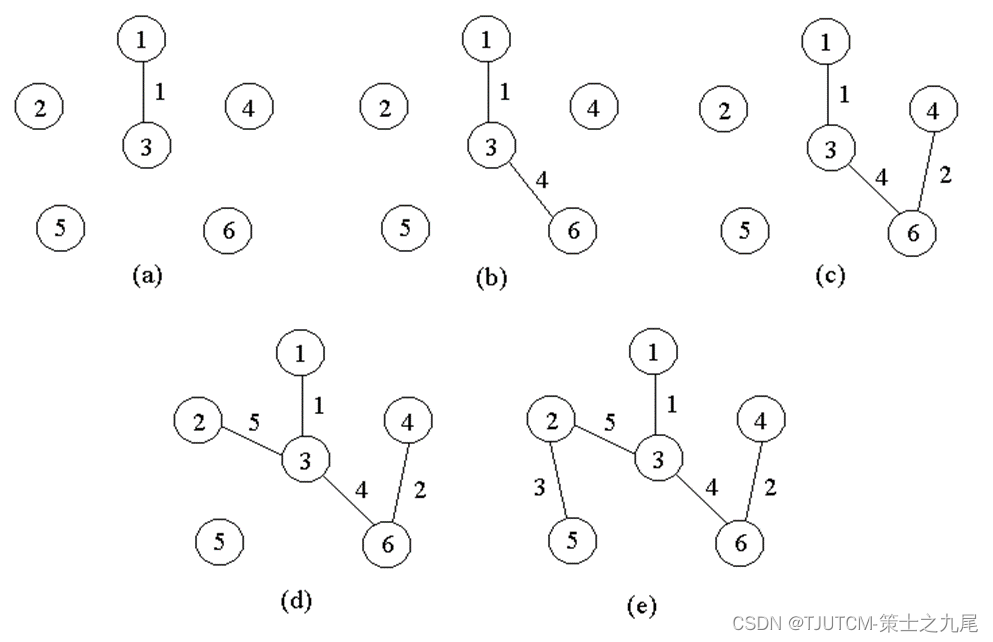
构造G的最小生成树的Prim算法的基本思想是:首先置S={1},然后,只要S是V的真子集,就作如下的贪心选择:选取满足条件iS,jV-S,且c[i][j]最小的边,将顶点j添加到S中。这个过程一直进行到S=V时为止。
在这个过程中选取到的所有边恰好构成G的一棵最小生成树。
利用最小生成树性质和数学归纳法容易证明,上述算法中的边集合T始终包含G的某棵最小生成树中的边。因此,在算法结束时,T中的所有边构成G的一棵最小生成树。
例如,对于右图中的带权图,按Prim算法选取边的过程如下页图所示。
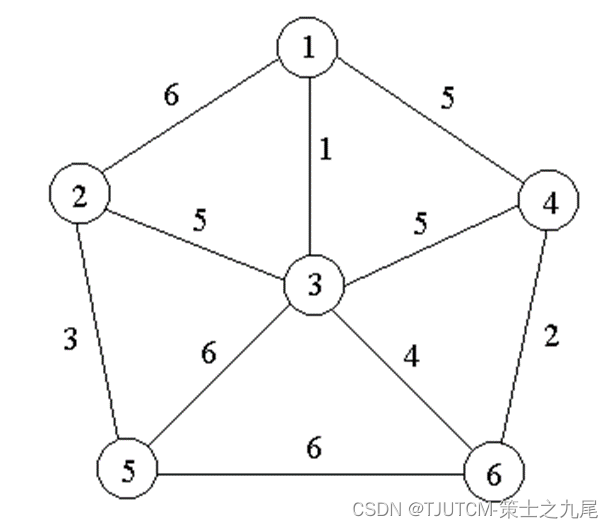
2.2.1 正确性证明
命题:对于任意k<n,存在一棵最小生成树包含算法前k步选择的边。
归纳基础:k=1,存在一棵最小生成树T包含边e={1,i},其中 {1,i}是所有关联1的边中权最小的。
归纳步骤:假设算法前k步选择的边构成一棵最小生成树的边,则算法前k+1步选择的边也构成一棵最小生成树的边。
2.2.2 归纳基础
证明:存在一棵最小生成树T包含关联结点1的最小权的边e={1,i}
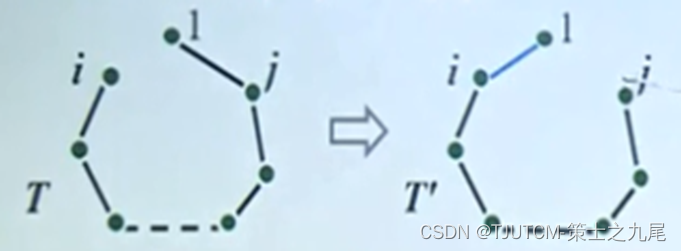
证:设T为一棵最小生成树,假设T不包含{1,i},则T∪ {1,i}含有一条回路,回路中关联1的另一条边{1,j}。用{1,i} 替换{1,j}得到树T’,则T’也是生成树,且W(T’)<=W(T)
2.2.3 归纳步骤
假设算法进行了k步,生成树的边为e1,e2,…ek,这些边的端点构成集合S。由归纳假设存在G的一棵最小生成树T包含这些边
算法第k+1步选择顶点ik+1,则ik+1到S中顶点边权最小,设此边ek+1={ik+1,il},若ek+1∈T,算法k+1步显然正确
假设T不含有ek+1,则将ek+1加到T中形成一条回路。这条回路有另外一条中顶点的边e连接S与V-S中顶点的边e,
令T*=(T-{e})∪{ek+1}则T是G的一棵生成树,包含e1,e2,…ek+1,且W(T)<=W(T)算法到k+1步仍得到最小生成树

在上述Prim算法中,还应当考虑如何有效地找出满足条件iS,jV-S,且权c最小的边(i,j)。实现这个目的的较简单的办法是设置2个数组closest和lowcost。
在Prim算法执行过程中,先找出V-S中使lowcost值最小的顶点j,然后根据数组closest选取边(j,closest[j]),最后将j添加到S中,并对closest和lowcost作必要的修改。
用这个办法实现的Prim算法所需的计算时间为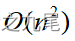 。
。
2.3 Kruskal算法
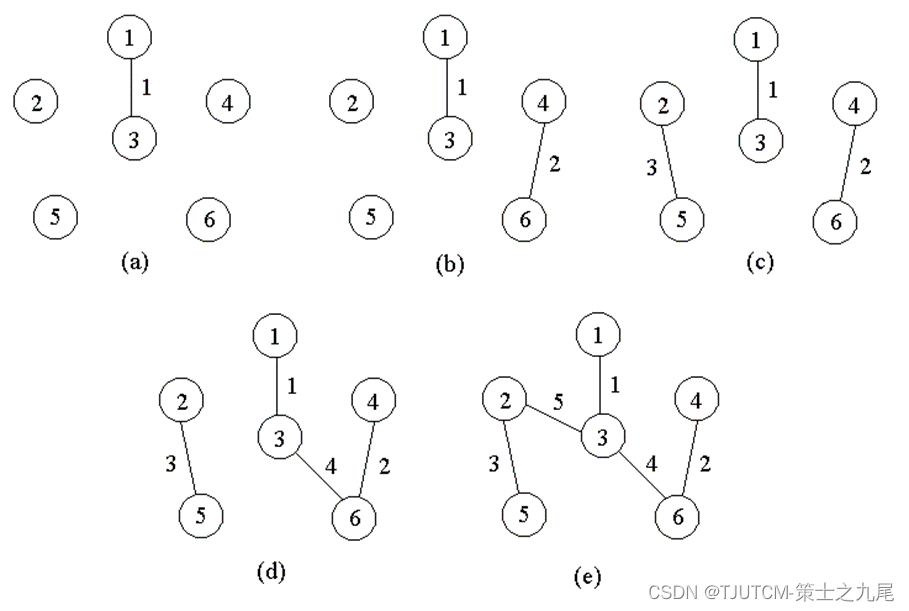
Kruskal算法构造G的最小生成树的基本思想是,首先将G的n个顶点看成n个孤立的连通分支。将所有的边按权从小到大排序。然后从第一条边开始,依边权递增的顺序查看每一条边,并按下述方法连接2个不同的连通分支:当查看到第k条边(v,w)时,如果端点v和w分别是当前2个不同的连通分支T1和T2中的顶点时,就用边(v,w)将T1和T2连接成一个连通分支,然后继续查看第k+1条边;如果端点v和w在当前的同一个连通分支中,就直接再查看第k+1条边。这个过程一直进行到只剩下一个连通分支时为止。
例如,对前面的连通带权图,按Kruskal算法顺序得到的最小生成树上的边如下图所示。
命题:对于任意n,算法对n阶图找到一棵最小生成树。
2.3.1 证明思路
归纳基础 证明:n=2,算法正确。G只有一条边,最小生成树就是G
归纳步骤 证明:假设算法对于n阶图是正确的,其中n>1,则对于任何n+1阶图算法也得到一棵最小生成树
短接操作:任意给n+1个顶点的图G,G中最小边的权e={i,j},从G中合并i和j,得到图G’
2.3.2 归纳步骤证明
对于任意n+1阶图G短接最短边e,得到n阶图G’
根据归纳假设算法得到G’的最小生成树T’
将被短接的边e“拉伸”回到原来长度,得到树T
证明T是G的最小生成树
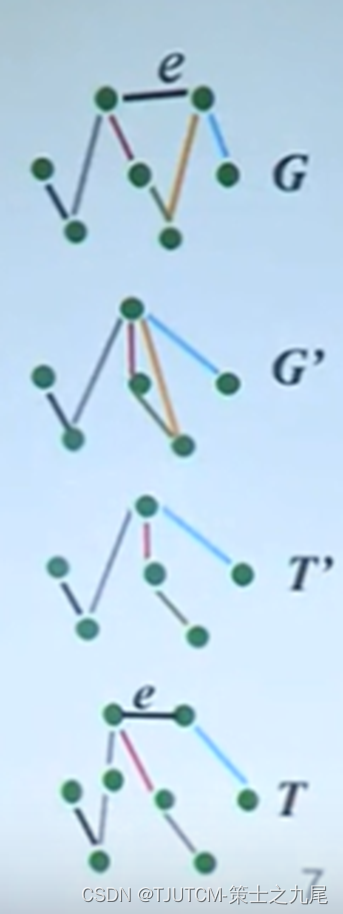
2.3.3 T是G的最小生成树
T=T’∪{e}是关于G的最小生成树
否则存在G的含边e的最小生成树
T*,W(T*)<W(T)。(如果e不属于T*,在T中加边e,形成回路。去掉回路中任意别的边 所得生成树的权仍旧最小)在T短接e得到G’的生成树T*-{e},
W(T*-{e})=W(T*)-w(e)<W(T)-w(e)=W(T’),与T’的最优性矛盾
关于集合的一些基本运算可用于实现Kruskal算法。
按权的递增顺序查看等价于对优先队列执行removeMin运算。可以用堆实现这个优先队列。
对一个由连通分支组成的集合不断进行修改,需要用到抽象数据类型并查集UnionFind所支持的基本运算。
当图的边数为e时,Kruskal算法所需的计算时间是: 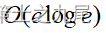 。当
。当 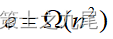 时,Kruskal算法比Prim算法差,但当
时,Kruskal算法比Prim算法差,但当 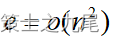 时,Kruskal算法却比Prim算法好得多。
时,Kruskal算法却比Prim算法好得多。
2.4 应用:数据分组问题
一组数据(照片、文件等)要把它们按照相关性进行分类
用相似度函数或者“距离”来描述个体之间的差异
分成几类?使得每类内部的个体尽可能相近,不同类之间的个体尽可能地“远离”。如何划分?
2.5 单链聚类
类似于Kruskal算法。
按照边长从小到大对边排序
依次考察当前最短边e,如果e与已经选中的边不构成回路,则把e加入集合,否则跳过e。记数图的连通分支个数
直到保留了k个连通分支为止
三、多机调度问题
多机调度问题要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。
约定,每个作业均可在任何一台机器上加工处理,但未完工前不允许中断处理。作业不能拆分成更小的子作业。
这个问题是NP完全问题,到目前为止还没有有效的解法。对于这一类问题,用贪心选择策略有时可以设计出较好的近似算法。
采用最长处理时间作业优先的贪心选择策略可以设计出解多机调度问题的较好的近似算法。
按此策略,当  时,只要将机器i的[0, ti]时间区间分配给作业i即可,算法只需要O(1)时间。
时,只要将机器i的[0, ti]时间区间分配给作业i即可,算法只需要O(1)时间。
当 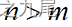 时,首先将n个作业依其所需的处理时间从大到小排序。然后依此顺序将作业分配给空闲的处理机。算法所需的计算时间为O(nlogn)。
时,首先将n个作业依其所需的处理时间从大到小排序。然后依此顺序将作业分配给空闲的处理机。算法所需的计算时间为O(nlogn)。
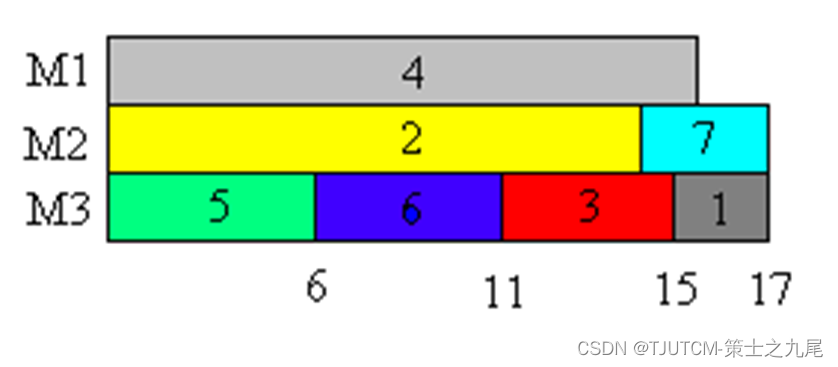
例如,设7个独立作业{1,2,3,4,5,6,7}由3台机器M1,M2和M3加工处理。各作业所需的处理时间分别为{2,14,4,16,6,5,3}。按算法greedy产生的作业调度如下图所示,所需的加工时间为17。
四、小结
贪心算法 通常用来求最优解
总是在当前情况下选择局部最优解,依次进行下去得到整体最优解。
当前最佳选择通常是很容易找到的
贪心算法必须进行正确性证明,一般使用数学归纳法
第一步是显然的
归纳步骤通常使用反证法证明,举反例证伪。