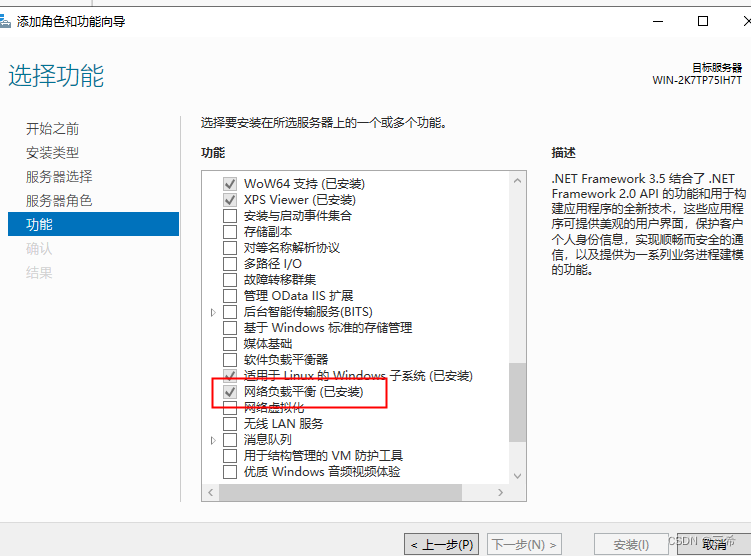
医疗图像其中两种图像格式：MRI（Magnetic Resonance Imaging，磁共振成像）、CT（Computed Tomography，计算机断层），常存成 .nii.gz 格式。都是 3D 的 $H\times W\times L$，但不是 RGB，而是类似 grey-scale 图只有一个 channel，如 CT 的值可能是 Hu 值，取值范围可从负几千到正几千，参考 [1]。segmentation label 也相应是 3D 的。

这里记录几种分割指标，参考 [2,3]，可调 medpy 的包，其文档也有指标列表。记有 C + 1 个类，0 固定是 background，（某个数据的）prediction 和 label Y ^ , Y ∈ { 0 , … , C } H × W × L \hat{Y},Y\in \{0, \dots, C\}^{H \times W \times L} Y^,Y∈{0,…,C}H×W×L，只留下第 c 类的 binary prediction 和 label 为 B ^ c , B c ∈ { 0 , 1 } H × W × L \hat{B}^c,B^c \in \{0, 1\}^{H \times W \times L} B^c,Bc∈{0,1}H×W×L，$|\cdot |$ 表示非零元素个数，${\hat{B}}^c,B^c$ 的 surface / boundray 记为 ${\hat{S}}^c,S^c$，是其表面 voxels 的三维索引向量（下标）的集合。

Dice Coefficient

即 F1-scoure^[2]。第 c 类的 dice 系数：$$D{C}_c=\frac{2|{\hat{B}}^c\cap B^c|}{|{\hat{B}}^c|+|B^c|}$$ 调包：medpy.metric.binary.dc。

IoU

即 Jaccard 系数^[2]。第 c 类的 IoU：$$Io{U}_c=\frac{|{\hat{B}}^c\cap B^c|}{|{\hat{B}}^c\cup B^c|}$$ 调包：medpy.metric.binary.jc。由 [3]，IoU 与 dice 系数有确定的转换关系，即等价，所以两者应该用其中一种就行。C 类的 IoU 取平均就是 mIoU：$$mIoU=\frac{{\sum }_{c=1}^{C}Io{U}_c}{C}$$（2023.9.28：不确定算 mIOU 时要不要加上 background）

Sensitivity

即 recall，也叫 TPR（True Positive Rate），非对称。第 c 类的 sensitivity：$$R_c=\frac{|{\hat{B}}^c\cap B^c|}{|B^c|}$$ 调包：medpy.metric.binary.sensitivity 或 medpy.metric.binary.recall。

Specificity

也叫 selectivity、TNR（True Negative Rate），是 sensitivity 的补。第 c 类的 specifity：$$S{P}_c=\frac{|(1-{\hat{B}}^c)\cap (1-B^c)|}{|(1-B^c)|}$$ 调包：medpy.metric.binary.specificity。

Average (Symmetric) Surface Distance

由 [4]，第 c 类的 average surface distance：$$ASD({\hat{S}}^c,S^c)=\sum _{p\in {\hat{S}}_p^c}{d}_s(p,S^c)/|{\hat{S}}^c|$$ 其中 $d_s(\cdot ,\cdot )$ 是点到点集（此处是表面 S）距离：$$d_s(p,S)=\underset{q\in S}{\min }d(p,q)$$ p , q ∈ { 1 , … , W } × { 1 , … , H } × { 1 , … , L } p,q \in \{1,\dots,W\} \times \{1,\dots,H\} \times \{1,\dots,L\} p,q∈{1,…,W}×{1,…,H}×{1,…,L} 是三维索引向量（下标），$d(\cdot ,\cdot )$ 是欧氏距离。就是对 $\hat{S}$ 中属于此 object 表面的每一个 voxel，都算一下它到 S 的距离，然后取平均。调包：medpy.metric.binary.asd。

ASD 不对称，一般会用 ASSD：$$ASSD({\hat{S}}^c,S^c)=\frac{ASD({\hat{S}}^c,S^c)+ASD(S^c,{\hat{S}}^c)}{2}$$ 调包：medpy.metric.binary.assd。有些文章也会将 ASSD 简叫成 ASD，感觉可以无脑只用 ASSD。

Hausdorff Distance

由 [2,4]，第 c 类的 Hausdorff 距离：$$HD({\hat{S}}^c,S^c)=\max \left\{\underset{p\in {\hat{S}}^c}{\sup }{d}_s(p,S^c),\underset{p\in S^c}{\sup }{d}_s(p,{\hat{S}}^c)\right\}$$ 调包：medpy.metric.binary.hd。

Code

• 分割模型应该一般 predict 的都是 (C+1)-way softmax prediction，即 $\hat{Y}$。

from collections import defaultdict
import numpy as np
from medpy.metric.binary import dc, jc, hd, assd, sensitivity, specificitydef evaluate(Y_pred, Y_true, n_classes):""""medical segmentation evaluationInput:Y_pred, Y_true: [H, W, L], in {0, ..., n_classes - 1}n_classes: intOutput:res: {<metric_name>: [<class_0>, ..., class_nc-1]}"""metric_names = ("dice", "sensitivity", "specificity", "assd", "hd")#, "iou")metric_fn    = (dc, sensitivity, specificity, assd, hd)#, jc)res = defaultdict(list)for c in range(n_classes):B_pred_c = (Y_pred == c).astype(np.uint8)B_c      = (Y_true == c).astype(np.uint8)for metr, fn in zip(metric_names, metric_fn):res[metr].append(fn(B_pred_c, B_c))return res

References

1. 亨氏单位
2. 常用的医学图像分割评价指标
3. 医学图像分割常用指标及代码（pytorch）
4. (MIA 2022) Rethinking adversarial domain adaptation: Orthogonal decomposition for unsupervised domain adaptation in medical image segmentation - paper, github