[NOIP2011 提高组] 选择客栈

题目描述

丽江河边有 $n$ 家很有特色的客栈，客栈按照其位置顺序从 $1$ 到 $n$ 编号。每家客栈都按照某一种色调进行装饰（总共 $k$ 种，用整数 $\sim k-1$ 表示），且每家客栈都设有一家咖啡店，每家咖啡店均有各自的最低消费。

两位游客一起去丽江旅游，他们喜欢相同的色调，又想尝试两个不同的客栈，因此决定分别住在色调相同的两家客栈中。晚上，他们打算选择一家咖啡店喝咖啡，要求咖啡店位于两人住的两家客栈之间（包括他们住的客栈），且咖啡店的最低消费不超过 $p$ 。

他们想知道总共有多少种选择住宿的方案，保证晚上可以找到一家最低消费不超过 $p$ 元的咖啡店小聚。

输入格式

共 $n + 1$ 行。

第一行三个整数 $n, k, p$ ，每两个整数之间用一个空格隔开，分别表示客栈的个数，色调的数目和能接受的最低消费的最高值；

接下来的 $n$ 行，第 $i + 1$ 行两个整数，之间用一个空格隔开，分别表示 $i $ 号客栈的装饰色调 $a_i$ 和 $i$ 号客栈的咖啡店的最低消费 $b_i$ 。

输出格式

一个整数，表示可选的住宿方案的总数。

样例 #1

样例输入 #1

样例输出 #1

提示

样例解释

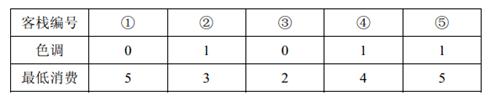
2 人要住同样色调的客栈，所有可选的住宿方案包括：住客栈①③，②④，②⑤，④⑤，但是若选择住 $4, 5$ 号客栈的话， $4, 5$ 号客栈之间的咖啡店的最低消费是 $4$ ，而两人能承受的最低消费是 $3$ 元，所以不满足要求。因此只有前 $3$ 种方案可选。

数据范围

对于 $30% $ 的数据，有 $\leq 100$ ；
对于 $50% $ 的数据，有 $\leq 1\,000$ ；
对于 $100\%$ 的数据，有 $\leq n \leq 2 \times 10^5$ ， $\leq k \leq 50$ ， $\leq p \leq 100$ ， $\leq b_i \leq 100$ 。

暴力代码

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
#define int long long
const int M=1e6;
int read(int &x){scanf("%lld",&x);return x;
}
void print(int x,const char* mw){printf("%lld",x);printf(mw);
}
int n,k,p,a[M],b[M],ans;
signed main(){
// 	freopen("hotel.in","r",stdin);
// 	freopen("hotel.out","w",stdout);read(n);read(k);read(p);for(int i=1;i<=n;i++) read(a[i]),read(b[i]);for (int i=1;i<=n;i++){int minn=b[i];for (int j=i+1;j<=n;j++){minn=min(minn,b[j]);if(a[i]!=a[j]) continue;if (minn<=p) ans++;}}print(ans,"\n");
// 	fclose(stdin);fclose(stdout);return 0;
}

但只能拿60分

思路

由于暴力模拟时间复杂度O( $n^2$ ) 所以过不了，但可以递推,
ch[i]存的是i色调客栈距离前一个能够满足p要求的客栈中间隔了不满足要求的客栈
sum[i]存的是i色调客栈之前的客栈能够满足要求的客栈总数
要求指花费<p
后模拟即可（思路来自题解）

正解代码

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
int ch[55], sum[55], ans, n, k, p;
signed main()
{scanf("%lld%lld%lld", &n, &k, &p);for(int i = 1; i <= n; i++){int color, cost;scanf("%lld%lld", &color, &cost);if(cost <= p){for(int j = 0; j <= 50; j++)if(ch[j]) sum[j]+=ch[j],ch[j] = 0;ans += sum[color], ++sum[color];}else ++ch[color], ans += sum[color];}printf("%lld", ans);return 0;
}