文章目录
- 二、曲面积分
- 2.1 对面积的曲面积分(第一类曲面积分)
- 2.1.1 问题引入 —— 曲面的质量
- 2.1.2 对面积的曲面积分定义及性质
- 2.1.3 对面积的曲面积分的计算法
- 写在最后
二、曲面积分
2.1 对面积的曲面积分(第一类曲面积分)
2.1.1 问题引入 —— 曲面的质量
设 Σ \varSigma Σ 为空间有限光滑或逐片光滑曲面,其面密度为 ρ ( x , y , z ) \rho(x,y,z) ρ(x,y,z) ,求其质量 m m m 。
有两种思想可以进行求解,一是经典积分思想,另一是元素法思想。
(1)经典积分思想
第一步:将 Σ \varSigma Σ 划分为 n n n 个小曲面 Δ S 1 , Δ S 2 , ⋯ , Δ S n \Delta S_1,\Delta S_2,\cdots,\Delta S_n ΔS1,ΔS2,⋯,ΔSn ;
第二步:任取 ( ξ i , η i , δ i ) ∈ Δ S i ( 1 ≤ i ≤ n ) (\xi_i,\eta_i,\delta_i)\in \Delta S_i(1\leq i \leq n) (ξi,ηi,δi)∈ΔSi(1≤i≤n) ,则 m ≈ ∑ ρ ( ξ i , η i , δ i ) Δ S i m \approx \sum\rho(\xi_i,\eta_i,\delta_i)\Delta S_i m≈∑ρ(ξi,ηi,δi)ΔSi ;
第三步:令 λ = max Δ d i ( i = 1 , 2 , ⋯ , n ) \lambda=\max{\Delta d_i}(i=1,2,\cdots,n) λ=maxΔdi(i=1,2,⋯,n) ,其中 d i d_i di 为 Δ S i \Delta S_i ΔSi 的直径,则有 m = lim λ → 0 ∑ i = 1 n ρ ( ξ i , η i , δ i ) Δ S i . m=\lim_{\lambda\to 0}\sum_{i=1}^n\rho(\xi_i,\eta_i,\delta_i)\Delta S_i. m=λ→0limi=1∑nρ(ξi,ηi,δi)ΔSi. (2)元素法思想
第一步,取 d S ⊂ Σ dS\sub \varSigma dS⊂Σ ;第二步, d m = ρ ( x , y , z ) d S dm=\rho(x,y,z) dS dm=ρ(x,y,z)dS ;第三步, m = ∬ Σ ρ ( x , y , z ) d S . m=\iint_{\varSigma}\rho(x,y,z)dS. m=∬Σρ(x,y,z)dS.
2.1.2 对面积的曲面积分定义及性质
由此,我们可以得到对面积的曲面积分的定义:
设 Σ \varSigma Σ 为空间有限曲面,函数 f ( x , y , z ) f(x,y,z) f(x,y,z) 在曲面上有界,将 Σ \varSigma Σ 划分为 n n n 个小曲面 Δ S 1 , Δ S 2 , ⋯ , Δ S n \Delta S_1,\Delta S_2,\cdots,\Delta S_n ΔS1,ΔS2,⋯,ΔSn ;任取 ( ξ i , η i , δ i ) ∈ Δ S i ( 1 ≤ i ≤ n ) (\xi_i,\eta_i,\delta_i)\in \Delta S_i(1\leq i \leq n) (ξi,ηi,δi)∈ΔSi(1≤i≤n) ,作 ∑ ρ ( ξ i , η i , δ i ) Δ S i \sum\rho(\xi_i,\eta_i,\delta_i)\Delta S_i ∑ρ(ξi,ηi,δi)ΔSi ;令 λ = max Δ d i ( i = 1 , 2 , ⋯ , n ) \lambda=\max{\Delta d_i}(i=1,2,\cdots,n) λ=maxΔdi(i=1,2,⋯,n) ,其中 d i d_i di 为 Δ S i \Delta S_i ΔSi 的直径,若极限 lim λ → 0 ∑ i = 1 n ρ ( ξ i , η i , δ i ) Δ S i . \lim_{\lambda\to 0}\sum_{i=1}^n\rho(\xi_i,\eta_i,\delta_i)\Delta S_i. λ→0limi=1∑nρ(ξi,ηi,δi)ΔSi. 存在,称此极限为函数 f ( x , y , z ) f(x,y,z) f(x,y,z) 在曲面 Σ \varSigma Σ 上对面积的曲面积分,记为 ∬ Σ f ( x , y , z ) d S \iint_{\varSigma}f(x,y,z)dS ∬Σf(x,y,z)dS 。
对面积的曲面积分,和二重积分有类似的性质,如常数可以提出来;曲面可以分段;被积函数为 1 时,代表曲面面积;还有就是对称性质,关于 x O y xOy xOy 平面对称,即关于变量 z z z 对称等等。
2.1.3 对面积的曲面积分的计算法
(1)特殊替代法
也就是被积函数可以用曲面方程来替代掉,最终转化为求空间曲面的面积。
回忆一下空间几何里面关于曲面面积的计算方法:两个向量叉乘的一半为所围三角形的面积。
【例】计算 I = ∬ Σ ( 2 x + 4 y / 3 + z ) d S I=\iint_{\varSigma}(2x+4y/3+z)dS I=∬Σ(2x+4y/3+z)dS ,其中 Σ \varSigma Σ 为平面 x / 2 + y / 3 + z / 4 = 1 x/2+y/3+z/4=1 x/2+y/3+z/4=1 在第一卦限的部分。
解: I = 4 ∬ Σ 1 d S = 4 S I=4\iint_{\varSigma}1dS=4S I=4∬Σ1dS=4S 。平面 Σ \varSigma Σ 与三轴的交点分别为 A ( 2 , 0 , 0 ) , B ( 0 , 3 , 0 ) , C ( 0 , 0 , 4 ) A(2,0,0),B(0,3,0),C(0,0,4) A(2,0,0),B(0,3,0),C(0,0,4) ,则 A B → = { − 2 , 3 , 0 } , B C → = { 0 , − 3 , 4 } \overrightarrow{AB}=\{-2,3,0\},\overrightarrow{BC}=\{0,-3,4\} AB={−2,3,0},BC={0,−3,4} ,可计算面积 S = 0.5 × ∣ A B → × B C → ∣ = 61 S=0.5\times|\overrightarrow{AB}\times\overrightarrow{BC}|=\sqrt{61} S=0.5×∣AB×BC∣=61 ,可得 I = 4 61 I=4\sqrt{61} I=461 。
(2)二重积分法
设 Σ : z = u ( x , y ) \varSigma:z=u(x,y) Σ:z=u(x,y) ,其中 ( x , y ) ∈ D (x,y)\in D (x,y)∈D ,则有 d S = 1 + ( ∂ z / ∂ x ) 2 + ( ∂ z / ∂ y ) 2 d x d y dS=\sqrt{1+(\partial z/\partial x)^2+(\partial z/\partial y)^2}dxdy dS=1+(∂z/∂x)2+(∂z/∂y)2dxdy ,有 ∬ Σ f ( x , y , z ) d S = ∬ D [ f ( x , y , u ( x , y ) ] 1 + ( ∂ z / ∂ x ) 2 + ( ∂ z / ∂ y ) 2 d x d y . \iint_{\varSigma}f(x,y,z)dS=\iint_{D}[f(x,y,u(x,y)]\sqrt{1+(\partial z/\partial x)^2+(\partial z/\partial y)^2}dxdy. ∬Σf(x,y,z)dS=∬D[f(x,y,u(x,y)]1+(∂z/∂x)2+(∂z/∂y)2dxdy. 【例】求 I = ∬ Σ z d S I=\iint_{\varSigma}zdS I=∬ΣzdS ,其中 Σ \varSigma Σ 为 x 2 + y 2 + z 2 = 1 x^2+y^2+z^2=1 x2+y2+z2=1 被 z = x 2 + y 2 z=\sqrt{x^2+y^2} z=x2+y2 所截部分。
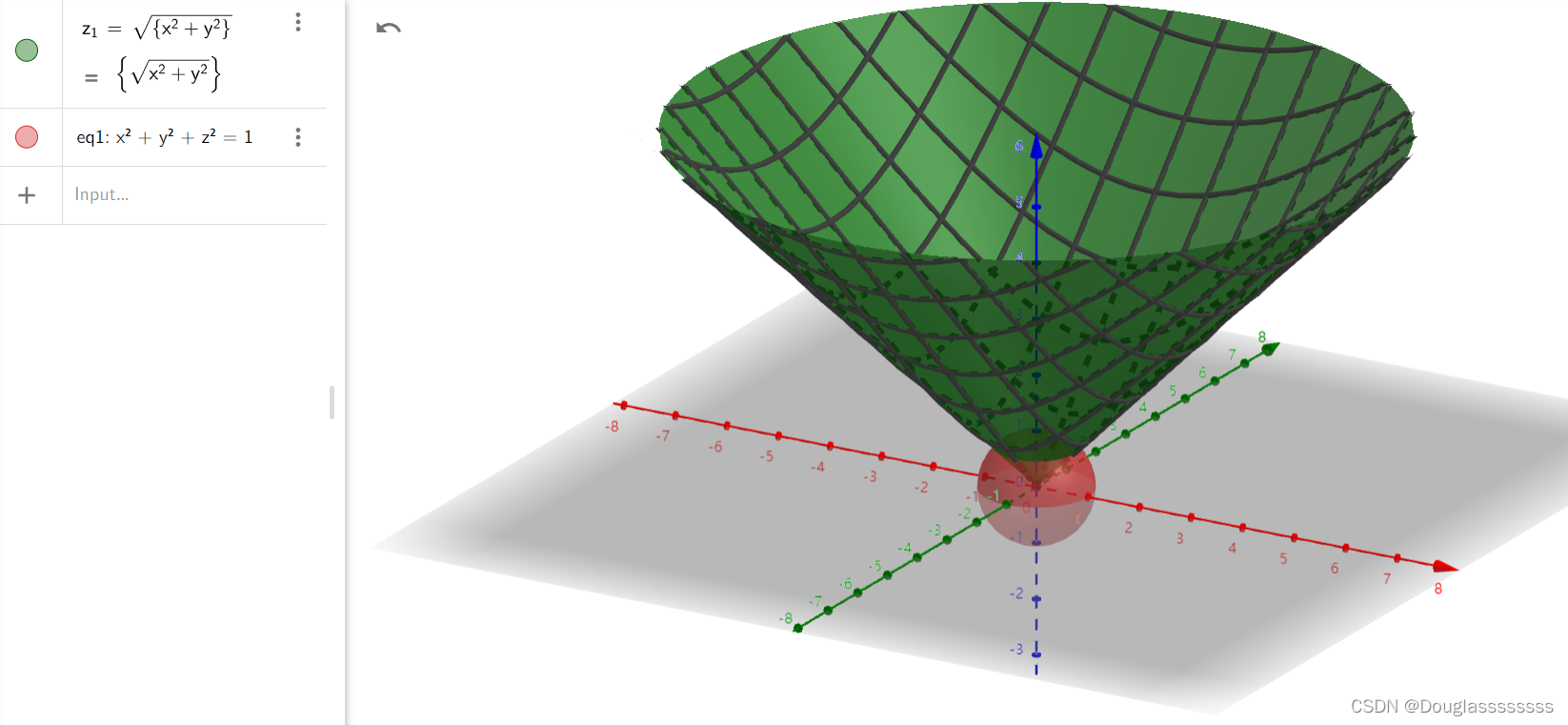
联立两个方程,可得 x 2 + y 2 = 1 / 2 x^2+y^2=1/2 x2+y2=1/2 ,于是有 Σ : z = 1 − x 2 − y 2 , ( x , y ) ∈ D \varSigma:z=\sqrt{1-x^2-y^2},(x,y)\in D Σ:z=1−x2−y2,(x,y)∈D ,其中 D : x 2 + y 2 ≤ 1 / 2. D:x^2+y^2 \leq 1/2. D:x2+y2≤1/2. 则 d S = d S = 1 + ( ∂ z / ∂ x ) 2 + ( ∂ z / ∂ y ) 2 d x d y = 1 / ( 1 − x 2 − y 2 ) d x d y dS=dS=\sqrt{1+(\partial z/\partial x)^2+(\partial z/\partial y)^2}dxdy=1/(\sqrt{1-x^2-y^2})dxdy dS=dS=1+(∂z/∂x)2+(∂z/∂y)2dxdy=1/(1−x2−y2)dxdy ,于是 I = ∬ D 1 − x 2 − y 2 ⋅ ( 1 / 1 − x 2 − y 2 ) d x d y = S D = π / 2. I=\iint_{D}\sqrt{1-x^2-y^2}\cdot(1/\sqrt{1-x^2-y^2})dxdy=S_D=\pi/2. I=∬D1−x2−y2⋅(1/1−x2−y2)dxdy=SD=π/2.
写在最后
第一类曲面积分和第一类曲线积分很是相似,都是化成对应的简单面积分或线积分来进行计算,如果掌握了二重积分,加上空间几何的内容,相信这一部分是可以较为轻松掌握的。