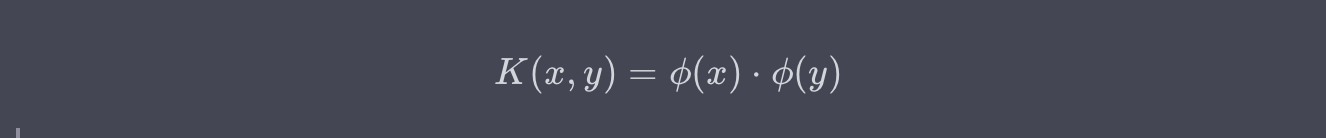Appium 全新 2.0 全新跨平台生态，版本特性抢鲜体验！

关于Appium V2

Appium V2 beta版本在2021年发布，从2022年1月1号开始，Appium核心团队不会再维护Appium 1.x版本了，所有近期官方发布的平台驱动（如Android平台的UIAutomator，IOS平台的XCUITest）不再兼容Appium 1.x，需要基于Appium V2版本。

让我们一起看看Appium V2相比Appium 1.x发生了哪些变化

关于Appium V2的变化
将平台驱动独立了出来
·在Appium V2版本中驱动和Appium Server是分开的，驱动可以分开安装和升级，比如Android平台的UIAutomator、IOS平台的XCUITest等

引入插件生态
Appium V2中将一些非核心部分组件功能转移到了插件中，并且能够通过插件的模式能够扩展更多的新功能，比如通过官方的images插件可以使用图像识别来定位元素，使用第三方插件appium-device-farm能够集中管理设备

严格遵循W3C协议
类似于Selenium 4中引入的W3C协议，Appium V2中严格遵循W3C协议。在Appium V2编写测试脚本时填写capabilities需要指定appium:前缀，比如：

{    "platformName": "Android","appium:automationName": "uiautomator2","appium:deviceName": "emulator-5554","appium:appPackage": "com.lemon.lemonban","appium:appActivity": "com.lemon.lemonban.activity.WelcomeActivity"
}

具体哪些属于标准W3C协议中的capabilities可以查看文档https://www.w3.org/TR/webdriver/#capabilities

其中platformName是属于标准的W3C协议中的capabilities，不需要添加前缀

非标准的W3C协议中的capabilities需要添加appium:前缀

使用前准备工作:
Appium V2版本目前需要基于nodejs环境进行安装，并且对nodejs的版本也有对应的要求：

Node.js version in the SemVer range ^14.17.0 || ^16.13.0 || >=18.0.0

NPM version >= 8 (NPM is usually bundled with Node.js, but can be upgraded independently)

这里我们选择直接从nodejs的官网https://nodejs.org/en下载最新的版本：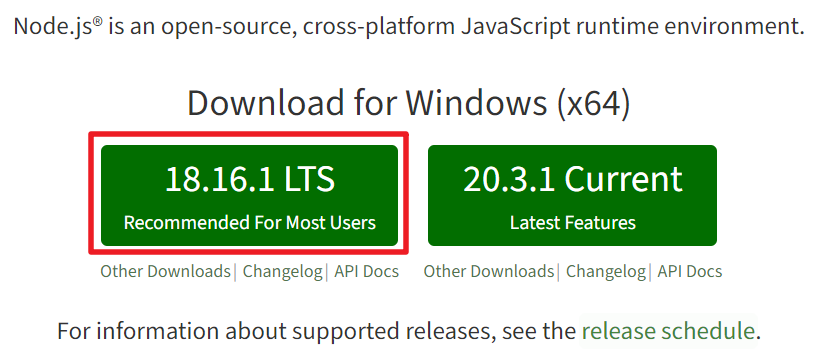

Step1：安装Appium V2

npm install -g appium@next

目前Appium V2还未最终正式发布，还属于rc（Release Candidate-发布候选版）版本，在安装时必须要使用appium@next参数进行安装。当Appium V2正式发布之后我们可以使用appium参数来安装。

安装完毕之后检测appium版本号：

appium -v

输出结果为：

2.0.0-rc.3

当Appium V2安装好之后，即可通过Appium Extension CLI（Appium扩展命令行）模式来扩展安装各种平台驱动和插件了。

Step2：安装Appium driver

以Android平台为例，安装UIAutomator2驱动：

appium driver install uiautomator2  //Appium扩展命令行模式

安装完毕之后可以查看安装好的驱动：

appium driver list

输出结果为：

Step3：启动Appium Server

使用appium命令即可启动：

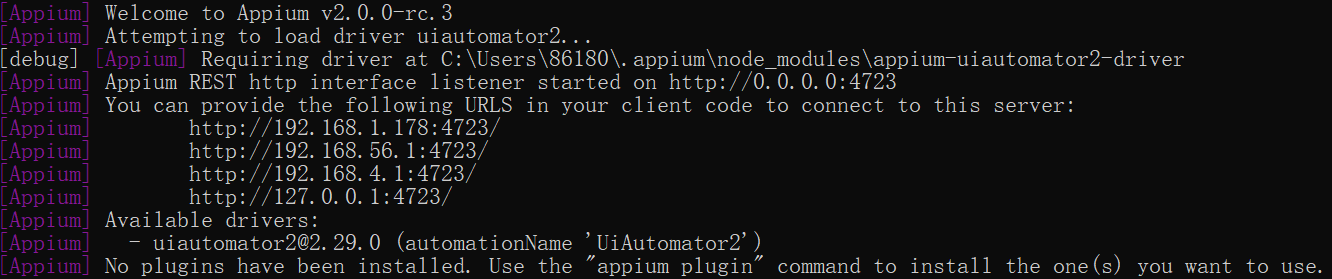
appium默认会以4723端口启动，并且在启动的时候会在本地加载已安装好的驱动。

Step4：安装Appium客户端库
选择编程语言的对应的Appium客户端库，如Python对应的是Appium-Python-Client，通过pip进行安装；Java对应的是Java-client，通过Maven或者Gradle进行安装。

这里需要注意，如果之前的项目用到了相关的库，需要将其进行升级以适配最新的Appium V2。

Step5：编写测试脚本

这里以python为例：

from appium import webdrivercaps = {"platformName": "Android","automationName": "uiautomator2","deviceName": 'emulator-5554',"appPackage": "com.lemon.lemonban","appActivity": "com.lemon.lemonban.activity.WelcomeActivity","noReset": True
}
appium_server_url = 'http://127.0.0.1:4723'
driver = webdriver.Remote(appium_server_url, caps)

需要注意的是：Appium Server在1.x版本时期的访问地址是：http://127.0.0.1/wd/hub, 但是在V2版本上不需要后缀/wd/hub了，如果还用之前的地址访问会出现404。

最后感谢每一个认真阅读我文章的人，礼尚往来总是要有的，虽然不是什么很值钱的东西，如果你用得到的话可以直接拿走：