读书笔记｜《数据压缩入门》—— 柯尔特·麦克安利斯亚历克斯·海奇

前言：在接触文本隐写研究领域时了解到这本书。本书可算作《数据压缩》的入门书籍之一，这本书对熵编码、变长编码、统计编码、自适应统计编码、字典编码、上下文编码等常用编码方式的定义及来源进行介绍，对不同场景下不同格式的压缩数据有针对性地分析，笔风幽默，强烈推荐！本书中共有15个章节，本人主要阅读了前9个章节，以下是阅读本书过程中的一些笔记，供大家参考。

◆ 序

无损方法
• 去掉重复数据（LZ算法）
• 熵压缩（哈夫曼编码、算术编码）

有损方法
• 降低精度（截断或降采样）
• 图像 / 视频压缩
• 音频压缩

◆ 第1章并非无趣的一章

数据压缩无非是用最紧凑的方式来表示数据。
数据压缩算法有5类：变长编码(variable-length codes，VLC）、统计压缩（statistical compression）、字典编码（dictionary encodings）、上下文模型（context modeling）和多上下文模型（multicontext modeling）。所有这5类算法都有很多变种。
1948年，香农又发表了《通信的数学理论》，在这篇论文中他详细论述了发送者怎样对要发送的信息进行编码才能达到最佳效果，由此开创了信息论（information theory）这一全新的学术领域。对消息进行编码有多种方式，“字母表”与“摩尔斯码”只是其中常见的两种。但是对每一个特定的消息来说，都有一个最佳的编码方式，这里的“最佳”指的是传递消息时用到的字母或者符号（也可以说是二进制位，即信息的单位）最少。至于这里说的“最少”到底是多少，则取决于消息所包含的信息内容。香农发明了一种度量消息所携带信息内容的方法，并称之为信息熵（information entropy）。数据压缩其实是香农的研究工作的一项实际应用，它所研究的问题是，“在保证信息能恢复的前提下，我们能将消息变得多么紧凑”。
对数据进行压缩，通常有两个思路：
- 减少数据中不同符号的数量（即让“字母表”尽可能小）；
- 用更少的位数对更常见的符号进行编码（即最常见的“字母”所用的位数最少）。

60年来的数据压缩研究都可以归结到上面两个重要思路上，数据压缩中的每一个算法都聚焦于解决这两件事情中的一件。每一个压缩算法，要么通过打乱符号或减少符号的数量，将数据转换得更便于压缩；要么利用其中一些符号比其他符号更常见的事实，通过用最少的位数编码最常见的符号，实现压缩的目的。

虽然数据压缩的思路简单明了，但在实际应用中数据压缩很复杂。其原因在于，由于要压缩的数据的类型不同，针对上述两条思路中的每一条，能采用的方法都有很多。因此，进行实际的数据压缩时，需要综合考虑以下因素。
- 不同数据的处理方法不同，比如压缩一本书中的文字和压缩浮点型的数，其对应的算法就大不相同。
- 有些数据必须经过转换才能变得更容易压缩。
- 数据可能是偏态的。例如，夏天的整体气温偏高，也就是说高气温出现的频率比接近零度的气温出现的频率高很多。
互联网诞生的那一年，也就是1978年。
在很长一段时间内，莱娜图是用来测试图像压缩算法的标准测试图。幸运的是，从此以后，很少再出现这样有争议性的图像语料库。（我们两位作者则更喜欢使用柯达公司的图像测试集。）然而即使是今天，仍然有很多图像压缩方面的论文将莱娜图用作检验算法的标准。

◆ 第2章不容错过的一章

数据压缩所做的无非就是尽可能减少表示特定数据集时所需的二进制位数量。
根据信息论的观点，一个数值所包含的信息内容等于，为了在一个集合中唯一地确定这个数值，需要做出的二选一（是/否）决定的次数。
给定任意一个整数，我们都能将它转换为二进制形式。然而令人遗憾的是，给定一个整数，如果不经过二进制转换这一过程，我们很难直接知道它需要占几个二进制位。转换过程很无趣，但好在数学家已准备了下面的公式，让我们可以更轻松地处理这个问题：
$L OG 2 (x) = ce i l (l o g (x + 1) / l o g (2))$ : 表示一个数所需要的二进制位数

在这里插入图片描述

给定任意一个十进制整数，通过计算它对应的LOG2函数的值，我们就能知道用二进制来表示这个数最少需要多少二进制位。香农将一个变量对应的LOG2函数的值定义为它的熵（entropy），也就是用二进制来表示这个数所需的最少二进制位数。
数值的LOG2表示形式虽然高效，但对于制造计算机元件的方式来说并不实用。这其中的问题在于，如果用最少的二进制位数来表示一个数，在解码相应的二进制字符串时会产生混乱（因为我们并不知道该数对应的LOG2长度），会与硬件的执行性能相冲突，两者不能兼顾。现代计算机采用了折中的方案，用固定长度的二进制位数来表示大小不同的整数。最基本的存储单元是一个字节，由8个二进制位组成。在现代编程语言中，通常可用的整数的存储类型包括：短整型16个二进制位、整型32个二进制位、长整型64个二进制位。因此，对于十进制数10，虽然其对应的二进制数为1010，但在实际存储中是短整型，在计算机中的实际表示为0000000000001010。显然，这样做浪费了很多的二进制位。

◆ 第3章突破熵

香农博士将一个数对应的LOG2函数值称为该数的熵，也就是表示这个数所需要的最少二进制位数。他进一步将熵的概念（既然已经提出了这一术语了，为什么不重复利用呢……）扩展到整个数据集，也就是表示整个数据集所需要的最少二进制位数。他完成了所有这方面的数学工作，并给出了下面这个优美的公式来计算一个集合的熵： $-\sum_{i=1}^{n}{p_{i}} · {lb(p_{i})}, lb(p_{i}) = log(p_{i})/log(2))$

在这里插入图片描述

https://rosettacode.org/wiki/Entropy 熵的各种语言实现。
为了使表示某个数据集所需的二进制位数最少，数据集中的每个符号平均所需的最小二进制位数就是熵。
从本质上来说，香农所定义的熵，是以一种倒排序的方式建立在数据流中每个符号出现概率的估算之上的。
总的来说，一个符号出现得越频繁，它对整个数据集包含的信息内容的贡献就会越少，这看起来似乎完全违背直觉。
数据集中包含的总体信息很少，因此对应的熵值也很小。
突破熵的关键在于，通过利用数据集的结构信息将其转换为一种新的表示形式，而这种新表示形式的熵比源信息的熵小。
需要记住的是，熵定义的只是在对数据流进行编码时，每个符号平均所需的最小二进制位数。这就意味着，有些符号需要的二进制位数比熵小，而有些符号需要的二进制位数则比熵大。
柯尔莫哥洛夫复杂性（Kolmogorov complexity），度量的是确定一个对象所需要的计算资源。

◆ 第4章 VLC

摩尔斯码根据各个符号在英语中出现的概率来为其分配点和划。一个符号出现得越频繁，其对应的编码就越短。即使是追溯到19世纪，这也是对符号分配变长编码（variable-length codes，VLC）的最初实现之一，其目的则在于减少传输信息过程中所需要的总工作量。
为了进行数据压缩，我们的目的很简单：给定一个数据集中的符号，将最短的编码分配给最可能出现的符号。
设计VLC集的码字时，必须考虑两个原则：一是越频繁出现的符号，其对应的码字越短；二是码字需满足前缀性质。

◆ 第5章统计编码

统计编码算法通过数据集中符号出现的概率来进行编码使结果尽可能与熵接近。
哈夫曼编码：
算术编码：
主流的统计编码方法有哈夫曼编码和算术编码，但ANS（非对称数字系统编码）改变了一切。虽然它在数据压缩领域里出现的时间还不长，但是已开始取代过去20多年里占据主流地位的哈夫曼编码和算术编码。例如，ZHuff、LZTurbo、LZA、Oodle和LZNA这些压缩工具已开始使用ANS。鉴于其速度和性能，ANS成为主要的编码方法似乎只是时间问题。实际上，在2013年，这一算法又出现了一个被称为有限状态熵（Finite State Entropy，FSE）的更注重性能的版本，它只使用加法、掩码和移位运算，使ANS对开发人员更具吸引力。它的性能是如此强大，以至于2015年推出了一款名为LZFSE的GZIP变种，作为苹果下一代iOS版本的核心API。

◆ 第6章自适应统计编码

数据中总会存在某种类型的局部偏态（locality-dependent skewing），将某些符号、想法或者单词集中在数据集的某个子区间里。

◆ 第7章字典编码

虽然信息论的创立是在20世纪40年代，哈夫曼编码的提出是在20世纪50年代，而互联网的出现在20世纪70年代，但是直到20世纪80年代，数据压缩才真正引起了人们的兴趣。随着互联网的快速发展，人们分享的内容已不再局限于文字，而是开始分享比文本大得多的照片以及其他格式的数据。同时这种分享又发生在网络带宽有限、存储昂贵的时期，数据压缩因此成了缓解这些瓶颈的关键。虽然VLC一直都在发挥作用，但它与熵绑定的事实也限制了数据压缩未来的发展。因此，当大多数研究人员在尝试寻找更有效的VLC技术时，也有少数研究人员选择了不同的路，他们找到了使统计压缩可以更有效地预处理数据的新方法。这种新方法通常被称为“字典转换”（dictionary transforms），它完全改变了人们对数据压缩的认知。突然间，压缩变成了一种对各种类型的数据都有用的算法。它的应用范围非常广泛，事实上今天所有的主流压缩算法（比如GZIP或者7-Zip）都会在核心转换步骤中使用字典转换。

在这里插入图片描述

字典编码的关键是要找到那些能生成最小熵的词。1977年，两位研究人员Abraham Lempel和Jacob Ziv提出了几种解决“理想分词”问题的方法。这些算法根据提出的年份分别被命名为LZ77 和LZ78，它们在找出最佳分词方面非常高效，30多年来还没有其他算法可以取代它们。

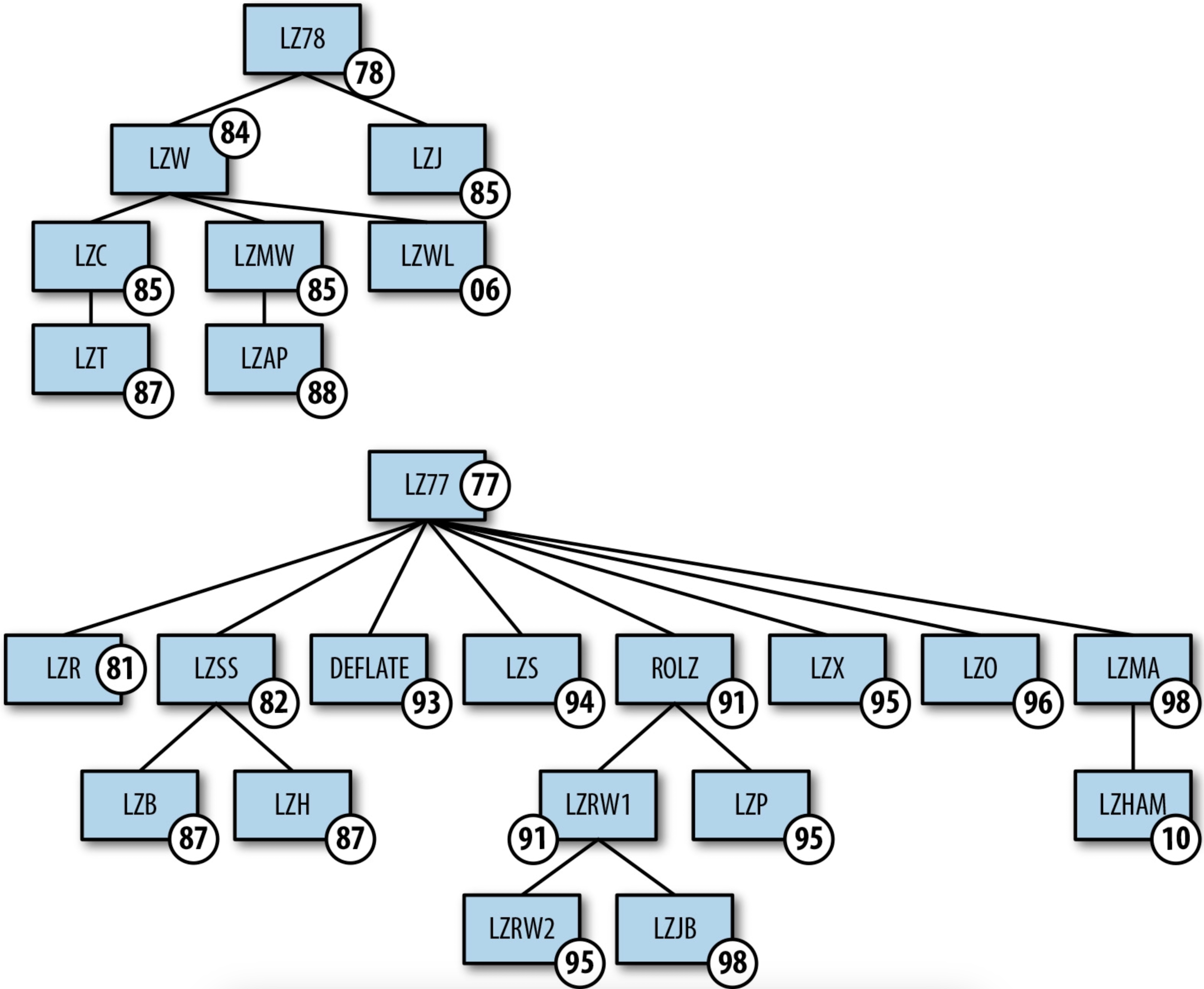
◆ 第8章上下文数据转换

给定一组相邻的符号集，对它们进行某种方式的变换使其更容易压缩。我们通常称这样的变换为“上下文变换”（contextual transform），因为在思考数据的理想编码方式时，这些方法考虑到了邻近符号的影响。
这些变换的目标是一致的，即通过对这些信息进行某种方式的变换，使统计编码算法对其进行压缩时更高效。
变换数据的方法有很多种，但其中有3种对现代的数据压缩来说最为重要，即行程编码(run-length encoding，RLE）、增量编码（delta coding）和伯罗斯–惠勒变换（Burrows-Wheeler transform，BWT）。
增量编码的目的就是缩小数据集的变化范围。更确切地说，是为了减少表示数据集中的每个值所需要的二进制位数。