【算法学习】-【双指针】-【快乐数】

LeetCode原题链接：202. 快乐数

下面是题目描述：

「快乐数」定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。
如果这个过程结果为 1，那么这个数就是快乐数。
如果 n 是快乐数就返回 true ；不是，则返回 false 。

示例 1：
输入：n = 19
输出：true
解释：
1² + 9² = 82
8² + 2² = 68
6² + 8² = 100
1² + 0² + 0² = 1

示例 2：
输入：n = 2
输出：false

提示：
1 <= n <= 2³¹ - 1

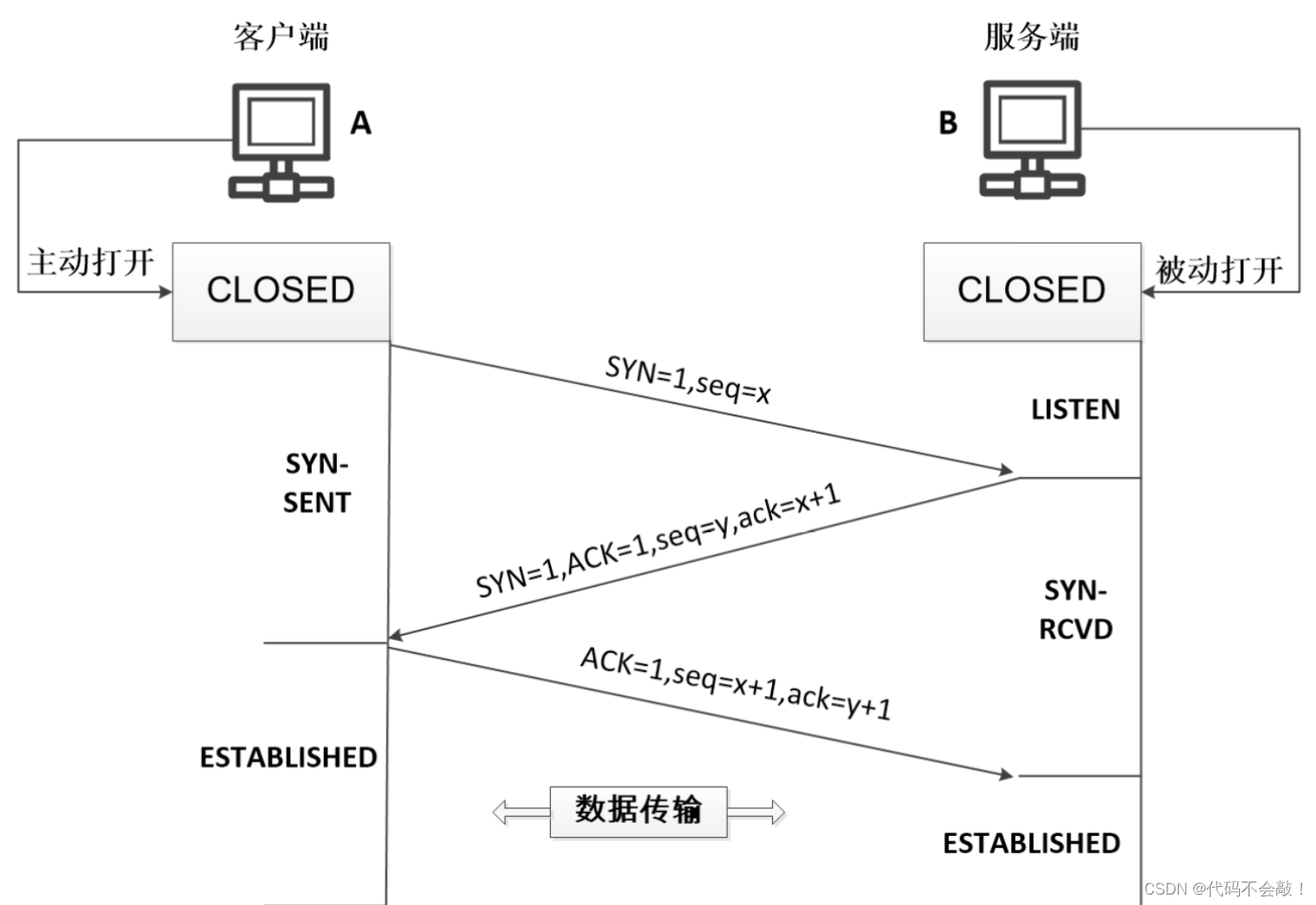
1、题目分析
根据题目说明，给定的一个正整数，每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程，直到这个数变为 1，也可能是无限循环但始终变不到1；对于始终变不到1的情况，有没有可能不是循环但仍一直在变化呢？

答案是不可能。运用鸽巢原理可以证明这一点。那么下面是简单的证明过程：
先简单地说明一下鸽巢原理，也就抽屉原理，指的是：有n个鸽巢，n+1个鸽子，鸽子全部往巢中飞时，至少有一个鸽巢中鸽子的数量是大于1的
接下来开始证明。由题目所给的数据范围，我们可通过最大的一个数可以计算得到“鸽巢”的大小（范围）， 2³¹ - 1 = 2,147,483,647 ，经题目要求的计算方式计算一次可以得到一个数，260。那么任意一个符合题目数据范围的数只会在[1, 260]这个区间内变化，这个区间也就是“鸽巢”。也就是说，只要一个正整数比 2³¹ - 1 小，它的变化只会在[1, 260]中，极端来看，一个数在变化了260次之后（把n个鸽巢填满），下一次变化也绝对会在这个范围中（让某个鸽巢中鸽子的数量大于1），因为那个数不管变成多少都一定比2³¹ - 1 小。由此我们就无需担心一开始的那个问题。

2、解题思路
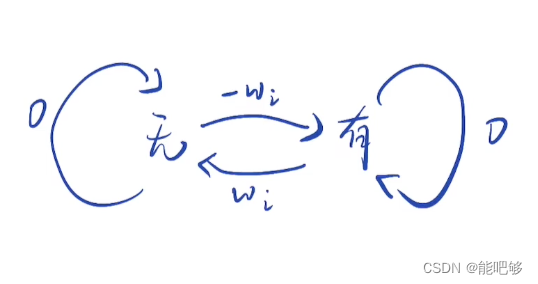
根据上面分析，给定的正整数要么是无限循环，要么最后变成1；再通过对两个示例中算出来的数进行 “连接”，会发现这个问题可以转换成为链表带环问题。如下图：
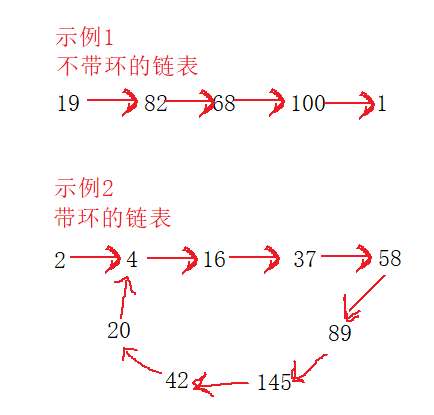
在这里插入图片描述
所以可以直接按解决链表带环的问题方法解决本题。唯一需要变化的就是快慢指针的定义。链表带环问题中，快指针一次走两步，慢指针一次走一步；在本题中，快指针一次按要求计算两次，慢指针按要求计算一次，最后判断两个指针是否相遇即可。

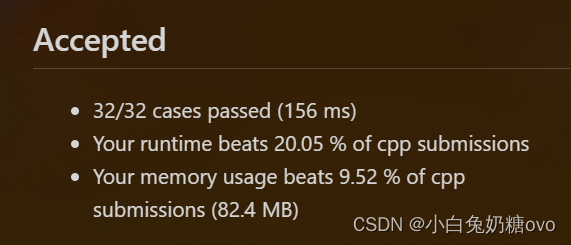
3、具体代码

class Solution {
public:int calculate(int num){int sum = 0;while(num){sum += pow(num % 10, 2);num /= 10;}return sum;}bool isHappy(int n) {int slow = calculate(n);int fast = calculate(calculate(n));while(slow != 1 && fast != 1){if(slow == fast){return false;}slow = calculate(slow);     //slow++;fast = calculate(calculate(fast));   //fast+=2;}return true;}
};