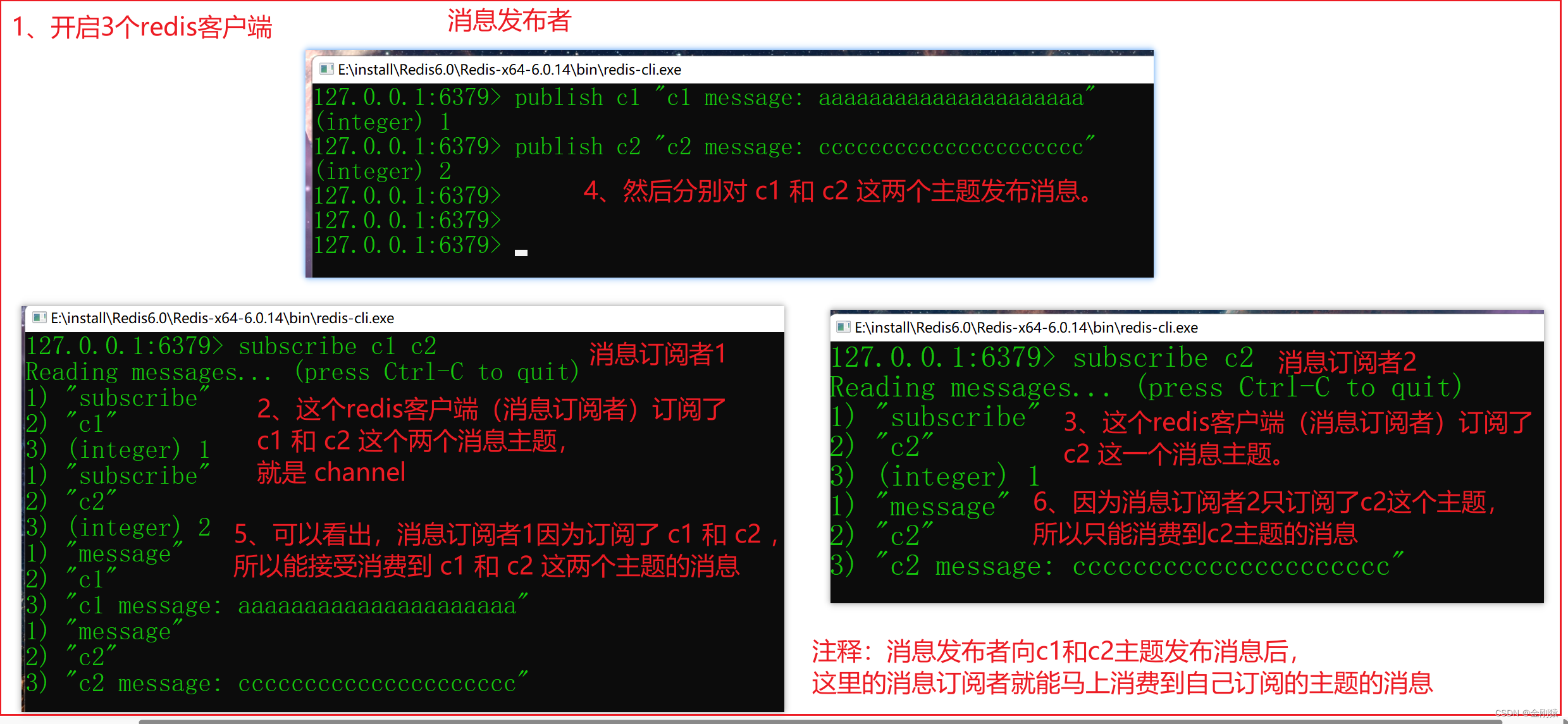
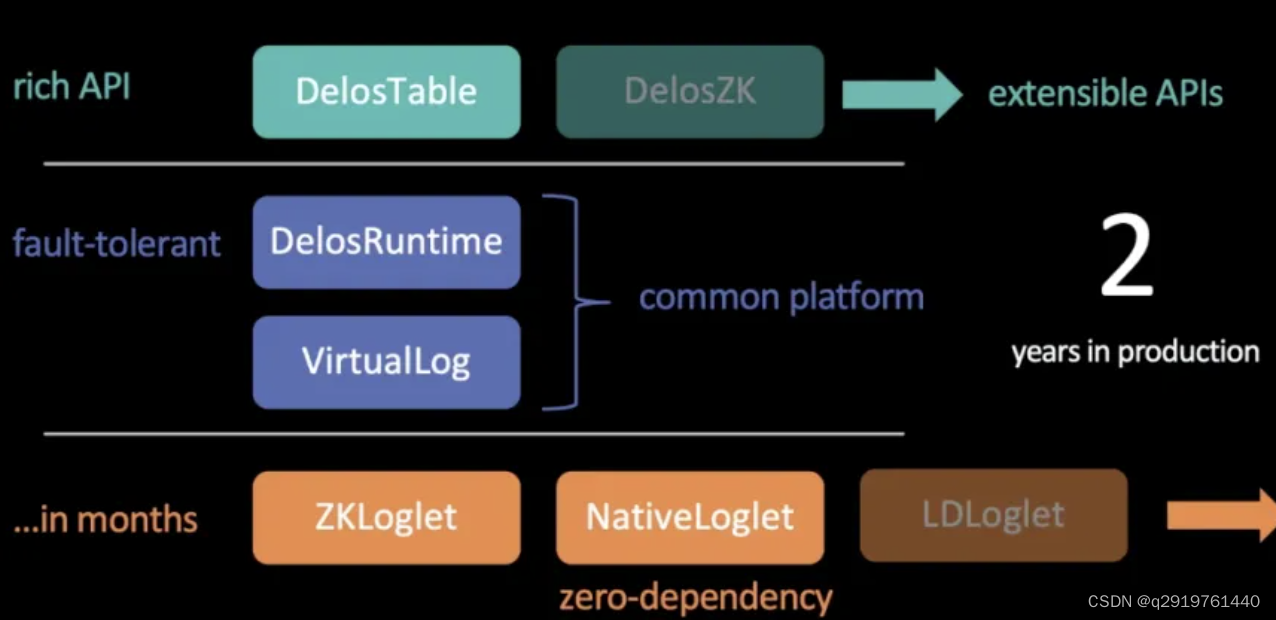
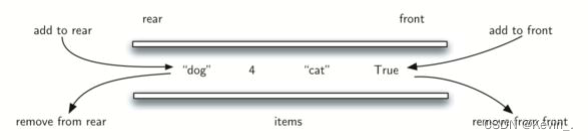
一、理论基础

1、CAP定理

1998年，加州大学的计算机科学家 Eric Brewer 提出，分布式系统有三个指标：

Eric Brewer 说，分布式系统无法同时满足这三个指标。

这个结论就叫做 CAP 定理。

CAP定理- Consistency

Consistency（一致性）：用户访问分布式系统中的任意节点，得到的数据必须一致

CAP定理- Availability

Availability （可用性）：用户访问集群中的任意健康节点，必须能得到响应，而不是超时或拒绝

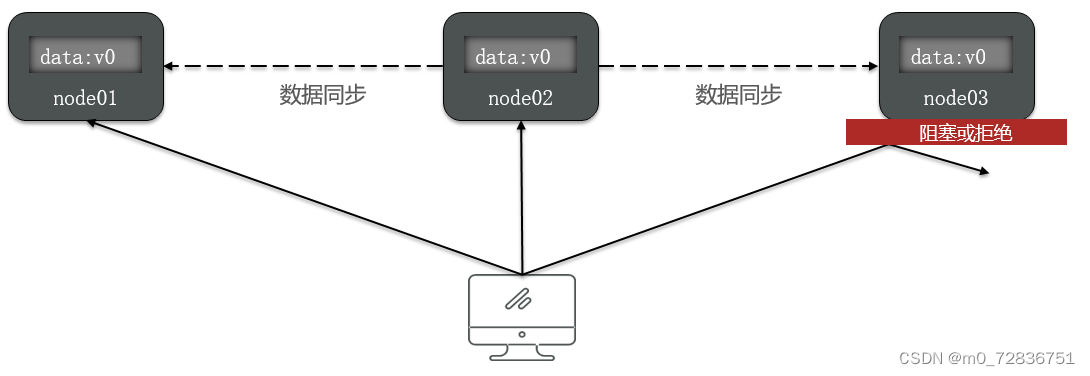
CAP定理-Partition tolerance

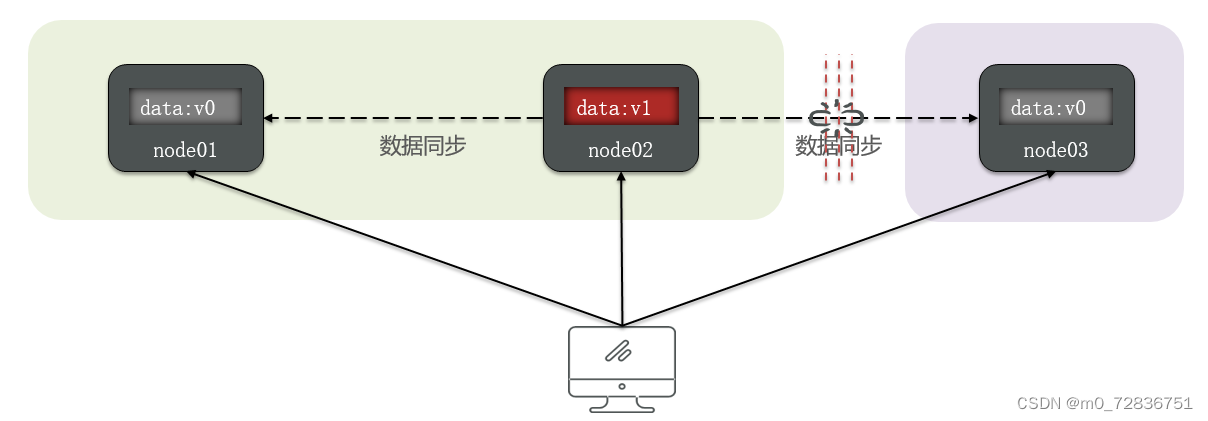
Partition（分区）：因为网络故障或其它原因导致分布式系统中的部分节点与其它节点失去连接，形成独立分区。

Tolerance（容错）：在集群出现分区时，整个系统也要持续对外提供服务

总结：

简述CAP定理内容？

思考：elasticsearch集群是CP还是AP？

2、BASE理论

BASE理论是对CAP的一种解决思路，包含三个思想：

而分布式事务最大的问题是各个子事务的一致性问题，因此可以借鉴CAP定理和BASE理论：

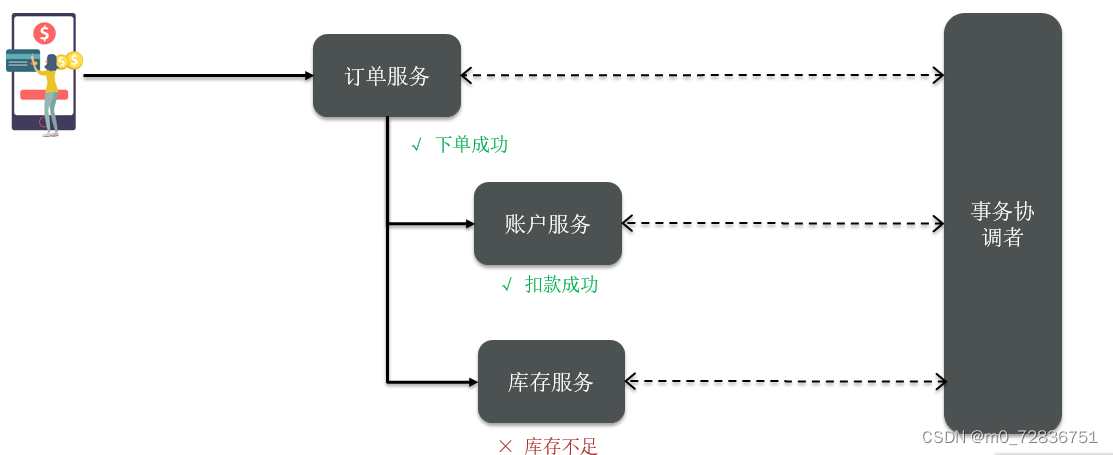
分布式事务模型

解决分布式事务，各个子系统之间必须能感知到彼此的事务状态，才能保证状态一致，因此需要一个事务协调者来协调每一个事务的参与者（子系统事务）。

这里的子系统事务，称为分支事务；有关联的各个分支事务在一起称为全局事务

总结：

简述BASE理论三个思想：

解决分布式事务的思想和模型：

二、初识Seata

1、Seata的架构

Seata是 2019 年 1 月份蚂蚁金服和阿里巴巴共同开源的分布式事务解决方案。致力于提供高性能和简单易用的分布式事务服务，为用户打造一站式的分布式解决方案。

官网地址：Seata | Seata，其中的文档、播客中提供了大量的使用说明、源码分析。

Seata架构

Seata事务管理中有三个重要的角色：

•TC (Transaction Coordinator) - 事务协调者：维护全局和分支事务的状态，协调全局事务提交或回滚。

•TM (Transaction Manager) - 事务管理器：定义全局事务的范围、开始全局事务、提交或回滚全局事务。

•RM (Resource Manager) - 资源管理器：管理分支事务处理的资源，与TC交谈以注册分支事务和报告分支事务的状态，并驱动分支事务提交或回滚。

初识Seata

Seata提供了四种不同的分布式事务解决方案：

2、部署TC服务

3、微服务集成Seata

1.首先，引入seata相关依赖：

2.然后，配置application.yml，让微服务通过注册中心找到seata-tc-server：

总结：

nacos服务名称组成包括？

seata客户端获取tc的cluster名称方式？

三、动手实践

1、XA模式

XA模式原理

XA 规范 是 X/Open 组织定义的分布式事务处理（DTP，Distributed Transaction Processing）标准，XA 规范 描述了全局的TM与局部的RM之间的接口，几乎所有主流的数据库都对 XA 规范 提供了支持。

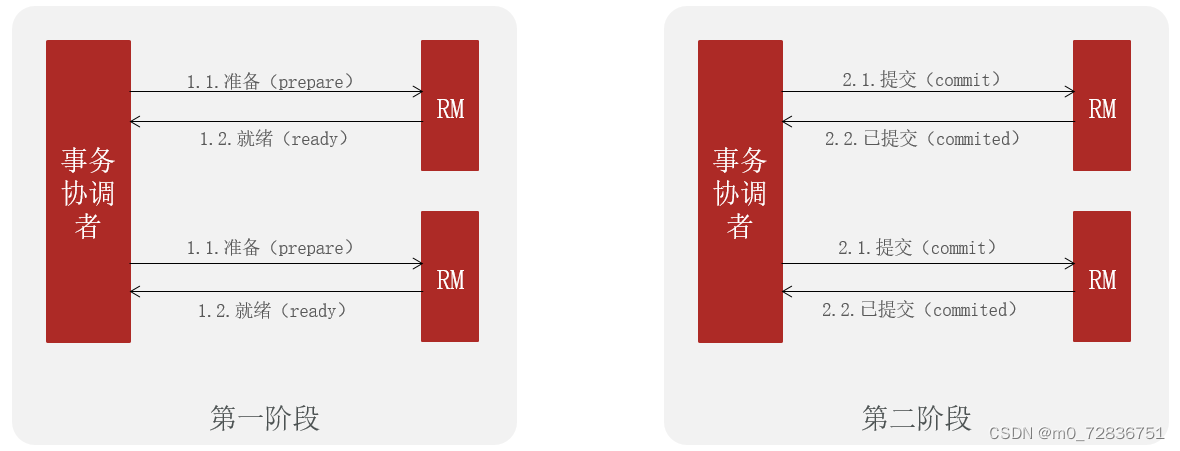
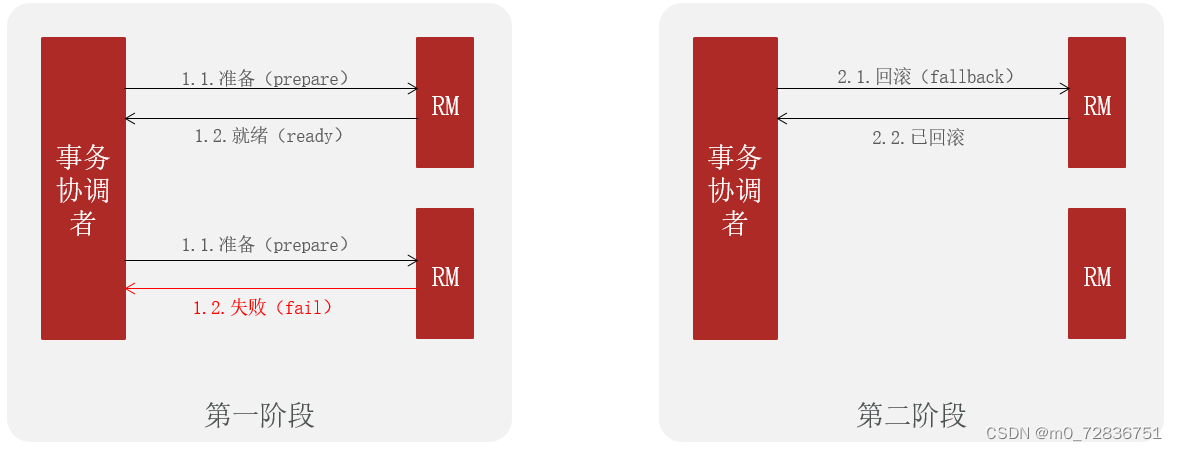
seata的XA模式

seata的XA模式做了一些调整，但大体相似：

RM一阶段的工作：

TC二阶段的工作：

RM二阶段的工作：

总结：

XA模式的优点是什么？

XA模式的缺点是什么？

实现XA模式

Seata的starter已经完成了XA模式的自动装配，实现非常简单，步骤如下：

1.修改application.yml文件（每个参与事务的微服务），开启XA模式：

2.给发起全局事务的入口方法添加@GlobalTransactional注解，本例中是OrderServiceImpl中的create方法：

3.重启服务并测试

2、AT模式

AT模式原理

AT模式同样是分阶段提交的事务模型，不过缺弥补了XA模型中资源锁定周期过长的缺陷。

阶段一RM的工作：

阶段二提交时RM的工作：

阶段二回滚时RM的工作：

总结：

简述AT模式与XA模式最大的区别是什么？

AT模式的优点：

AT模式的缺点：

实现AT模式

AT模式中的快照生成、回滚等动作都是由框架自动完成，没有任何代码侵入，因此实现非常简单。

1.导入Sql文件：seata-at.sql，其中lock_table导入到TC服务关联的数据库，undo_log表导入到微服务关联的数据库：

2.修改application.yml文件，将事务模式修改为AT模式即可：

3.重启服务并测试

3、TCC模式

TCC模式原理

TCC模式与AT模式非常相似，每阶段都是独立事务，不同的是TCC通过人工编码来实现数据恢复。需要实现三个方法：

举例，一个扣减用户余额的业务。假设账户A原来余额是100，需要余额扣减30元。

TCC的工作模型图：

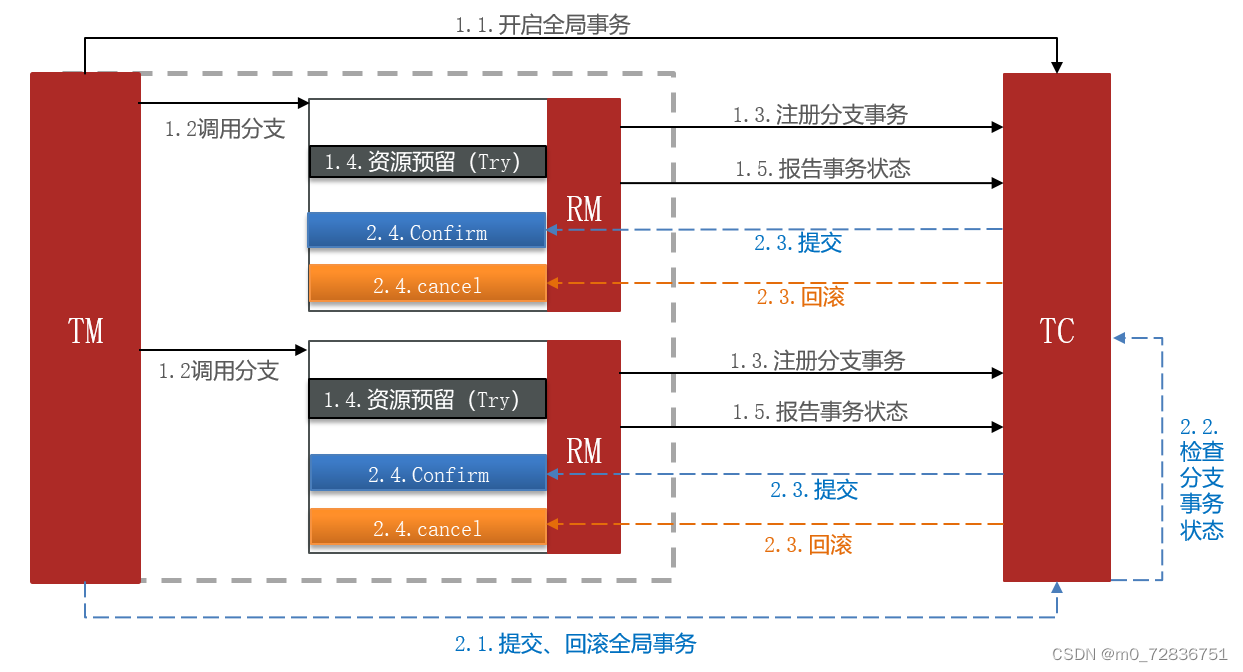
总结：

TCC模式的每个阶段是做什么的？

TCC的优点是什么？

TCC的缺点是什么？

TCC的空回滚和业务悬挂

当某分支事务的try阶段阻塞时，可能导致全局事务超时而触发二阶段的cancel操作。在未执行try操作时先执行了cancel操作，这时cancel不能做回滚，就是空回滚。

对于已经空回滚的业务，如果以后继续执行try，就永远不可能confirm或cancel，这就是业务悬挂。应当阻止执行空回滚后的try操作，避免悬挂

业务分析

声明TCC接口

TCC的Try、Confirm、Cancel方法都需要在接口中基于注解来声明，语法如下：

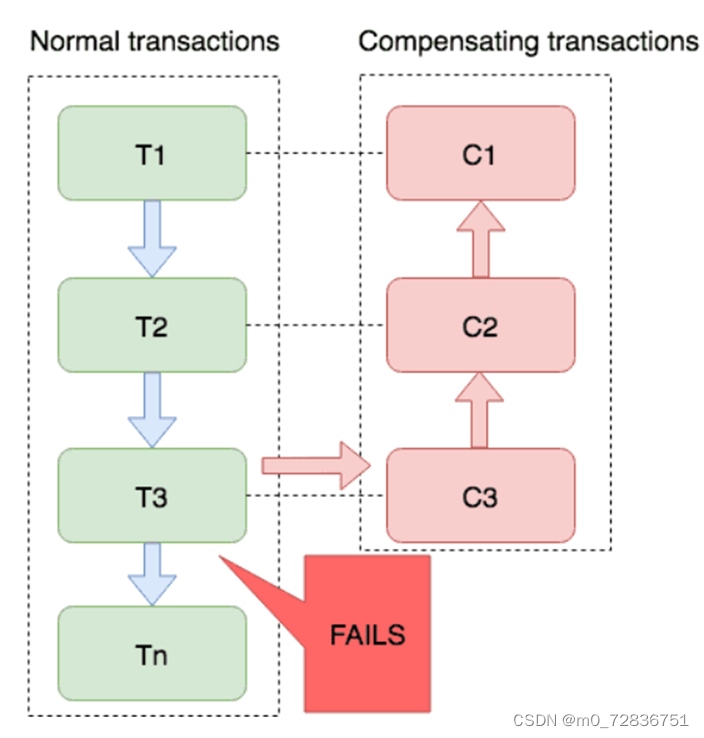
4、SAGA模式

Saga模式是SEATA提供的长事务解决方案。也分为两个阶段：

Saga模式优点：

缺点：

四种模式对比

	XA	AT	TCC	SAGA
一致性	强一致	弱一致	弱一致	最终一致
隔离性	完全隔离	基于全局锁隔离	基于资源预留隔离	无隔离
代码侵入	无	无	有，要编写三个接口	有，要编写状态机和补偿业务
性能	差	好	非常好	非常好
场景	对一致性、隔离性有高要求的业务	基于关系型数据库的大多数分布式事务场景都可以	• 对性能要求较高的事务。 • 有非关系型数据库要参与的事务。	• 业务流程长、业务流程多 • 参与者包含其它公司或遗留系统服务，无法提供 TCC 模式要求的三个接口

四、高可用

TC的异地多机房容灾架构

TC服务作为Seata的核心服务，一定要保证高可用和异地容灾。