怒刷LeetCode的第23天（Java版）

第一题

题目来源

题目内容

解决方法

方法一：贪心算法

方法二：动态规划

方法三：回溯算法

方法四：并查集

第二题

题目来源

题目内容

解决方法

方法一：排序和遍历

方法二：扫描线算法

方法三：栈

第三题

题目来源

题目内容

解决方法

方法一：遍历和比较

第一题

题目来源

55. 跳跃游戏 - 力扣（LeetCode）

题目内容

解决方法

方法一：贪心算法

这个算法使用贪心的思想，通过遍历数组中的每个元素，始终保持一个能够跳到的最远位置 maxPos。在遍历过程中，如果当前位置超过了 maxPos，则说明无法继续跳跃，返回 false。否则，更新 maxPos 的值，将其与 i + nums[i] 比较，取较大值作为新的 maxPos。最后判断 maxPos 是否已经超过或等于最后一个下标，如果是，则返回 true，否则返回 false。

class Solution {
public boolean canJump(int[] nums) {int n = nums.length;int maxPos = 0; // 当前能够跳到的最远位置for (int i = 0; i < n; i++) {if (i > maxPos) {// 如果当前位置超过了能够跳到的最远位置，说明无法继续跳跃，返回falsereturn false;}maxPos = Math.max(maxPos, i + nums[i]);// 更新能够跳到的最远位置if (maxPos >= n - 1) {// 如果能够跳到的最远位置已经超过或等于最后一个下标，说明可以到达最后一个下标，返回truereturn true;}}return false;
}}

复杂度分析：

时间复杂度为 O(n)，其中 n 是数组的长度。因为我们只需遍历一次数组即可判断能否到达最后一个下标。
空间复杂度为 O(1)，我们只需要保存一个额外的变量 maxPos。

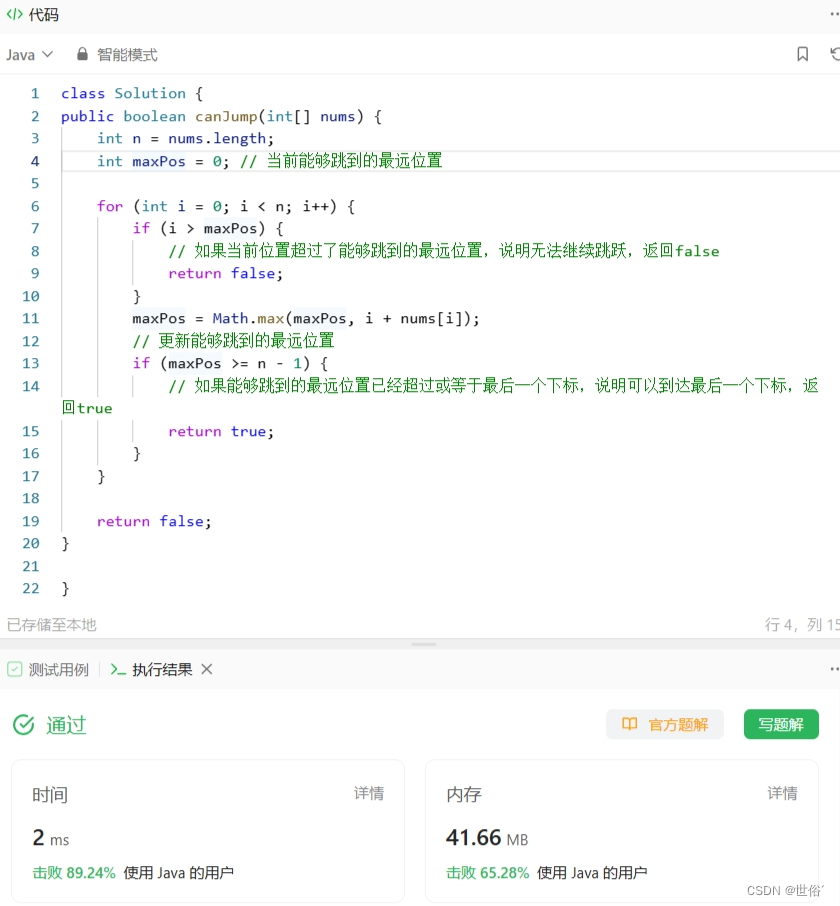
LeetCode运行结果：

方法二：动态规划

除了贪心之外，还可以使用动态规划来解决这个问题。

该算法使用动态规划的思想，定义一个布尔型数组 dp，其中 dp[i] 表示能否从第0个位置跳到第i个位置。

为了计算 dp[i]，我们从前往后遍历数组中的每个位置 i，并在其中再次遍历所有位置 j < i。只有当某个位置 j 可以到达，并且从 j 位置可以到达 i 位置时，才有可能到达 i 位置。因此，如果存在一个位置 j 满足条件，即 dp[j] && j + nums[j] >= i，则说明当前位置 i 可以到达，我们将 dp[i] 设置为 true。最终返回 dp[n-1] ，表示能否从第 0 个位置跳到最后一个位置。

class Solution {
public boolean canJump(int[] nums) {int n = nums.length;boolean[] dp = new boolean[n]; // dp[i] 表示能否从第0个位置跳到第i个位置dp[0] = true; // 第0个位置一定可以到达for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (dp[j] && j + nums[j] >= i) {// 如果前面某一个位置可以到达，并且这个位置可以到达i，那么说明i也可以到达dp[i] = true;break;}}}return dp[n - 1];
}
}

复杂度分析：

时间复杂度为 O(n^2)，因为在计算 dp[i] 时，需要遍历之前的所有位置 j，所以总共需要进行 n * (n-1) / 2 次比较。
空间复杂度方面，动态规划算法使用了一个长度为 n 的数组 dp，所以空间复杂度为 O(n)。

与贪心算法相比，动态规划算法的时间复杂度较高，但是更加直观易懂，且可以解决更一般化的跳跃游戏问题。

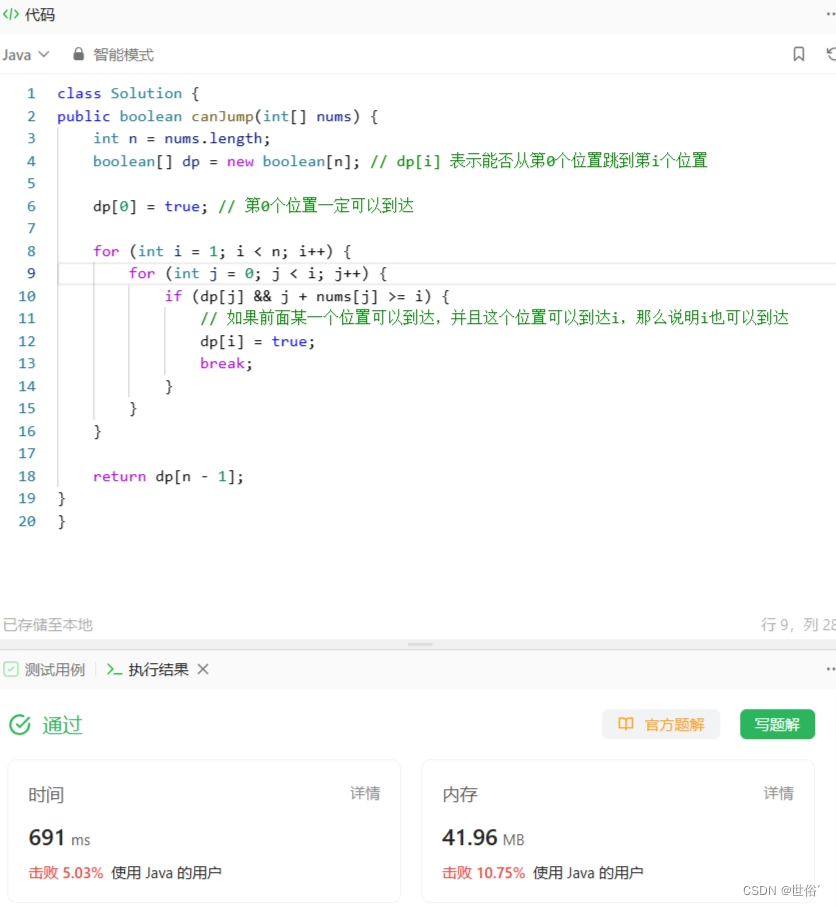
LeetCode运行结果：

方法三：回溯算法

除了贪心算法和动态规划算法，还可以使用回溯算法来解决跳跃游戏问题。

该算法使用回溯的思想，在每个位置上探索所有可能的跳跃，直到找到能到达最后一个位置的路径，或者发现无法到达的情况。

具体实现中，我们定义一个辅助函数 backtrack，其中 position 参数表示当前所在的位置。首先，在每个位置上计算能够跳跃到的最远位置 furthestJump，然后从最远位置开始反向遍历，尝试从当前位置跳到下一个位置 nextPosition，并递归调用 backtrack 函数。如果最终找到一条路径能够到达最后一个位置，则返回 true；如果所有尝试都失败，则返回 false。

class Solution {
public boolean canJump(int[] nums) {return backtrack(nums, 0);
}private boolean backtrack(int[] nums, int position) {// 到达最后一个位置，返回 trueif (position == nums.length - 1) {return true;}int furthestJump = Math.min(position + nums[position], nums.length - 1);for (int nextPosition = furthestJump; nextPosition > position; nextPosition--) {if (backtrack(nums, nextPosition)) {return true;}}return false;
}}

复杂度分析：

回溯算法的时间复杂度是指数级的，因为在每个位置上都会进行多次递归调用。具体来说，在最坏情况下，即每次跳跃只能跳一个格子，需要进行 n 层递归调用，每层调用需要遍历 nums 数组中的所有元素，因此总时间复杂度是 O(n^n)。

空间复杂度主要取决于递归调用栈的深度，最坏情况下，递归调用栈的深度为数组的长度，所以空间复杂度为 O(n)。

尽管回溯算法能够找到所有可能的路径，但由于其指数级的时间复杂度，对于较大的输入可能会导致超时。因此，在实际应用中，贪心算法和动态规划算法更常用和高效。

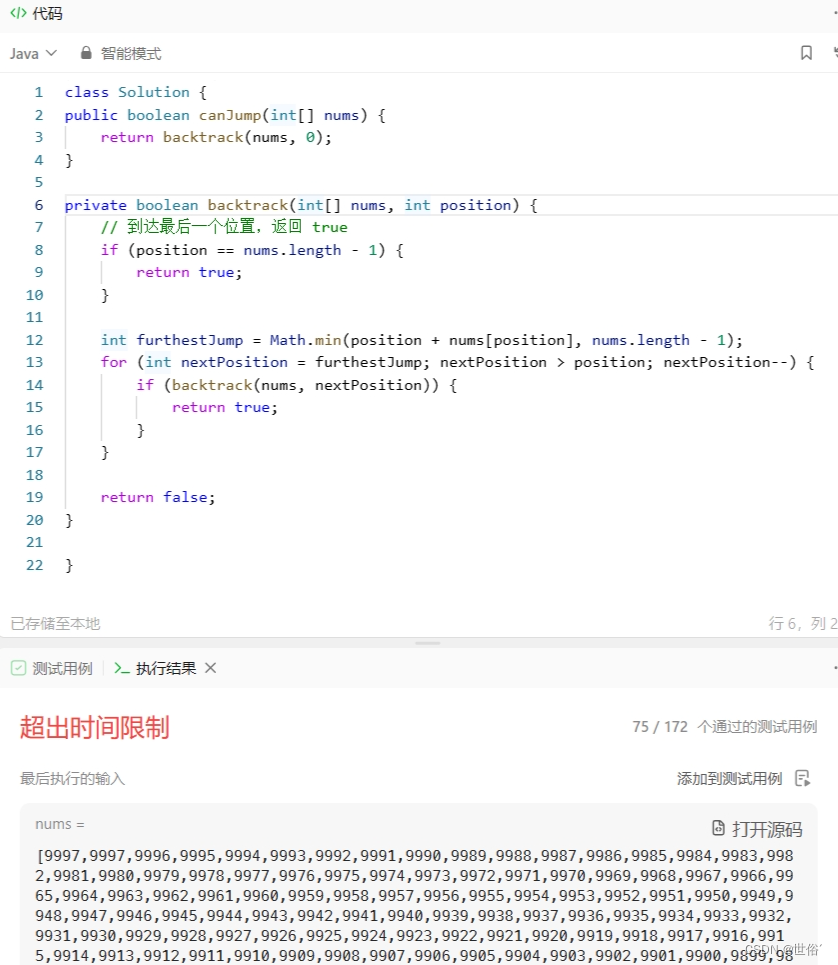
LeetCode运行结果：

方法四：并查集

除了贪心算法、动态规划、回溯算法，还可以使用特殊的数据结构来解决跳跃游戏问题，例如并查集。

并查集是一种用于处理元素分组和查找连通性的数据结构。在跳跃游戏问题中，我们可以将每个位置看作一个节点，并按照能够跳跃到的下一个位置建立连通关系。

在实现中，我们首先定义了一个并查集类 UnionFind，其中包含 find、union 和 isConnected 等操作。在构造函数中，将每个位置初始化为其自身的根节点。

接下来，遍历数组 nums 中的每个位置，并计算出从当前位置能够跳跃到的最远位置 maxJump。然后，将当前位置与从 i+1 到 maxJump 的位置进行合并操作，表示它们之间存在连通关系。

最后，判断起点位置 0 和终点位置 n-1 是否连通，即可得出是否能够跳跃到终点位置。

class Solution {
class UnionFind {int[] parent;public UnionFind(int n) {parent = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;}}public int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}public void union(int x, int y) {int rootX = find(x);int rootY = find(y);if (rootX != rootY) {parent[rootX] = rootY;}}public boolean isConnected(int x, int y) {return find(x) == find(y);}
}public boolean canJump(int[] nums) {if (nums == null || nums.length == 0) {return false;}int n = nums.length;UnionFind uf = new UnionFind(n);for (int i = 0; i < n; i++) {int maxJump = Math.min(i + nums[i], n - 1);for (int j = i + 1; j <= maxJump; j++) {uf.union(i, j);}}return uf.isConnected(0, n - 1);
}}

复杂度分析：

时间复杂度：O(n^2)，其中 n 是数组的长度。需要进行两层循环，对每个位置都进行合并操作。
空间复杂度：O(n)，需要使用一个并查集来保存每个位置的根节点。

需要注意的是，并查集不适用于所有类型的跳跃游戏问题，只适用于某些特定情况下。在一般情况下，仍然推荐使用贪心算法、动态规划或回溯算法来解决跳跃游戏问题。

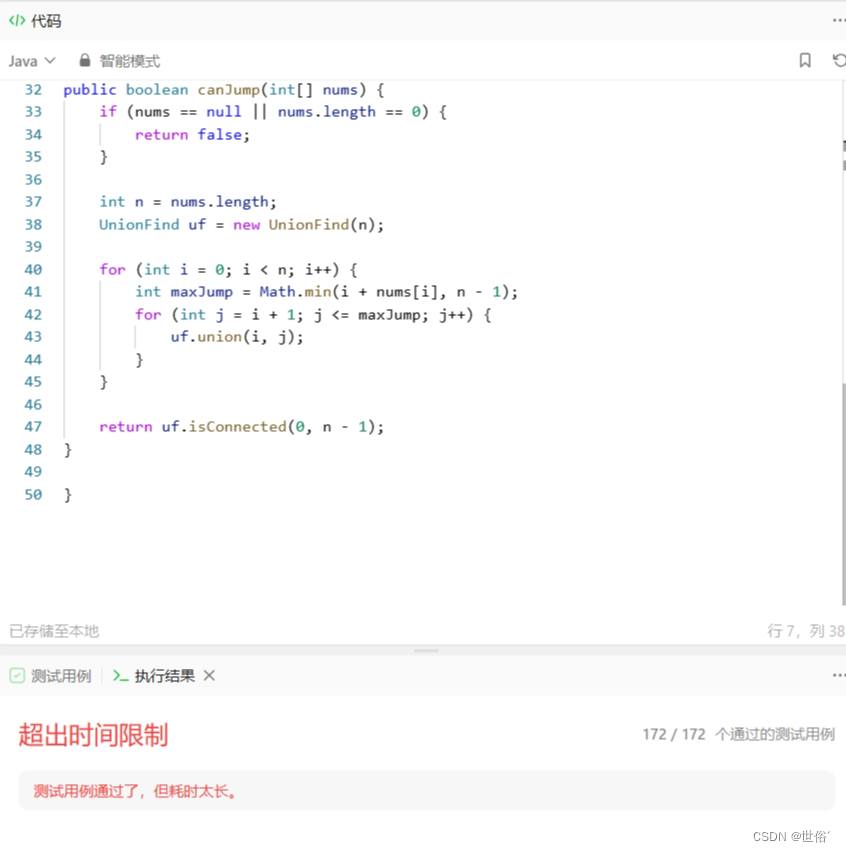
LeetCode运行结果：

第二题

题目来源

56. 合并区间 - 力扣（LeetCode）

题目内容

解决方法

方法一：排序和遍历

这个问题可以使用排序和遍历的思路来解决。

首先，我们对给定的区间集合按照起始位置进行排序。这样可以确保如果有重叠的区间，它们会相邻。
然后，我们遍历排序后的区间集合，并维护一个当前合并区间的起始位置 start 和结束位置 end。初始时，我们将第一个区间的起始位置和结束位置分别赋值给 start 和 end。
接下来，我们从第二个区间开始遍历，比较当前区间的起始位置与当前合并区间的结束位置。如果当前区间的起始位置大于当前合并区间的结束位置，说明当前区间与前面的区间没有重叠，我们可以将当前合并区间 [start, end] 加入结果数组中，并更新 start 和 end 为当前区间的起始位置和结束位置。
否则，如果当前区间的起始位置小于等于当前合并区间的结束位置，说明当前区间与前面的区间有重叠，我们可以更新当前合并区间的结束位置为当前区间的结束位置。这样就实现了区间的合并。
最后，遍历完成后，将当前合并区间 [start, end] 加入结果数组中即可。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;class Solution {public int[][] merge(int[][] intervals) {if (intervals.length <= 1) {return intervals;}// 按照区间的起始位置进行排序Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));List<int[]> merged = new ArrayList<>();int start = intervals[0][0];int end = intervals[0][1];for (int i = 1; i < intervals.length; i++) {int intervalStart = intervals[i][0];int intervalEnd = intervals[i][1];if (intervalStart <= end) {// 当前区间和前面的区间有重叠，更新当前合并区间的结束位置end = Math.max(end, intervalEnd);} else {// 当前区间和前面的区间没有重叠，将当前合并区间加入结果数组中merged.add(new int[]{start, end});// 更新当前合并区间为当前区间start = intervalStart;end = intervalEnd;}}// 将最后一个合并区间加入结果数组中merged.add(new int[]{start, end});return merged.toArray(new int[merged.size()][]);}
}

复杂度分析：

排序的时间复杂度为O(n log n)，其中 n 是区间的数量。这是因为我们对区间进行了一次排序操作。接下来，我们遍历排序后的区间集合，每个区间只会被访问一次。因此，遍历的时间复杂度是O(n)，其中 n 是区间的数量。最后，将合并后的区间转换为结果数组的过程需要O(n)的时间复杂度，其中 n 是合并后的区间数量。综上所述，算法的总时间复杂度为O(n log n) + O(n) + O(n) = O(n log n)。
对于空间复杂度，我们使用了一个结果集合来存储合并后的区间，其大小最多为n。因此，空间复杂度为O(n)。

注意，这里不考虑返回结果的空间复杂度。如果按照题目要求返回二维数组作为结果，该空间复杂度为O(n)。

LeetCode运行结果：

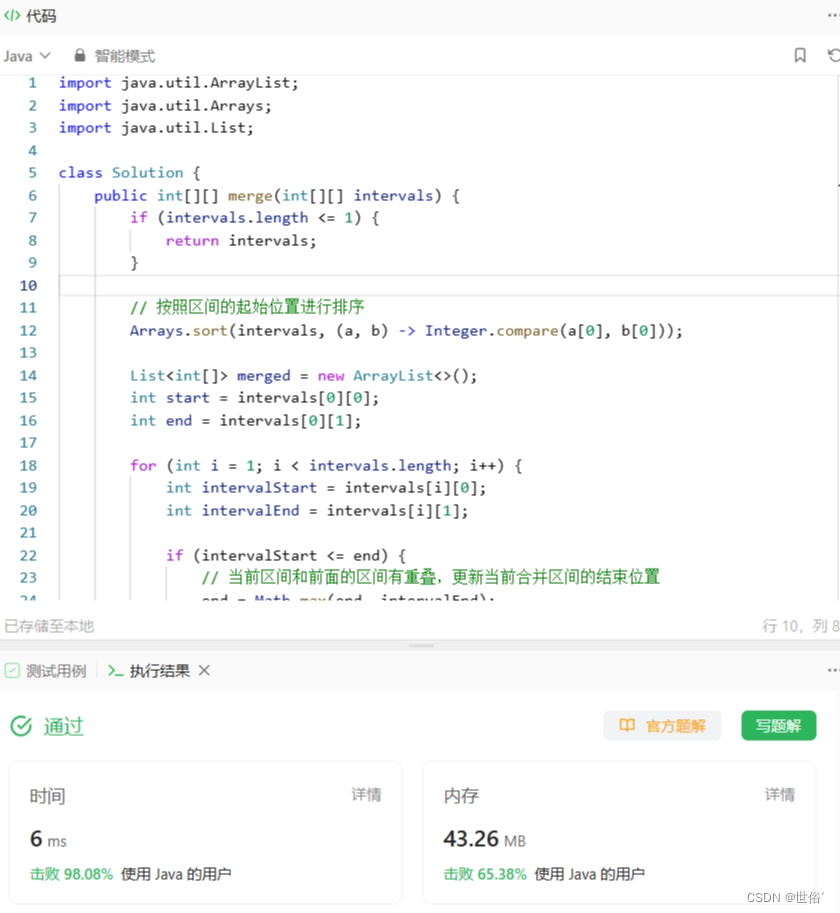
方法二：扫描线算法

除了排序和遍历的方法，还可以使用扫描线算法来合并区间。这种方法在处理区间重叠的问题时也很高效。

首先，我们将所有区间的起始点和结束点提取出来，并分别存储在两个数组中。对于每个点，我们还需要记录它是一个起始点还是结束点。
然后，我们对这些点进行排序，并使用一个变量 count 来记录当前遍历到的起始点的个数。同时，我们还需要用一个变量 start 来记录当前合并区间的起始位置。
接着，我们从左到右遍历这些点，并根据每个点的类型来更新 count 的值。当遇到起始点时，说明有一个新的区间开始了，因此 count 加1。当遇到结束点时，说明一个区间结束了，因此 count 减1。
在遍历过程中，每当 count 的值从0变为1时，说明一个新的合并区间开始了，我们将当前点的位置赋值给 start。每当 count 的值从1变为0时，说明一个合并区间结束了，我们将当前点的位置作为这个区间的结束位置，并将合并区间 [start, end] 加入结果数组中。
最后，我们就可以得到合并后的区间。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;class Solution {public int[][] merge(int[][] intervals) {if (intervals.length <= 1) {return intervals;}int n = intervals.length;// 提取所有点的值和类型int[] points = new int[2 * n];int[] types = new int[2 * n];for (int i = 0; i < n; i++) {points[2 * i] = intervals[i][0];types[2 * i] = 1; // 起始点points[2 * i + 1] = intervals[i][1];types[2 * i + 1] = -1; // 结束点}// 对点进行排序Integer[] indices = new Integer[2 * n];for (int i = 0; i < 2 * n; i++) {indices[i] = i;}Arrays.sort(indices, (a, b) -> {if (points[a] != points[b]) {return Integer.compare(points[a], points[b]);}return Integer.compare(types[b], types[a]);});List<int[]> merged = new ArrayList<>();int count = 0;int start = 0;for (int index : indices) {int point = points[index];int type = types[index];if (count == 0) {start = point;}count += type;if (count == 0) {int end = point;merged.add(new int[]{start, end});}}return merged.toArray(new int[merged.size()][]);}
}

复杂度分析：

算法的时间复杂度为O(n log n)，其中n是区间的数量。这是因为算法涉及对区间的排序操作，而排序的时间复杂度为O(n log n)。
算法的空间复杂度为O(n)，用于存储排序后的区间和合并后的结果。

需要注意的是，在最坏情况下，即所有的区间都不重叠时，算法需要将所有区间都合并为一个大区间，此时时间复杂度为O(n)。

总之，本算法的时间复杂度和空间复杂度都是比较优秀的，是解决区间合并问题的一个非常好的算法。

LeetCode运行结果：

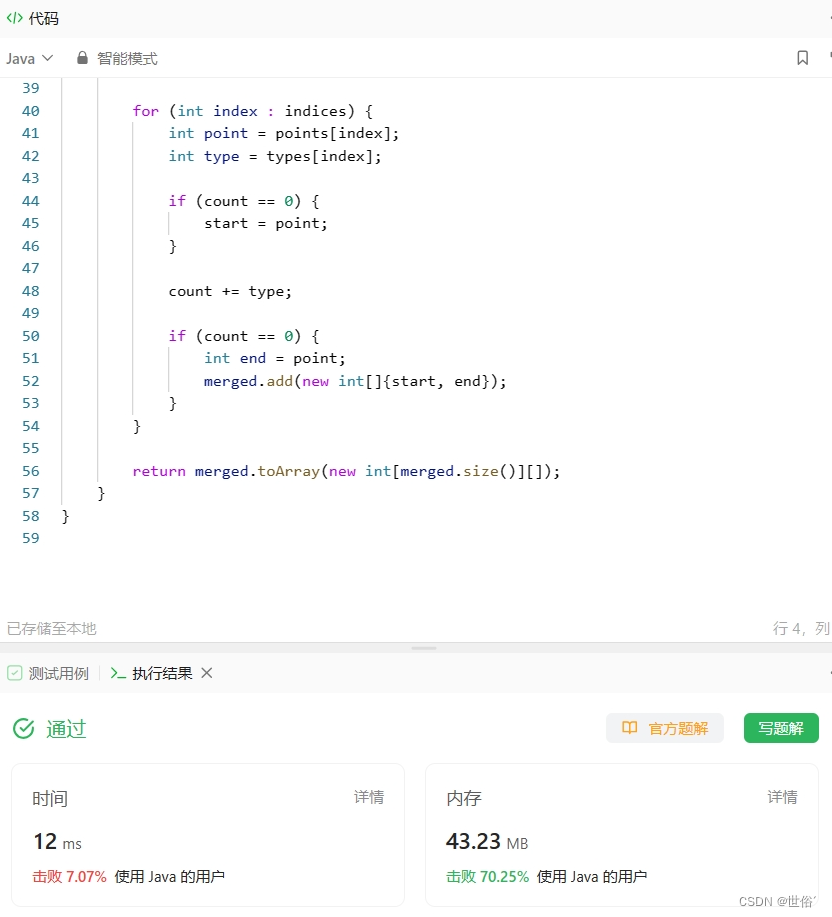
方法三：栈

除了排序和遍历、扫描线算法外，还有一种常见的方法是使用栈来合并区间。

具体实现思路如下：

首先将所有区间按照起始位置进行排序。
创建一个栈，将第一个区间放入栈中。
遍历剩余的区间，如果当前区间的起始位置大于栈顶区间的结束位置，说明两个区间不重叠，直接将当前区间入栈。否则，将当前区间与栈顶区间合并，更新栈顶区间的结束位置为两者中的较大值。
遍历完所有区间后，栈中存储的就是合并后的区间。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;class Solution {public int[][] merge(int[][] intervals) {if (intervals.length <= 1) {return intervals;}// 根据起始位置对区间进行排序Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));// 使用栈来合并区间Stack<int[]> stack = new Stack<>();stack.push(intervals[0]);for (int i = 1; i < intervals.length; i++) {int[] currentInterval = intervals[i];int[] topInterval = stack.peek();if (currentInterval[0] > topInterval[1]) {// 当前区间与栈顶区间不重叠，直接入栈stack.push(currentInterval);} else {// 合并当前区间和栈顶区间topInterval[1] = Math.max(topInterval[1], currentInterval[1]);}}// 将栈中的区间转化为数组返回List<int[]> merged = new ArrayList<>(stack);return merged.toArray(new int[merged.size()][]);}
}

复杂度分析：

使用栈的方法时间复杂度取决于排序的时间复杂度，因此为 O(n log n)，其中n是区间的数量。空间复杂度为O(n)，用于存储合并后的区间。

具体分析如下：

对区间进行排序的时间复杂度为 O(n log n)，因为我们需要对所有区间按照起始位置进行排序。
遍历整个区间数组的时间复杂度为 O(n)，因为我们只需要遍历每个区间一次，并将合并后的区间存储在一个栈中。
最后将栈中的元素转化为二维数组的时间复杂度为 O(n)，因为我们需要遍历栈中所有元素一次，并将它们存储在一个二维数组中。

因此，总的时间复杂度为 O(n log n) + O(n) + O(n) = O(n log n)。空间复杂度为O(n)，因为我们需要存储合并后的区间。

需要注意的是，排序操作是这种方法的时间复杂度瓶颈，因此如果输入区间已经有序或者近似有序，则使用这种方法可能更加高效，因为排序的时间复杂度可以达到O(n)。但是一般情况下，排序和遍历、扫描线算法仍然是解决区间合并问题的首选方法。

LeetCode运行结果：

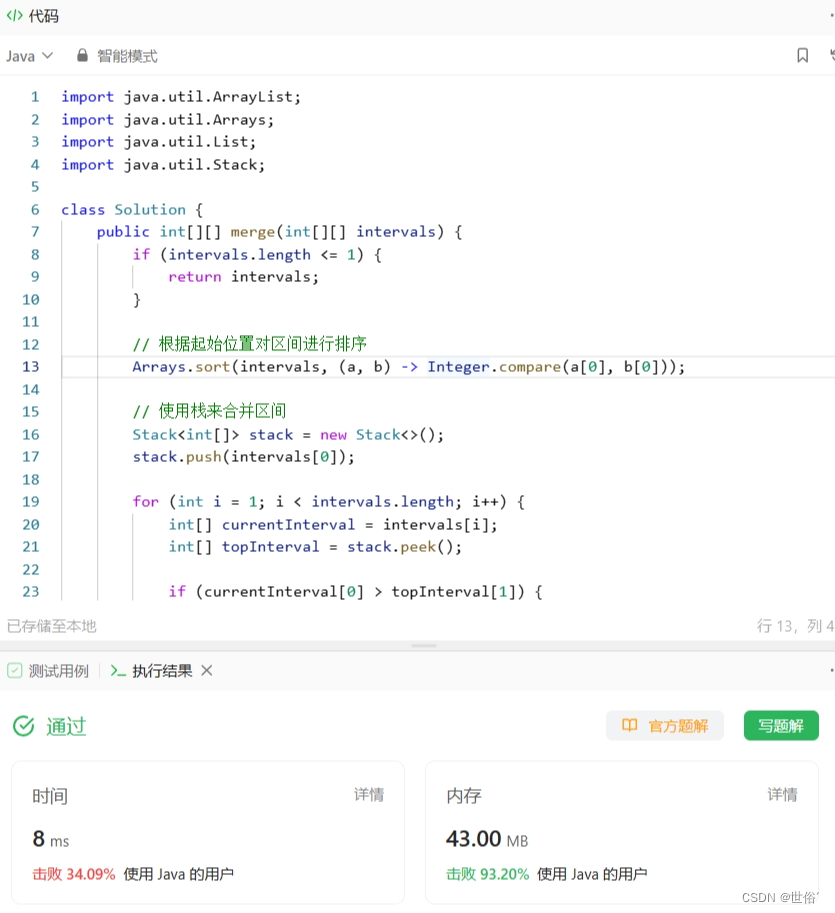
第三题

题目来源

57. 插入区间 - 力扣（LeetCode）

题目内容

解决方法

方法一：遍历和比较

思路与算法：

首先，根据题目要求，我们可以将给定的区间列表按照起始端点进行排序，这样可以方便后续的处理。
接下来，我们需要遍历排序后的区间列表，逐个与新的区间进行比较和合并。
初始化一个结果列表 merged，用于存储最终的合并后的区间。
遍历排序后的区间列表，对于每个区间 intervals[i]，与新的区间 newInterval 进行比较和合并。
- 如果 intervals[i] 的结束位置小于 newInterval 的起始位置，说明两个区间没有重叠，直接将 intervals[i] 加入 merged 中。
- 如果 intervals[i] 的起始位置大于 newInterval 的结束位置，说明后面的区间也不会有重叠，直接将 newInterval 和后面的区间加入 merged 中，并返回最终结果。
- 如果 intervals[i] 和 newInterval 存在重叠，我们需要不断地更新 newInterval 的范围，使其包括当前区间 intervals[i] 及可能的后续重叠区间，直到找到一个不与 newInterval 重叠的区间或者完成遍历。
最后，将 newInterval 添加到 merged 中，并将剩余的 intervals[i] 依次加入 merged。
返回 merged 列表中的区间数组作为最终结果。

import java.util.ArrayList;
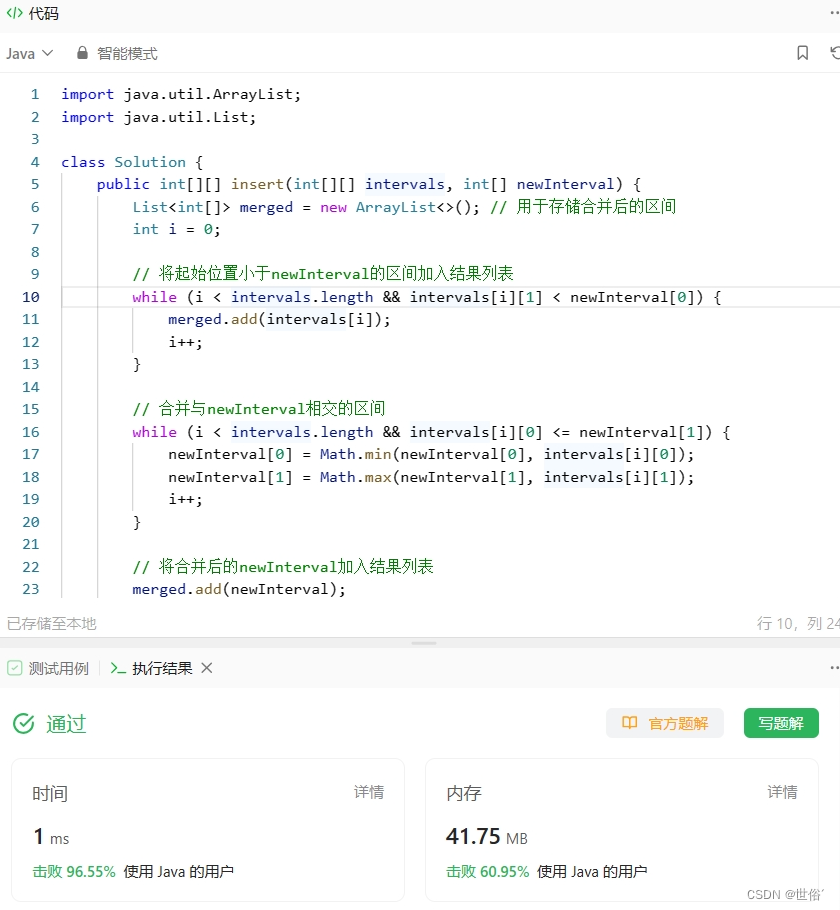
import java.util.List;class Solution {public int[][] insert(int[][] intervals, int[] newInterval) {List<int[]> merged = new ArrayList<>(); // 用于存储合并后的区间int i = 0;// 将起始位置小于newInterval的区间加入结果列表while (i < intervals.length && intervals[i][1] < newInterval[0]) {merged.add(intervals[i]);i++;}// 合并与newInterval相交的区间while (i < intervals.length && intervals[i][0] <= newInterval[1]) {newInterval[0] = Math.min(newInterval[0], intervals[i][0]);newInterval[1] = Math.max(newInterval[1], intervals[i][1]);i++;}// 将合并后的newInterval加入结果列表merged.add(newInterval);// 将剩余的区间加入结果列表while (i < intervals.length) {merged.add(intervals[i]);i++;}// 将结果列表转换为数组返回return merged.toArray(new int[merged.size()][2]);}
}

复杂度分析：