联合概率P(A∩B)

两个事件一起（或依次）发生的概率。

例如：掷硬币的概率是 ¹⁄₂ = 50%，翻转 2 个公平硬币的概率是 ¹⁄₂ × ¹⁄₂ = ¹⁄₄ = 25%（这也可以理解为 50% 的 50%）

对于 2 个硬币，样本空间将是 4 {HH,HT,TH,TT}，如果第一个硬币是 H，那么剩余的结果是 2 {HT,HH}。这意味着第一个事件可能会影响第二个事件。

例如：从 10 个不同颜色的球中选出 1 个绿球的概率是 ¹⁄₁₀， 10个球中选2个绿球的概率（2个绿、2个蓝、2个红、4个黄）²⁄₁₀ × ¹⁄₉（这个排列组合会更清楚）

简而言之。当第一个事件的发生影响第二个事件的发生时，它们是相关事件。

这里，P(B|A) 被读作 在 A 之后发生 B 的概率。这是当 A 事件已经发生时发生 B 事件的概率。这称为条件概率。

联合概率和条件概率

例：城市中的一个三角形区域被化学工业污染。有2%的孩子住在这个三角区。其中 14% 的检测过量有毒金属呈阳性，而不在三角区居住的城市儿童的阳性检测率仅为1%。

考虑：T 表示居住在三角形区域的人，并且P 表示检测呈阳性的人。

当它说区域中 14% 的孩子测试为阳性时，这意味着：如果从三角形中随机抽取一个孩子，它将有 14% 的机会测试为阳性。这是 P(P∣T)

P(P∩T) 的解释是自整个人口中随机选择后即在三角形中并且测试为阳性的概率。

用维恩图理解

P(A∩B) 是 A 和 B 都发生的概率（没有任何附加信息。）

P(A|B) 是如果我们知道 B 已经发生，A发生的概率。

让我们通过一个例子来理解它。一个班有60名学生。33个喜欢蓝色，23个喜欢红色，20个学生喜欢这两种颜色，4个学生喜欢橙色。

1. 选出一个同时喜欢红和蓝颜色的学生的概率是多少？

这非常简单：P(B ∩ R) = ²⁰⁄₆₀

2. 从喜欢红色的学生中选出一个喜欢蓝色的学生的概率是多少？

我们将检查从特定学生集中选择具有特定选择的学生的概率。

⇒ 喜欢红色的学生有 23 人。其中有 20 个喜欢这两种颜色。

P(B | R) =²⁰⁄₂₃

通过维恩图和上面的例子，我们可以说在这两种情况下，事件的结果都没有改变，但样本空间正在减少。因此：

𝐏(𝐀∣𝐁) ≥𝐏(𝐀∩𝐁)

更多的例子

例子1：

 

假设掷两个骰子，第一个得到6第二个得到4的概率是多少? 假设掷两个骰子，如果两个骰子的数字之和是10，第二个骰子显示4的概率是多少?

在第一种情况下，没有给出定义样本空间的条件。所以我们从两个骰子中取可能的结果，也就是36。

P(a∩b) = 2/36

在第二种情况下，对于样本空间有一个条件，即骰子上的两个数的样本空间总和为10。样本空间的总元素只有3 {4+6,5+5,6+4}

P(a | b) = 1/3

例子2：

一个人正在过马路，我们想计算他被路过的汽车撞到的概率，这取决于交通灯的颜色。

设H代表这个人是否被撞，C代表红绿灯的颜色。

H ={撞,不撞}

C ={红、黄、绿}。

在这种情况下，你被撞到的条件概率是概率P(H=撞到|C=红色)，即假设灯是红色的，你被车撞到的概率有多大。

即使不是红灯，也有可能有人被撞到，但这里我们只考虑红灯时发生的车祸。

而联合概率则是P(H=撞到，C=红色)，即红灯亮时你被车撞到的概率。

假设一个人横穿马路 3 次而没有发生事故。但第7次被撞了。如果使用联合概率，我们还想知道当他被撞时灯是红色的概率是多少。

现在如果我们说，他在红灯时过马路10次，被车撞了7次。在这种情况下，样本空间的条件是已经给定的。

例子3：

研究人员调查了100名学生，询问他们最想拥有哪种超能力。这个双表格显示了参与调查的学生样本的数据:

我们来找出不同的概率：

1. 找出学生选择飞行作为他们超能力的概率。

没有给出样本空间的条件。我们取所有学生(100)来计算概率。

P(fly) = 38/100 = 0.38

2. 求出该学生是男性的概率。

同样，没有给出样本空间的条件。我们取所有学生(100)来计算概率。

P(male)= 48/100 = 0.48

3. 求选择飞行作为超能力时，这个学生是男性的概率。

这很有趣，这个问题的样本空间是一群想要飞行的学生。n (S) = 38，38名学生中有26名是男性。所以:

P(male∣fly) = 26/38 = 0.68

或者用条件概率公式：

P(male∩fly) =选择飞行男生/总人数= 26/100

P(male∣fly)= P(male∩fly)/ P(fly)= 26/38 = 0.68

4. 假设该学生是男性，求出该学生选择飞行的概率。

这和上一题差不多。这个问题的样本空间为n(S) = 48。在48名学生中，有26人选择飞行。所以：

P(male∣fly) = 26/48 =0.68

5、I代表一个学生选择隐身作为超能力的事件，F代表一个学生是女性的事件。

解释P(I∣F)≈0.62的含义;

• 大约62%的女性选择隐身作为她们的超能力。

• 在选择隐身作为自己超能力的人中，大约有62%是女性。

解释如下：

n(S) =所有女性，I∣F可以被解读为在所有女性中选择隐身的人。

总的来说，我们可以理解为大约62%的女性选择隐身作为她们的超能力。所以表述a是正确的。

例子4：

下表是将各国按地区和平均创业成本(占某一年人均国民总收入(GNI)的百分比)进行了分类。

考虑到如果该国的创业成本归类为高，那么找出该国位于南亚地区的概率。

这个问题属于条件概率，因为给定了选择样本空间的条件：创业成本高的国家 n(S) = 87（样本空间），  以上样本空间中的南亚地区国家，即创业成本高的国家：7

所以，从创业成本高的国家中选择南亚地区国家的概率= 7/87

如果我们用条件概率的公式：

我们可以先计算 P(A ∩ B)，即从所有南亚地区且创业成本高的国家中选择一个国家的概率。

 

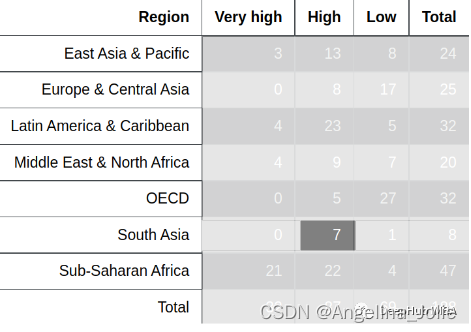
这样的国家有7个。由于没有定义选择样本空间的条件，我们将采用全部空间，即 n(S) = 188。

P(A ∩ B) = 7/188

现在，我们需要计算一个国家创业成本高的概率。这很简单：

P(A) = 87/188

使用公式 得到P(B|A) = 7/87