前言
之前介绍了 位图,位图在判断某一个 数是否存在,或者在计算某个数是否出现 一次 或者 两次这些问题之上有着非常高效的实现复杂度,它的时间复杂度 可以达到 O(1),因为都是逻辑判断和 ,常数次计算。具体请看博客:C++ - 位图 - bitset 容器介绍_chihiro1122的博客-CSDN博客
但是位图的局限性也很高,对于 int ,size_t 这些类型,可以直接映射比特位的下标,来看这个比特位的值是 1 还是 0 ,但是 如果是 string 这种自定义类型,就会出现问题。
比如string类,我们可以按照hash 当中对 string值 计算出的 hash 值来在位图当中进行 映射,但是,string 在计算哈希值的时候,它不想 int 类型,是多少就是多少,一个 string 类 映射出的 hash 值,可能有多个 string 类都会使用这个值:具体的实现逻辑,可以看看下面博客当中对 闭散列开放式地址法哈希表当中对 仿函数的书写:C++ - 开放地址法的哈希介绍 - 哈希表的仿函数例子_chihiro1122的博客-CSDN博客
当某一个 string计算出的 hash 值和 另一个 string计算出的hash值相同,那么我们在利用这个hash 值寻找 某个 string的时候就会出现误判,比如我想找第一个 string是否存在,原本是不存在的,但是第二个 string存在,就把 位图当中 对应位置的 比特位 修改为 1 了,那么在查找过程当中,我就认为第一个 string是存在的,但是实际上不存在。这就 造成了 结果的误判。
此时,string 不在是准确的,但是 在可能是误判的。
string 类计算出 hash 值有多种方式可以解决,虽然都可以缓解冲突问题,但是没有更本上解决 冲突问题,最终还是会发生冲突,所以,位图是不能解决 string 类的。
这时有一个布隆的人就提出了布隆过滤器。
布隆过滤器
布隆这个人就想,能不能降低 误判的概率。
举个例:在线下和朋友面基的时候,我们要在一个商场当中找到我们的朋友,朋友跟你说,它穿了白色的T恤,黑色的牛仔裤,那么商场当中人这么多,穿同样衣服的人很有可能不止 朋友一个,那么此时就会出现误判,可能就会找错人。
那么 布隆就想,能不能让朋友在给出关于自己更详细 的信息,比如在给出 身高,发型,身材胖瘦,那么我就可以再根据这些信息,在筛选出一些人,那么我 误判的概率就会有所降低。
这就是 布隆过滤器所实现的效果。
但是,不管你提供的信息有多么详细,极端情况下,可能还是会有人和朋友的特征发生冲突,让你找错人,但是,这种情况在信息详细的情况下很难发生,所以,给出详细的信息虽然不能彻底解决冲突的问题,但是还是可以很大程度上的实现 降低误判的概率。
比如现在,我们判断 四个 公司是否参加 某一个 活动,那么,我们对这四个公司的公司名是否存在在名单上进行判断,而且,我们不在使用 一个字符串映射一个位置的方式来计算了,假设我们现在使用 三个位置来映射,三个位置为1 ,才说明这个公司参加了这次活动,其中有任何一个位置为 0 都没有参加:

如上述所示,除了华为之外,其他的都参加了,因为只有华为 有一个位置的映射是 0 ,我们发现,虽然华为和腾讯 阿里 的 两个位置冲突了,但是我们可以正确的判断华为是否参加了这场活动。
像上述就降低了 误判率,但是没有彻底消除误判,可能后面还会有公司和 华为的第三个映射位置冲突,但是我们发现这种方式可能有效的 降低误判率,而且向上述的方式,一个 string 映射的位置越多,那么误判率降低的也就越多。
此时 ,string类 不在是准确的,在可能是误判的。
而且,如果一个 string 占用的 映射位置变多了,就会带来一个问题,就是空间利用率降低了,也就是说,使用布隆过滤器的话,如果降低误判率,就会降低空间利用率;反之。
布隆过滤器实现
布隆过滤器的实现,直接利用位图作为底层,然后在之上实现过滤条件即可。具体 位图的实现可以上篇文章:C++ - 位图 - bitset 容器介绍_chihiro1122的博客-CSDN博客
或者使用库当中的 bitset 实现。
位图实现的代码:
#pragma once
#include<vector>namespace bit
{template<size_t N>class bitset{public:bitset(){_a.resize(N / 32 + 1);}// x映射的那个标记成1void set(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] |= (1 << j);}// x映射的那个标记成0void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _a[i] & (1 << j);}private:vector<int> _a;};按照上述的说法,一个 string 需要三个比特位来就映射,当三个位置都是 1 ,才能说明这个string是存在的。
关于string计算hash 值有很多方法,具体可以参考这篇文章:各种字符串Hash函数 - clq - 博客园 (cnblogs.com)
那么,关于一个 string 类型的三个映射位置,我们把每一个映射位置,都用不同的 hash 计算方式来映射,当然三种映射方式都有可能冲突,但是,要三个位置都冲突的话,这种可能性比较小。
当我们要“插入”一个 string时, 就 计算三种映射方式,计算出三个对应位置,把这三个位置 set为1 即可。
判断是否存在的test()函数,只需要判断这个 string 用三个方法计算出的 三个位置是否都为 1,是就存在,不是就不存在。
在布隆过滤器当中,我们不敢去支持 rset()删除函数,因为一个 string 是映射了三个位置的,如果我们直接把这个三个比特位的值改为 0 的话,那么 如果有其他的 string 某个位置映射到 这三个 位置的话(也就是说冲突),我们就会修改到 其他string 的映射位置,那么这个 本来是存在,但是在 rset()另一个 string 之后,这个 string 就不存在了,这个问题很大。
而且我们很难确定一个 位置 映射了 那些字符串,所以我们一般不支持删除函数。
如果想要支持的话,那么上述的三个位置就不仅仅是一个 比特位了,每一个位置要存储 这个位置映射了多少个 string,当我们要 rset()删除某一个 string的时候,就把这个 string 映射的三个位置的计数--,但是计数就带来一个新的问题,如果单独是 2,3 个 比特位能存储的数字太有限了,而平常情况下,一个位置映射的string个数可能是 很多个 ,如果我们拿 8 个比特位来存储的话,最大就可以存储 0 - 2 ^ 8 范围的数据,但是 ,我们都用 位图来实现了,本来就是想利用位图节省空间的优点,那么我们在想上述来浪费空间的话,就有点本末倒置了。
有人专门对 使用的不同哈希函数的个数,误判率的影响,可以看下面这个篇文章:
详解布隆过滤器的原理,使用场景和注意事项 - 知乎 (zhihu.com)
这是文章当中数据测试的折线截图:
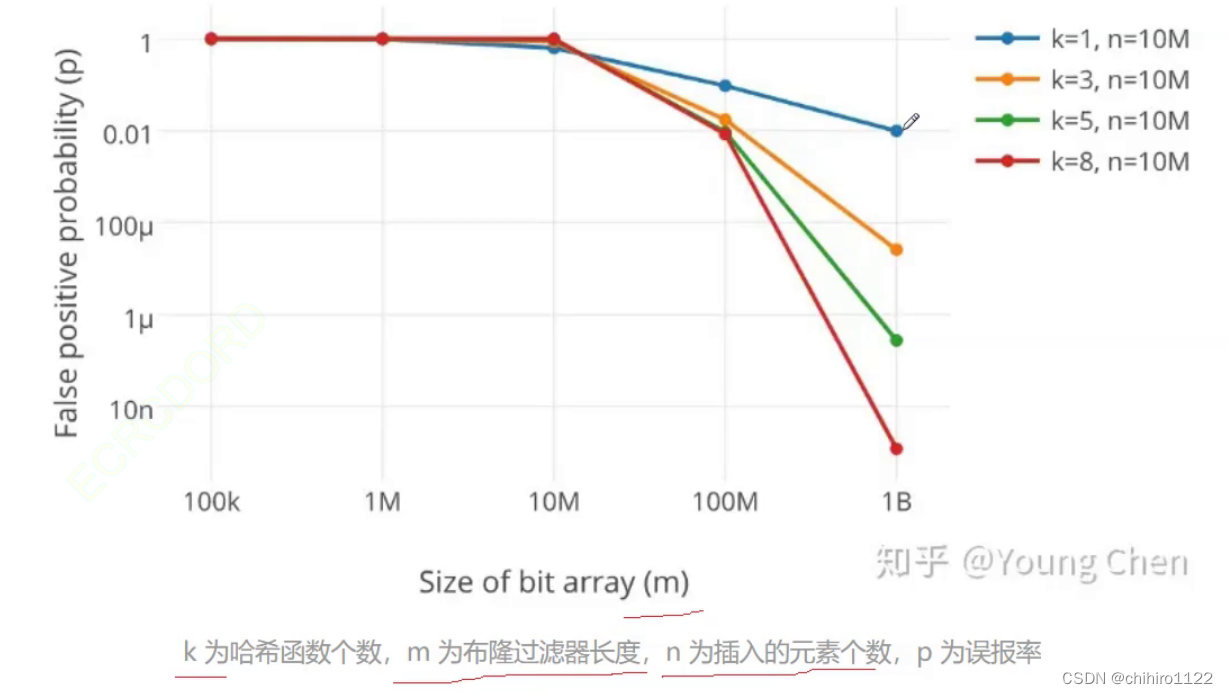
可以发现,当 k 越大 ,也就是当使用的不同哈希函数越多,那么左边的 误判率就越低。
m 是 位图的长度相对于 string 个数的比值,也就是相当于是 一个 string 要 映射m个比特位。上图当中是控制了 m 不变,按照每个 string 10个 比特位来映射的。
我们之前也分析过了,m 越多,误判率也就越低,但是空间利用率也就越低。
那么我们该如何选择其中的 m 和 k 呢?
在文章当中也描述了,按照下述公式计算:

总结下来,大约 m = n*4.3 是差不多和上述计算结果类似的。
布隆过滤器简单测试误判率
我们创建大量的字符串,这些字符串基本都是不同的,但是前缀有一部分是相同的,但是后缀不是基本不同的,然后我们来计算一下,这些例子,它的误判率有多少:
void TestBloomFilter2()
{srand(time(0));const size_t N = 100000;BloomFilter<N*8> bf;std::vector<std::string> v1;//std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";std::string url = "猪八戒";for (size_t i = 0; i < N; ++i){v1.push_back(url + std::to_string(i));}for (auto& str : v1){bf.Set(str);}// v2跟v1是相似字符串集(前缀一样),但是不一样std::vector<std::string> v2;for (size_t i = 0; i < N; ++i){std::string urlstr = url;urlstr += std::to_string(9999999 + i);v2.push_back(urlstr);}size_t n2 = 0;for (auto& str : v2){if (bf.Test(str)) // 误判{++n2;}}cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;// 不相似字符串集std::vector<std::string> v3;for (size_t i = 0; i < N; ++i){//string url = "zhihu.com";string url = "孙悟空";url += std::to_string(i + rand());v3.push_back(url);}size_t n3 = 0;for (auto& str : v3){if (bf.Test(str)){++n3;}}cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
}布隆过滤器的应用场景
1.不需要精确判断的场景,比如:快速判断某一昵称是够被注册过。

像这种场景之下,我们允许有很小的误判率,比如 3% - 5%,只需要用户输入的很大部分的用户名都能被正确的判断是否存在就行了,至于出现的那一小部分错误,用户也不知道,不用太在意。之所以使用 布隆过滤器是因为,他的底层实现逻辑还是 和 位图基本一致,只不过多加上了过滤的逻辑,所以,在查找方面,布隆过滤器还是和位图一样有着 非常高效的 常数级别的 时间复杂度,在用户输出用户名的时候,能很快的找出是否存在,不用子数据库当中去查找,虽然数据库的那种查找也非常的快,但是肯定是没有布隆过滤器快的。
而且,布隆过滤器,在可能会有误判,但是不在肯定是正确的,所以,不可能出现用户注册的用户名和 数据库当中的用户名注册重复情况。
2.在上述的场景下,还是判断用户名,但是需要精确和效率,也就是说不能直接用数据库来进行查找,因为数据库有点慢。
所以,此时就需要用 布隆过滤器 和 数据库结合的方式来使用了:
先用布隆过滤器查找一遍:
- 如果不在,因为不在是准确的,所以可以直接 打勾√ ;
- 如果在,因为在可能会误判,所以还要在数据库当中查找一遍,以数据库当中查找的结果返回给用户,在数据库当中查找肯定是精准的;
因为 布隆过滤器 查找的 时间复杂度是 O(1),所以,在上述的第二种情况,多判断的一次 布隆过滤器可能直接忽略不计。
这种方式,就减轻了数据库查找的负载压力,提升了效率。
哈希切分
我们先来看一个问题:
1. 给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法 和 近似算法
近似算法的话,看过前面的文章相信你已经猜到了,就是使用布隆过滤器,把 两个文件放到两个布隆过滤器当中,然后进行取交集的操作,取交集,在 上一篇当中对位图的介绍当中,已经进行说明,两者之间是类似,如有需要请看一下博客当中,对位图应用的板块介绍:
C++ - 位图 - bitset 容器介绍_chihiro1122的博客-CSDN博客
我们主要来看 精确算法:
query 是查询的意思,一句 sql 语句可能就是 30 个 字节(这里只是举一个例子),那么按照一个 query 是 30 字节的话,1G 是 2^30字节 ,大概是 10亿字节左右,那么 100 亿字节就是 大概 300G 左右。为我们只要 1G 的内存,所以 300 G 我们肯定是不可能完全存下的,所以我们要切分出一个一个的小文件,假设是 把 大文件 A 和 大文件 B 各自都切分成1000 个小文件,对这些小文件,按照 A 和 B 切分出的对应位置来进行一对一对的小文件进行比较,得出结果。
当然对于小文件当中的数据, 你可以按照哈希表的形式去处理,但是哈希表肯定是带来多余的内存消耗的,所以我们在这里不使用哈希表的方式来存储。
而且,我们按照顺序来切分出 的小文件,一个一个对比的话,效率也是不高的。以为 A 文件 和B 文件当中 query 的存储顺序不一定是一样的,我们可能不能再对应的小文件当中找到这个匹配的 query。假设,从 A 当中的第一个文件当中取出一个 query,那么假设这 query 在 B 当中是有交集的,但是在B 当中的 这个 query 可能在任意位置,那么平均切分的话,这 query可能在任意位置。那么也就意味,我想判断一个 query 在另一个文件当中是否有交集,就得把另一个大文件切分出的所有小文件都判断寻找一遍,那么这个效率就可想而知了。
所以,这里就需要哈希切分了。
还是同样把上述 两个大文件 都各自切成 1000 个小文件,从 大文件当中取出的 query,他其实本质是一个字符串,那么我们可以按照哈希当中对字符串转化成 key 的算法,算出字符串的 key 值,然后按照 key 值 % 1000(因为是1000个小文件),算出这个query是在 应该在哪一个 小文件当中存储,然后把 这query 放到对应文件当中。
同样,两个文件都进行同样的处理,如此下来,两个文件当中的query,都是按照同一个哈希函数进行有规律的排列的,那么此时,我们就只需要按照顺序(小文件匹配顺序)来一对一对的小文件进行取交集就行了。
如下图所示:

把两个文件按照 哈希函数去把 query 在 小文件当中进行存储。

此时去交集,就只需要按照 小文件对应编号来进行取交集就可以了。不需要像之前一样,找一个 query 需要遍历另一边的全部小文件。
我们把上述按照哈希函数来切分出来的一个个小文件,这样的操作叫做哈希切分。
使用哈希切分的话,在A和B 当中相同的 query 一定会进入 Ai 和 Bi 编号相同的小文件当中,但是不同的 query 可能会进入Ai 和 Bi 编号相同的小文件当中。不可能出现 相同的 query 进去到不同编号的 小文件当中。
上述描述的过程就和哈希桶一样,每一个哈希桶当中的数据,都是计算出来的key 值冲突的情况,在这个桶当中不止有 冲突的,还有相等的,那么这个相等的是一定存在的,冲突的才是不一定存在的。
而且,数据当中是有重复的部分的 ,也会是说我们要去重,那么在找交集的时候,Ai 读取出来 放到 set 当中去去重,然后再去和 Bi 文件当中进行比较,在不在,在就是交集然后要删掉Bi当中的query 防止交集重复,这是找交集的过程。
但是,我们在利用哈希切分,切分出来的一个一个小文件,因为这种方式不是 平均切分,我们上述之所以切分1000 份小文件,是因为,大文件是 300 G,那么平均切分出来每个小文件就是 300M,但是哈希切分不是平均的,是要计算 query 的 key 值,然后再去文件当中找位置。这种方式的话,可能会导致某一个文件特别大,某一个文件特别少。比如说一个文件当中,冲突数据太多,会导致 某个 Ai 文件太大,甚至超过 1G。
所以,这时候就要在对这个大的小文件再进行切分。但是,切分之后不一定就会满足要求,他可能还是比较大;比如在这个文件当中数冲突的数据占大部分,那么在切分,怎么切都是不能切小的。如下图所示:

对于上述情况,我们可以大可以换另一种哈希函数来防止冲突。
但是换哈希函数可能还会出现其他冲突,而且,他不能解决下述这种场景:

假设在上述的 Ai 小文件,总大小是 5G,其中没有正常数据,只有冲突数据和 相同的数据,其中 query 相同的占 4G,冲突的数据占1G。那么就算我们修改 哈希函数,那么也最多只能解决 1G 的大小,剩下 4G 是相同的query,计算出来的 key 值 不管用哪一个哈希函数,计算出的结果都是相同的。
解决方案:
- 先把 Ai 当中的query 读到一个 set 当中(先不进行切分(指的是二次切分),先进行读取),如果set 当中的 insert()报错抛出异常(bad_alloc),那就说明现在是 query 大多数都冲突的情况(不是大多数相等的情况);如果 insert ()能全部读出来,insert 当中 set 里面,那么就说明 Ai 当中就有大量的 重复 query。
- 如果抛出异常,说明有大量冲突,再换一个哈希函数即可,在进行二次切分。
2.给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址?
同样的,还是要进行 哈希切分,把大文件按照哈希函数 切分成一个个小文件。
此时,相同的文件一定进入了同一个小文件,我们再去用 map 来分别统计每一个小文件当中,每一个 ip 出现的次数,把最大的ip 和这个ip 出现次数保存起来。在去 统计下一个 ip。
至于 判断 一个小文件当中 ip 的最大值,有很多方法了,可以 用 小堆来实现。