使用Scipy优化梯度下降问题

目    录

问题重述

附加问题

步骤实施

1.查看Scipy官网SciPy，找到优化有关的模块（Optimize）

2.研究多种优化策略，选择最符合代码的方案进行优化

3.minimize函数参数及其返回值

4.代码展示

5.结果展示

6.进一步优化

6.1对如下函数方法进行优化

6.2基准测试

6.3 发现

测试文件附录

任务清单

问题重述

在二维平面有n个点，如何画一条直线，使得所有点到该直线距离之和最短

如果能找到，请给出其损失函数

附加问题

1.使用Scipy优化上述问题

2.主代码中不得出现任何循环语法，出现一个扣10分

步骤实施

1.查看Scipy官网SciPy，找到优化有关的模块（Optimize）

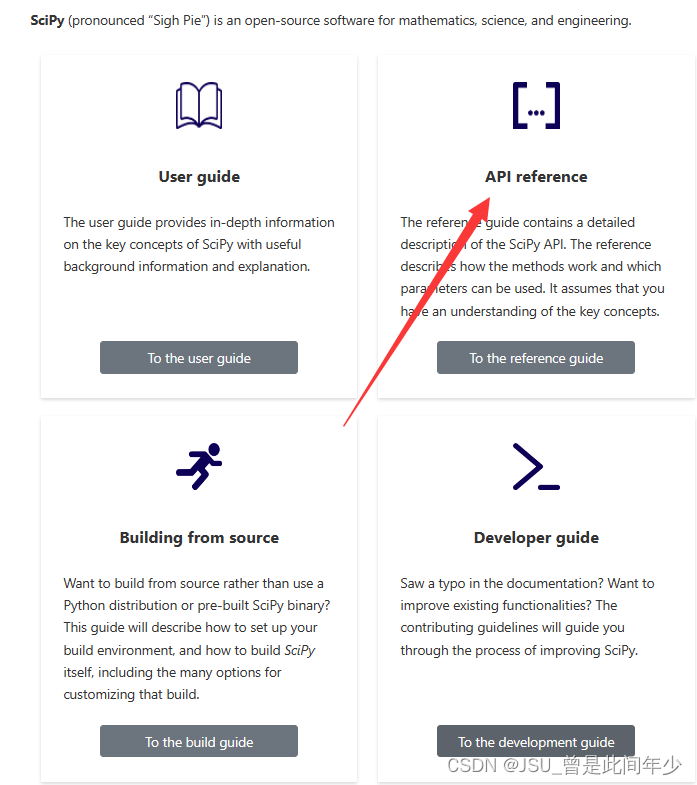
2.研究多种优化策略，选择最符合代码的方案进行优化

优化方法
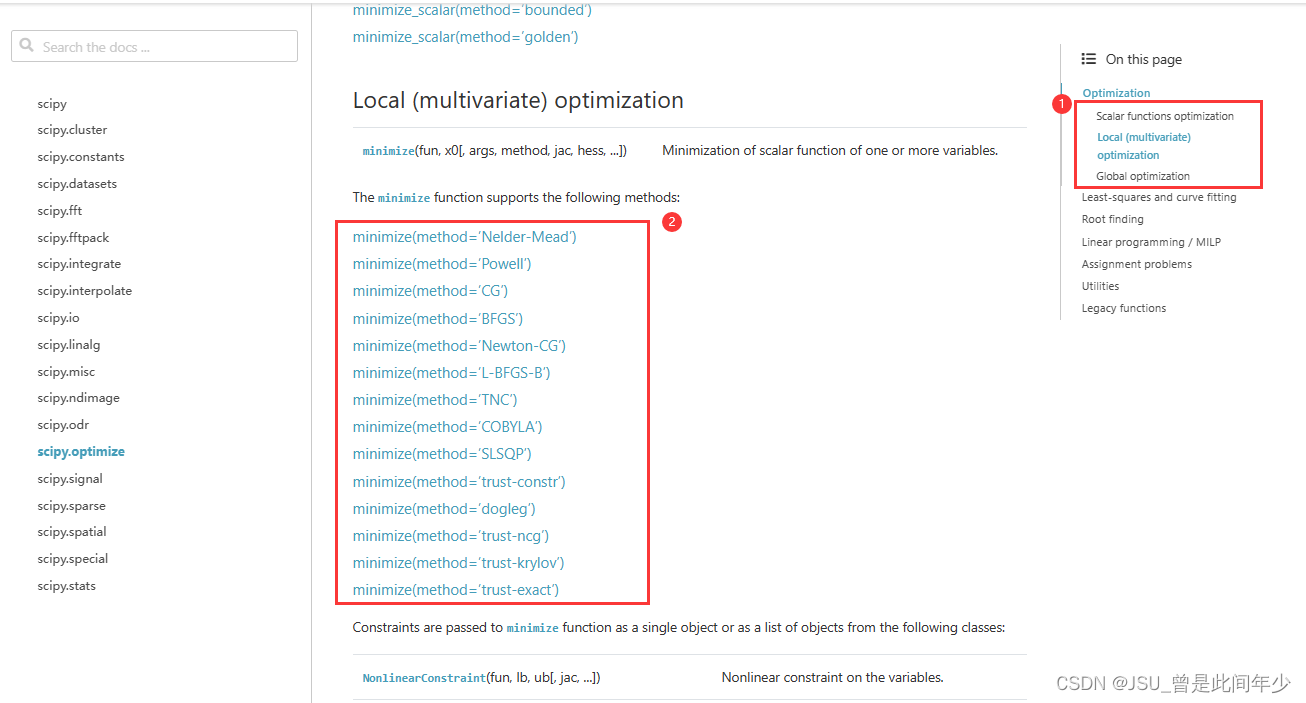
名称特点应用场景
Scalar Functions Optimization用于最小化或最大化单个标量函数的，通常用于解决一维问题目标函数只返回一个标量（单个值）
Local (Multivariate) Optimization适用于多变量问题，需要梯度函数，不过会自动寻找梯度更新目标值在参数空间中找到局部最小值或最大值
Global Optimization寻找函数的全局最小值或最大值，包含多个局部最值在计算条件允许的条件下可以得到全局最优解

优化方法
序号名称使用方法适用条件
1Nelder-MeadNelder-Mead单纯形法适用于一般的非线性问题
2PowellPowell方法适合多维非约束优化的方法
3CG共轭梯度法（Conjugate Gradient）适用于二次优化问题或大规模问题
4BFGS拟牛顿BFGS算法适用于大多数非线性优化问题的常用方法，尤其是当梯度信息可用时
5Newton-CG牛顿共轭梯度法适用于大多数非线性优化问题，但相对于BFGS需要更多的内存
6L-BFGS-B限制内存BFGS算法适用于大规模问题，因为它限制了内存使用
7TNC截断牛顿法适用于大多数非线性优化问题，并且能够处理约束条件
8COBYLA约束优化适用于具有约束条件的问题
9SLSQP顺序最小二乘法适用于具有约束条件的问题，并且能够处理线性和非线性约束
10trust-constr信任区域约束优化方法适用于有约束条件的问题，并且可以处理线性和非线性约束
11dogleg信任域Dogleg方法适用于具有约束条件的问题
12trust-ncg信任区域牛顿共轭梯度法适用于约束优化问题
13trust-krylov信任区域Krylov子空间法适用于约束优化问题
14trust-exact精确信任区域方法适用于约束优化问题

 此问题我们需要求最小值，所以我们采用minimize函数，并选择常用的BFGS策略

3.minimize函数参数及其返回值

原型如下：

scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)

挑五个主要的参数讲

1.fun：需要最小化的目标函数

这个函数应该接受一个输入向量，返回一个标量（单个值），表示损失函数的值。

2.x0：起始参数的初始猜测值

通常是一个数组或列表，表示参数的初始估计。

3.args：传递给目标函数的额外参数的元组

如果目标函数需要额外的参数，可以将它们作为元组传递给args参数。

4.method：选择优化方法的字符串

这是一个可选参数，如果未指定，默认使用'Nelder-Mead'方法。可以选择其他方法，

5.jac：表示目标函数的梯度（导数）的函数

如果提供了梯度函数，通常可以加速优化过程。如果不提供，优化算法会尝试数值估计梯度。

所以我们在优化代码的时候，

可以将 calcLoseFunction函数作为fun，

而k,b两个参数打成列表作为x0，

将XData,YData组成元组传递给arg

method选择BFGS

最后jac选择不写，便于对比两者速度差异

其返回值说明如下

1.x：优化的参数值。这是一个数组，包含找到的最优参数。

2.fun：最小化目标函数的最小值（损失函数的最小值）。

3.success：一个布尔值，表示优化是否成功收敛到最小值。

4.message：一个字符串，描述优化的终止消息。

5.nit：迭代次数，表示优化算法运行的迭代次数。

6.nfev：函数调用次数，表示评估目标函数的次数。

7.njev：梯度计算次数，表示计算目标函数梯度的次数（如果提供了梯度函数）。

8.hess_inv：Hessian矩阵的逆矩阵（如果提供了Hessian信息）。

9.jac：目标函数的梯度值。

4.代码展示

import numpy #发现直接用List就行了
import random
import matplotlib.pyplot as plt
from scipy.optimize import minimize
from commonTools import *
# random.random()
# random.randint(start,stop)
#################全局数据定义区
# 数组大小
listSize=10
# 定义学习率 取尽量小0.001
learningRate=0.0001
#定义初始直线的 斜率k 和 截距b 45° 1单位距离
# 现在设置 k=0.5 检验程序
k,b=0.5,1
initialParams=[k,b]
#定义迭代次数
bfsNums=9999
#################全局数据定义区END
# 生成随机数
def generateRandomInteger(start, end):# [1-100]return random.randint(start, end)# 打印本次随机生成的X,Y 便于快速粘贴复现
def printXYArray(XData,YData):# 打印Xprint("[", ",".join([str(i) for i in XData]), "]")# 打印Yprint("[", ",".join([str(i) for i in YData]), "]")#调用公共模块进行打印 便于快速查看粘贴
def printXYData(XData,YData):loc=locals()printArray(XData,loc)printArray(YData,loc)
# 最小二乘法定义损失函数 并计算
#参考链接：https://blog.csdn.net/zy_505775013/article/details/88683460
# 求最小二乘法的最小值 最终结果应当是在learningRate一定情况下  这个最小的sum
def calcLoseFunction(params,XData,YData):k, b = paramssum=0for i in range(0,listSize):# 使用偏离值的平方进行累和sum+=(YData[i]-(k*XData[i]+b))**2return sum#梯度下降法
def calcGradientCorrection(b, k, XData, YData, learningRate, bfsNums):for i in range(0, bfsNums):sumk, sumb = 0, 0for j in range(0, listSize):# 定义预测值Y'normalNum = k * XData[j] + b# 计算逆梯度累和sumk += -(2 / listSize) * (normalNum - YData[j]) * XData[j]sumb += -(2 / listSize) * (normalNum - YData[j])# 在逆梯度的方向上进行下一步搜索k += learningRate * sumkb += learningRate * sumbreturn k, b# 随机生成横坐标
XData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 随机生成纵坐标
YData=[XData[i]+generateRandomInteger(-10,10) for i in range(listSize) ]
# 纯随机生成 但是可视化效果不直观
# YData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 死值替换区
# XData=testArrayX
# YData=testArrayYprint("初始选取k={},b={}的情况下的损失函数值为sum={}".format(k,b,calcLoseFunction(initialParams,XData,YData)))
# 对k,b进行梯度修正
# k,b=calcGradientCorrection(b,k,XData,YData,learningRate,bfsNums)
#使用Scipy进行求解
result = minimize(calcLoseFunction, initialParams, args=(XData, YData), method='BFGS')
resultk,resultb=result.x
print("修正后：k={},b={},最小损失sum={},最小二乘法损失sums={}".format(resultk,resultb,result.fun,calcLoseFunction([resultk,resultb],XData,YData)))
print("调试数组")
printXYArray(XData,YData)#画图
plt.plot(XData, YData, 'b.')
plt.plot(XData, resultk*numpy.array(XData)+resultb, 'r')
plt.show()
print("END")

5.结果展示

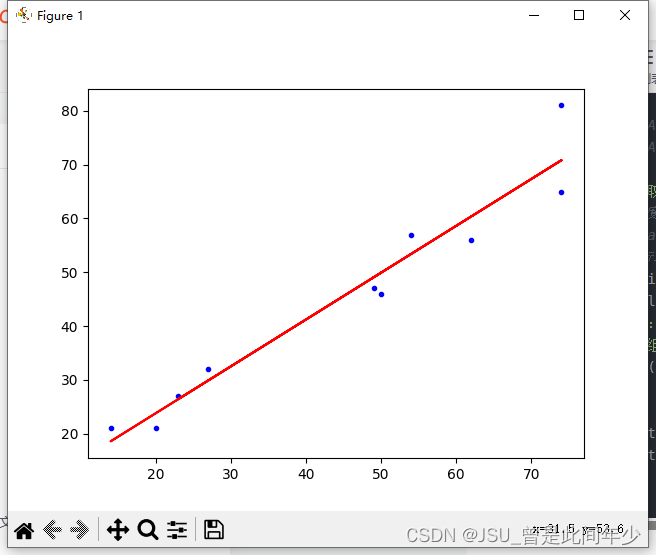
6.进一步优化

两个目标

1.优化损失函数中的for循环

2.对使用Scipy优化前后的代码进行基准测试，比较运行速度

6.1对如下函数方法进行优化
def calcLoseFunction(params,XData,YData):k, b = paramssum=0for i in range(0,listSize):# 使用偏离值的平方进行累和sum+=(YData[i]-(k*XData[i]+b))**2return sum

使用numpy，优化后如下：

def calcLoseFunction(params,XData,YData):XData,YData=np.array(XData),np.array(YData)k, b = paramssum=np.sum((YData - (k * XData + b))**2)return sum

无for优化后代码如下：

import numpy as np
import random
import matplotlib.pyplot as plt
from scipy.optimize import minimize
from commonTools import *#################全局数据定义区
# 数组大小
listSize=10
#定义初始直线的 斜率k 和 截距b 45° 1单位距离
# 现在设置 k=0.5 检验程序
k,b=0.5,1
initialParams=[k,b]
#################全局数据定义区END
# 生成随机数
def generateRandomInteger(start, end):return random.randint(start, end)#调用公共模块进行打印 便于快速查看粘贴
def printXYData(XData,YData):loc=locals()printArray(XData,loc)printArray(YData,loc)# 最小二乘法定义损失函数 并计算
def calcLoseFunction(params,XData,YData):XData,YData=np.array(XData),np.array(YData)k, b = paramssum=np.sum((YData - (k * XData + b))**2)return sum# 随机生成横坐标
XData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 随机生成纵坐标
YData=[XData[i]+generateRandomInteger(-10,10) for i in range(listSize) ]
# 纯随机生成 但是可视化效果不直观
# YData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 死值替换区
# XData=[ 49,74,62,54,20,14,27,74,23,50 ]
# YData=[ 47,65,56,57,21,21,32,81,27,46 ]print("初始选取k={},b={}的情况下的损失函数值为sum={}".format(k,b,calcLoseFunction(initialParams,XData,YData)))#使用Scipy进行求解
result = minimize(calcLoseFunction, initialParams, args=(XData, YData), method='BFGS')
resultk,resultb=result.x
print("修正后：k={},b={},最小损失sum={},最小二乘法损失sums={}".format(resultk,resultb,result.fun,calcLoseFunction([resultk,resultb],XData,YData)))
print("调试数组")
printXYData(XData,YData)#画图
plt.plot(XData, YData, 'b.')
plt.plot(XData, resultk*np.array(XData)+resultb, 'r')
plt.show()
print("END")

其中公共模块commonTools.py 代码如下：

#########导包区#########说明
#1.想要在公共模块区域使用变量列表 必须传进来 因为彼此的变量作用域不同#########公共变量定义区
#这个locals应该是被引入的界面传进来，而不是从这拿
# loc=locals()#########函数书写区
#1.获取变量名称
def getVariableName(variable,loc):for k,v in loc.items():if loc[k] is variable:return k#附带的打印变量名
def printValue(object,loc):print("变量{}的值是{}".format(getVariableName(object,loc),object))# 2.组装列表为字符串
def mergeInSign(dataList,sign):# print(str(sign).join([str(i) for i in dataList]))return str(sign).join([str(i) for i in dataList])# 3.打印一个列表
def printArray(dataArray,loc):print("列表{}的内容是：".format(getVariableName(dataArray,loc)),\"[", ",".join([str(i) for i in dataArray]), "]"\)

原先的代码如下：

import numpy #发现直接用List就行了
import random
import matplotlib.pyplot as plt
# random.random()
# random.randint(start,stop)
#################全局数据定义区
# 数组大小
listSize=10
# 定义学习率 取尽量小0.001
learningRate=0.0001
#定义初始直线的 斜率k 和 截距b 45° 1单位距离
# 现在设置 k=0.5 检验程序
k,b=0.5,1
#定义迭代次数
bfsNums=9999
#################全局数据定义区END
# 生成随机数
def generateRandomInteger(start, end):# [1-100]return random.randint(start, end)# 打印本次随机生成的X,Y 便于快速粘贴复现
def printXYArray(XData,YData):# 打印Xprint("[", ",".join([str(i) for i in XData]), "]")# 打印Yprint("[", ",".join([str(i) for i in YData]), "]")# 最小二乘法定义损失函数 并计算
#参考链接：https://blog.csdn.net/zy_505775013/article/details/88683460
# 求最小二乘法的最小值 最终结果应当是在learningRate一定情况下  这个最小的sum
def calcLoseFunction(k,b,XData,YData):sum=0for i in range(0,listSize):# 使用偏离值的平方进行累和sum+=(YData[i]-(k*XData[i]+b))**2return sum#梯度下降法
def calcGradientCorrection(b, k, XData, YData, learningRate, bfsNums):for i in range(0, bfsNums):sumk, sumb = 0, 0for j in range(0, listSize):# 定义预测值Y'normalNum = k * XData[j] + b# 计算逆梯度累和  注意这里求偏导应当是两倍 不知道为什么写成1了# 求MSE的偏导sumk += -(2 / listSize) * (normalNum - YData[j]) * XData[j]sumb += -(2 / listSize) * (normalNum - YData[j])# 在逆梯度的方向上进行下一步搜索k += learningRate * sumkb += learningRate * sumbreturn k, b# 随机生成横坐标
XData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 随机生成纵坐标
YData=[XData[i]+generateRandomInteger(-10,10) for i in range(listSize) ]
# 纯随机生成 但是可视化效果不直观
# YData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 死值替换区
# XData=testArrayX
# YData=testArrayYprint("初始选取k={},b={}的情况下的损失函数值为sum={}".format(k,b,calcLoseFunction(k,b,XData,YData)))
# 对k,b进行梯度修正
k,b=calcGradientCorrection(b,k,XData,YData,learningRate,bfsNums)
print("修正后：k={},b={},最小损失sum={}".format(k,b,calcLoseFunction(k,b, XData, YData)))
print("调试数组")
printXYArray(XData,YData)#画图
plt.plot(XData, YData, 'b.')
plt.plot(XData, k*numpy.array(XData)+b, 'r')
plt.show()
print("END")

 到此，使用scipy并对for循环进行优化已经完成，下面我们使用程序对比优化后时间效率上有没有改进。

6.2基准测试

我们将先后代码的画图部分都注释

目录结构如下：

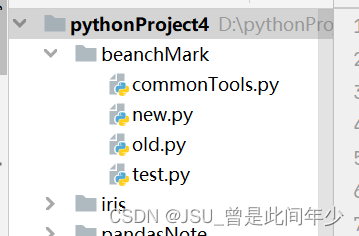
 test.py代码如下：

import os       #执行调用
import time     #记录时间
DEBUG=False
execFileName="old.py" if DEBUG else "new.py"if __name__=="__main__":startTime = time.time()os.system("python {}".format(execFileName))endTime = time.time()print("文件：{}执行耗时：{}ms".format(execFileName,endTime-startTime))

DEBUG为False

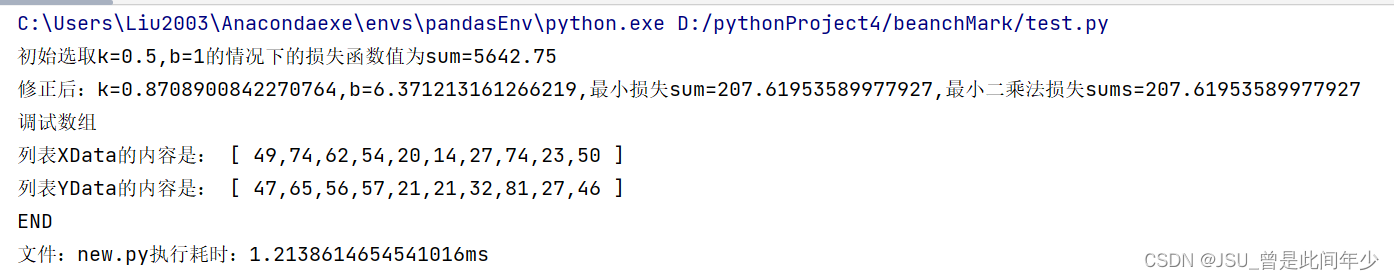
DEBUG为True

额，调用minimize函数在时间上不如自己写的梯度下降。。。。。

多次随机测试后发现结果依旧如此，可能是因为scipy引入了其他策略，导致了执行时间变长

6.3 发现

使用scipy在某种程度上可能能优化执行效率，但是在部分情况下可能耗时会略长于基本实现

测试文件附录

commonTools.py

#########导包区#########说明
#1.想要在公共模块区域使用变量列表 必须传进来 因为彼此的变量作用域不同#########公共变量定义区
#这个locals应该是被引入的界面传进来，而不是从这拿
# loc=locals()#########函数书写区
#1.获取变量名称
def getVariableName(variable,loc):for k,v in loc.items():if loc[k] is variable:return k#附带的打印变量名
def printValue(object,loc):print("变量{}的值是{}".format(getVariableName(object,loc),object))# 2.组装列表为字符串
def mergeInSign(dataList,sign):# print(str(sign).join([str(i) for i in dataList]))return str(sign).join([str(i) for i in dataList])# 3.打印一个列表
def printArray(dataArray,loc):print("列表{}的内容是：".format(getVariableName(dataArray,loc)),\"[", ",".join([str(i) for i in dataArray]), "]"\)

test.py

import os       #执行调用
import time     #记录时间
DEBUG=True
execFileName="old.py" if DEBUG else "new.py"if __name__=="__main__":startTime = time.time()os.system("python {}".format(execFileName))endTime = time.time()print("文件：{}执行耗时：{}ms".format(execFileName,endTime-startTime))

new.py

import numpy as np
import random
import matplotlib.pyplot as plt
from scipy.optimize import minimize
from commonTools import *#################全局数据定义区
# 数组大小
listSize=10
#定义初始直线的 斜率k 和 截距b 45° 1单位距离
# 现在设置 k=0.5 检验程序
k,b=0.5,1
initialParams=[k,b]
#################全局数据定义区END
# 生成随机数
def generateRandomInteger(start, end):return random.randint(start, end)#调用公共模块进行打印 便于快速查看粘贴
def printXYData(XData,YData):loc=locals()printArray(XData,loc)printArray(YData,loc)# 最小二乘法定义损失函数 并计算
def calcLoseFunction(params,XData,YData):XData,YData=np.array(XData),np.array(YData)k, b = paramssum=np.sum((YData - (k * XData + b))**2)return sum# # 随机生成横坐标
# XData=[generateRandomInteger(1,100) for i in range(listSize) ]
# # 随机生成纵坐标
# YData=[XData[i]+generateRandomInteger(-10,10) for i in range(listSize) ]
# 纯随机生成 但是可视化效果不直观
# YData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 死值替换区
XData=[ 49,74,62,54,20,14,27,74,23,50 ]
YData=[ 47,65,56,57,21,21,32,81,27,46 ]print("初始选取k={},b={}的情况下的损失函数值为sum={}".format(k,b,calcLoseFunction(initialParams,XData,YData)))#使用Scipy进行求解
result = minimize(calcLoseFunction, initialParams, args=(XData, YData), method='BFGS')
resultk,resultb=result.x
print("修正后：k={},b={},最小损失sum={},最小二乘法损失sums={}".format(resultk,resultb,result.fun,calcLoseFunction([resultk,resultb],XData,YData)))
print("调试数组")
printXYData(XData,YData)#画图
# plt.plot(XData, YData, 'b.')
# plt.plot(XData, resultk*np.array(XData)+resultb, 'r')
# plt.show()
print("END")

old.py 

import numpy  # 发现直接用List就行了
import random
import matplotlib.pyplot as plt
from commonTools import *
# random.random()
# random.randint(start,stop)
#################全局数据定义区
# 数组大小
listSize = 10
# 定义学习率 取尽量小0.001
learningRate = 0.0001
# 定义初始直线的 斜率k 和 截距b 45° 1单位距离
# 现在设置 k=0.5 检验程序
k, b = 0.5, 1
# 定义迭代次数
bfsNums = 9999#################全局数据定义区END
# 生成随机数
def generateRandomInteger(start, end):# [1-100]return random.randint(start, end)# 打印本次随机生成的X,Y 便于快速粘贴复现
def printXYArray(XData, YData):# 打印Xprint("[", ",".join([str(i) for i in XData]), "]")# 打印Yprint("[", ",".join([str(i) for i in YData]), "]")# 最小二乘法定义损失函数 并计算
# 参考链接：https://blog.csdn.net/zy_505775013/article/details/88683460
# 求最小二乘法的最小值 最终结果应当是在learningRate一定情况下  这个最小的sum
def calcLoseFunction(k, b, XData, YData):sum = 0for i in range(0, listSize):# 使用偏离值的平方进行累和sum += (YData[i] - (k * XData[i] + b)) ** 2return sum# 梯度下降法
def calcGradientCorrection(b, k, XData, YData, learningRate, bfsNums):for i in range(0, bfsNums):sumk, sumb = 0, 0for j in range(0, listSize):# 定义预测值Y'normalNum = k * XData[j] + b# 计算逆梯度累和  注意这里求偏导应当是两倍 不知道为什么写成1了# 求MSE的偏导sumk += -(2 / listSize) * (normalNum - YData[j]) * XData[j]sumb += -(2 / listSize) * (normalNum - YData[j])# 在逆梯度的方向上进行下一步搜索k += learningRate * sumkb += learningRate * sumbreturn k, b# 随机生成横坐标
XData = [generateRandomInteger(1, 100) for i in range(listSize)]
# 随机生成纵坐标
YData = [XData[i] + generateRandomInteger(-10, 10) for i in range(listSize)]
# 纯随机生成 但是可视化效果不直观
# YData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 死值替换区
# XData=[ 49,74,62,54,20,14,27,74,23,50 ]
# YData=[ 47,65,56,57,21,21,32,81,27,46 ]print("初始选取k={},b={}的情况下的损失函数值为sum={}".format(k, b, calcLoseFunction(k, b, XData, YData)))
# 对k,b进行梯度修正
k, b = calcGradientCorrection(b, k, XData, YData, learningRate, bfsNums)
print("修正后：k={},b={},最小损失sum={}".format(k, b, calcLoseFunction(k, b, XData, YData)))
print("调试数组")
printXYArray(XData, YData)# 画图
# plt.plot(XData, YData, 'b.')
# plt.plot(XData, k * numpy.array(XData) + b, 'r')
# plt.show()
print("END")

任务清单

1.算法程序不使用任何for循环（已完成）

2.使用scipy对原先的代码进行优化（已完成）

3.对优化前后代码进行基准测试（已完成）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/149337.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【最新】如何在CSDN个人主页左侧栏添加二维码？侧边推广怎么弄?

【最新】如何在CSDN个人主页左侧栏添加二维码？侧边推广怎么弄?

目录 引言 效果展示 步骤讲解 引言 当你决定在CSDN上展示自己的技术才能和项目时，💡 将你的个人主页变得更炫酷和引人注目是必不可少的！在这篇博客中，我们将向你揭开神秘的面纱，教你如何在CSDN个人主页的左侧栏上添…
阅读更多...
搭建Windows上的Qt桌面开发环境

搭建Windows上的Qt桌面开发环境

搭建Windows上的Qt桌面开发环境 准备有效邮箱安装VS2019 CommunityMicrosoft个人账号注册地址下载在线安装器安装C工具链 安装QtQt开发者账号注册地址下载在线安装器安装Qt 5.15工具链和Qt Creator 使用Qt Creator编译示例工程配置构建套件（Kit）打开示例…
阅读更多...
MySQL进阶-存储引擎

MySQL进阶-存储引擎

目录 1.MySQL体系结构 体系结构图 各层的作用 2.存储引擎简介 2.1查看当前表的存储引擎 2.2 查询mysql支持的存储引擎 2.3 InnoDB简介 2.4 MyISAM简介 2.5 Memory简介 3.存储引擎的选择 1.MySQL体系结构 mysql体系结构主要有四层结构，从上到下依次是&#…
阅读更多...
论文阅读——Pyramid Grafting Network for One-Stage High Resolution Saliency Detection

论文阅读——Pyramid Grafting Network for One-Stage High Resolution Saliency Detection

目录 基本信息标题目前存在的问题改进网络结构CMGM模块解答为什么要用这两个编码器进行编码 另一个写的好的参考 基本信息 期刊CVPR年份2022论文地址https://arxiv.org/pdf/2204.05041.pdf代码地址https://github.com/iCVTEAM/PGNet 标题 金字塔嫁接网络的一级高分辨率显著性…
阅读更多...
Vue3 模糊搜索筛选

Vue3 模糊搜索筛选

Vue3 模糊搜索筛选 环境&#xff1a; vue3 tselement plus 目标&#xff1a; 输入框输入内容&#xff0c;对展示的列表进行模糊搜索筛选匹配的内容。 代码如下&#xff1a; <div style"margin-top: 50px"><el-input v-model"valueInput" size&…
阅读更多...
纸质书籍OCR方案大揭秘，快来看看有哪些神奇的黑科技

纸质书籍OCR方案大揭秘，快来看看有哪些神奇的黑科技

随着数字化时代的来临&#xff0c;纸质书籍逐渐被电子书所替代。在将纸质书籍转换为电子格式的过程中&#xff0c;扫描电子书目录并进行文字识别&#xff08;OCR&#xff0c;Optical Character Recognition&#xff09;成为了一项重要的工作。OCR技术能够将纸质书籍中的文字内容…
阅读更多...
【开发篇】十六、SpringBoot整合JavaMail实现发邮件

【开发篇】十六、SpringBoot整合JavaMail实现发邮件

文章目录 0、相关协议1、SpringBoot整合JavaMail2、发送简单邮件3、发送复杂邮件 0、相关协议 SMTP&#xff08;Simple Mail Transfer Protocol&#xff09;&#xff1a;简单邮件传输协议&#xff0c;用于发送电子邮件的传输协议POP3&#xff08;Post Office Protocol - Versi…
阅读更多...
基于SpringBoot的学生选课系统

基于SpringBoot的学生选课系统

基于SpringBoot的学生选课系统的设计与实现&#xff0c;前后端分离 开发语言&#xff1a;Java数据库&#xff1a;MySQL技术&#xff1a;SpringBootMyBatisVue工具&#xff1a;IDEA/Ecilpse、Navicat、Maven 前台主页 登录界面 管理员界面 教师界面 学生界面 摘要 学生选课系统…
阅读更多...
Electron笔记

Electron笔记

基础环境搭建 官网:https://www.electronjs.org/zh/ 这一套笔记根据这套视频而写的 创建项目 方式一: 官网点击GitHub往下拉找到快速入门就能看到下面这几个命令了 git clone https://github.com/electron/electron-quick-start //克隆项目 cd electron-quick-start //…
阅读更多...
Spring Cloud OpenFeign 性能优化的4个方法

Spring Cloud OpenFeign 性能优化的4个方法

OpenFeign 是 Spring 官方推出的一种声明式服务调用和负载均衡组件。它的出现就是为了替代已经进入停更维护状态的 Netflix Feign&#xff0c;是目前微服务间请求的常用通讯组件。 1.超时设置 OpenFeign 底层依赖Ribbon 框架&#xff0c;并且使用了 Ribbon 的请求连接超时时间…
阅读更多...
使用4090显卡部署 Qwen-14B-Chat-Int4

使用4090显卡部署 Qwen-14B-Chat-Int4

使用4090显卡部署 Qwen-14B-Chat-Int4 1. Qwen-Agent 概述2. Github 地址3. 创建虚拟环境4. 安装依赖项5. 快速使用6. 启动 web 演示7. 访问 Qwen 1. Qwen-Agent 概述 通义千问-14B&#xff08;Qwen-14B&#xff09; 是阿里云研发的通义千问大模型系列的140亿参数规模的模型。…
阅读更多...
【Java】类和接口的区别

【Java】类和接口的区别

1. 类和类的继承关系&#xff08;一个类只能单继承一个父类&#xff0c;不能继承n多个不同的父类&#xff09; 继承关系&#xff0c;只能单继承&#xff0c;但可以多层继承 2. 类和接口的实现关系&#xff08;一个类可以实现n多个不同的接口&#xff09; 实现关系&#xff0c;可…
阅读更多...
从零开始的C++(五)

从零开始的C++(五)

1.类和对象的补充 当对象是const修饰的常量时&#xff0c;形参中的this是隐含的&#xff0c;那么该如何写函数才能传常量对象呢&#xff1f;如果还是按照正常的方式写&#xff0c;则会出现实参是const修饰的&#xff0c;形参没有&#xff0c;出现了权限的扩大&#xff0c;无法…
阅读更多...
开发工具箱 —— it-tools

开发工具箱 —— it-tools

文章目录 开发工具箱 —— it-tools安装访问效果 开发工具箱 —— it-tools 安装 docker 安装教程&#xff1a;在 CentOs7 中安装宝塔面板和 Docker&#xff08;包括MySQL&#xff0c;Redis&#xff09; docker 安装命令 docker run -d --name it-tools --restart unless-st…
阅读更多...
012-第二代硬件选型

012-第二代硬件选型

第二代硬件选型 文章目录 第二代硬件选型项目介绍重新换平台缘由X86 && Arm 架构切换 ARM Linux 硬件选型系统确定Qt 版本确定总结一下 关键字&#xff1a; Qt、 Qml、 Arm、 X86、 linux 项目介绍 欢迎来到我们的 QML & C 项目&#xff01;这个项目结合了 QM…
阅读更多...
浏览器技巧：谷歌浏览器六个实用设置小技巧，值得收藏

浏览器技巧：谷歌浏览器六个实用设置小技巧，值得收藏

目录 1、确保你的浏览器启用标准保护选项 2、使用安全DNS&#xff08;DNS over HTTPS&#xff09; 3、网站通知修改为"静态指示方式" 4、启用页面预加载提升网页加载速度 5、阻止Chrome浏览器在后台运行 6. 更改 Chrome 启动后打开方式为"上次打开的网页&…
阅读更多...
Android---字节码层面分析Class类文件

Android---字节码层面分析Class类文件

Java 提供了一种可以在所有平台上都能使用的一种中间代码---字节码文件(.class文件)。有了字节码&#xff0c;无论是那个平台只要安装了虚拟机都可以直接运行字节码文件。有了虚拟机&#xff0c;解除了 java 虚拟机与 java 代码之间的耦合。 Java 虚拟机当初被设计出来时就不单…
阅读更多...
如何搭建一个 websocket

如何搭建一个 websocket

环境: NodeJssocket.io 4.7.2 安装依赖 yarn add socket.io创建服务器 引入文件 特别注意: 涉及到 colors 的代码&#xff0c;请采取 console.log() 打印 // 基础老三样 import http from "http"; import fs from "fs"; import { Server } from &quo…
阅读更多...
安装NodeJS并使用yarn下载前端依赖

安装NodeJS并使用yarn下载前端依赖

文章目录 1、安装NodeJS1.1 下载NodeJS安装包1.2 解压并配置NodeJS1.3 验证是否安装成功2、使用yarn下载前端依赖2.1 安装yarn2.2 使用yarn下载前端依赖参考目标：在Windows下安装新版NodeJS，并使用yarn下载前端依赖，实现运行前端项目。 1、安装NodeJS 1.1 下载NodeJS安装包…
阅读更多...
面试题：Redis和MySQL的事务区别是什么？

面试题：Redis和MySQL的事务区别是什么？

大家好&#xff0c;我是小米&#xff01;今天我要和大家聊聊一个在技术面试中经常被问到的问题&#xff1a;“Redis和MySQL的事务区别是什么&#xff1f;”这个问题看似简单&#xff0c;但实际上涉及到了数据库和缓存两个不同领域的知识&#xff0c;让我们一起来深入了解一下吧…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023