题目描述
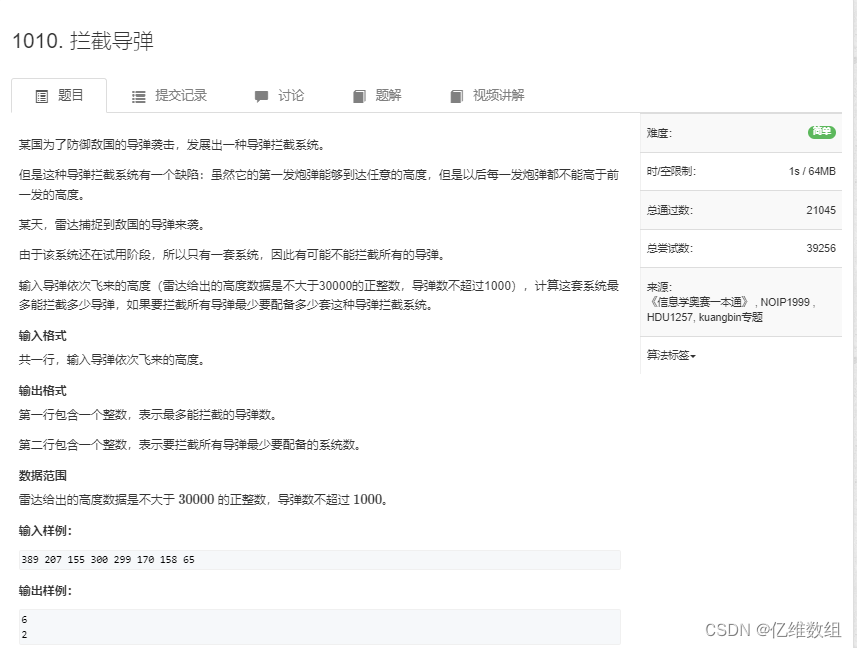
思路分析
本题有两问,第一问直接用lis的模板即可,下面重点看第二问
思路是贪心:
贪心流程:
从前往后扫描每一个数,对于每个数:
情况一:如果现有的子序列的结尾都小于当前的数,则创建子序列
情况二:将当前的数放到结尾大于等于它的最小的子序列后面
举个例子:
360 322 555 222.....
从左到右遍历上面序列,当遍历到222的时候,此时已经存在了两个子序列“360 322”和“555”,两个子序列的结尾分别是322和555,其中322是大于等于222且是“322和555”中最小的数,所以把222放在序列“360 322”的后边!
贪心证明:
A表示贪心算法得到的序列个数,B表示最优解
B<=A 显然
如何证明B>=A?利用调整法:
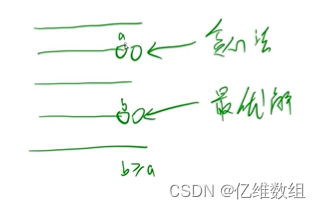
如上图所示,假设a的后面是利用贪心算法插入的一个数,b的后面是最优解插入的一个数
在这两个序列后面补齐之后:
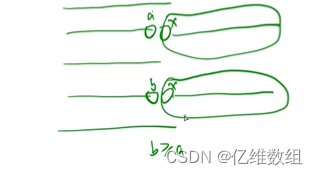
因为a是最优解的插法,所以b>=a
可以把x及后面的序列做交换,导致最优解变成了贪心解,并且总序列个数不变,所以B>=A
完整代码:
#include<iostream>
#include<string>
#include<sstream>
using namespace std;
const int N=1010;
int f[N],h[N],q[N];
int cnt,res;
int n;
int main()
{string str;getline(cin,str);stringstream ssin(str);while(ssin>>q[n])n++;for(int i=0;i<n;i++){f[i]=1;for(int j=0;j<i;j++)if(q[j]>=q[i])f[i]=max(f[j]+1,f[i]);res=max(res,f[i]);int k=0;while(k<cnt&&h[k]<q[i])k++;if(k<cnt)h[k]=q[i];elseh[cnt++]=q[i];}cout<<res<<endl<<cnt<<endl;return 0;
}