详解链表oJ＜反转链表，链表的中间节点及链表的回文＞

在这里插入图片描述

hello，大家好，这里是Dark FlameMaster,今天和大家分享的是有关数据结构链表的几道题目，链表的中间节点，反转链表及判断链表是否为回文结构，放在一起讲解会印象更加深刻。

文章目录

- 一，链表的中间节点
- 二，反转链表
- 三，链表的回文

一，链表的中间节点

链接：链表的中间节点

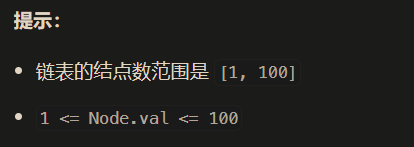
在这里插入图片描述

分析：
如果想要得到链表的中间节点，最简单的思路就是从头结点遍历整个链表，就可以知道链表的长度，假设为num个，要求是如果为偶数个数，返回第二个节点。得到个数后要创建新的节点，往后走num/2个位置。如果num为奇数，如5，往后next两步，如果是偶数如6,往后next3步，皆满足要求。
实现：

struct ListNode* middleNode(struct ListNode* head){struct ListNode* ret = head;int len = 0;int k = 0;while(ret){ret = ret -> next;len++;}ret = head;while(k < len / 2){k++;ret = ret -> next;}return ret;
}

此题还有一种双指针的方法
思路：
设置快慢指针，快指针一次走两步，慢指针一次走一步，还是分偶数和奇数的情况。
如果是奇数的话
在这里插入图片描述
如果是偶数的话

要注意观察fast的最终位置
实现如下

struct ListNode* middleNode(struct ListNode* head) {struct ListNode* val = NULL;struct ListNode* baga = NULL;val = head;baga = head;while (val->next != NULL && val->next->next != NULL){val = val->next->next;baga = baga->next;}if (val->next == NULL){return baga;}else{return baga->next;}
}

二，反转链表

链接：反转链表

这道题的介绍很简单，给定一个链表head，将链表反转过来。就像这样。
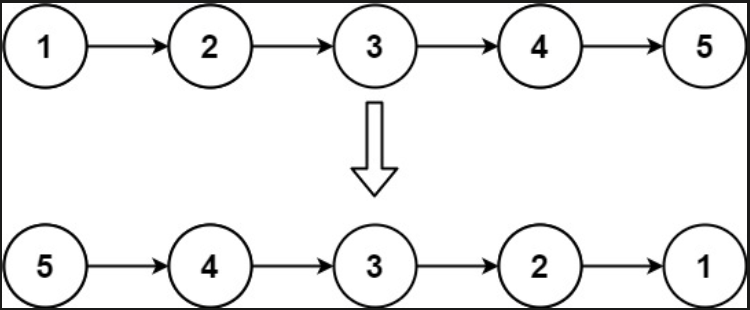
在这里插入图片描述

在这里插入图片描述
需要注意的是，这个链表的长度有可能为零。
思路：
解决这道题，不可冒昧更改一个节点的指向，要记录后续节点，同时还要保留前一个节点，好让这个节点可以指向前一节点，所以要设置三个结构体指针变量，分别表示要修改的节点，要修改节点的前一节点，该节点的后边的节点。
实现

struct ListNode* reverseList(struct ListNode* head){struct ListNode*n1,*n2,*n3;n1=NULL;//设置n1为空n2=head;//n2为head，首先指向空if(n2){n3=n2->next;//判断n2是否为空，若为空则没有next      }while(n2){n2->next=n1;n1=n2;n2=n3;if(n3)//判断n3是否为空{n3=n3->next;}}return n1;
}

下边的动图可以帮助大家理解
在这里插入图片描述
对比代码看完这些动图就可以很清晰的理解。

三，链表的回文

链接：链表的回文
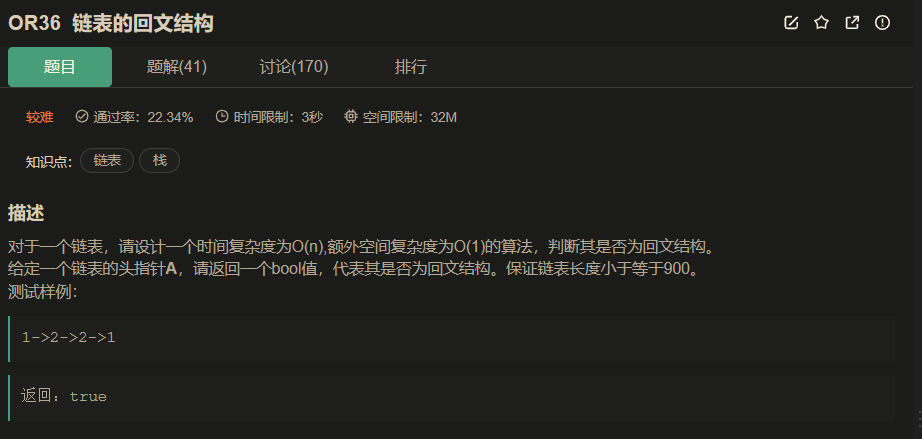
在这里插入图片描述
设计时间复杂度为O(N),空间复杂度为O(1)的算法

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
上边已经说了链表的长度有限制，空间复杂度为O（1）无疑，只要写出的代码中不使用两层以上循环遍历，用有限的多个循环，时间复杂度都为O(1)
判断是否为回文结构
如用例中的1-2-2-1，从中间分割后两边对称。
再如
1-2-3-2-1，仍然为回文结构。

如何判断是否为回文结构呢？好像很难，因为不是双向链表，我们比较的时候找不到尾的前一个，如果硬要一个一个判断的话，时间复杂度一定不符合要求。

如果使用上边的两个题目的思路
上边的找中间节点，刚好为后一个中间节点，找到中间节点后，记录中间节点后，将中间结点之后的链表反转，反转后就可以进行比较了。这也是这三道题放在一起的原因。直接cv，将函数复制过来，判断函数内容十分简单，大家可以对照观察。
思路已经十分清楚了
实现如下：

class PalindromeList {
public:
struct ListNode* middleNode(struct ListNode* head) {struct ListNode* val = NULL;struct ListNode* baga = NULL;val = head;baga = head;while (val->next != NULL && val->next->next != NULL){val = val->next->next;baga = baga->next;}if (val->next == NULL){return baga;}else{return baga->next;}
}
struct ListNode* reverseList(struct ListNode* head){struct ListNode*n1,*n2,*n3;n1=NULL;n2=head;if(n2){n3=n2->next;}while(n2){n2->next=n1;n1=n2;n2=n3;if(n3)//判断n3是否为空n3=n3->next;}return n1;
}bool chkPalindrome(ListNode* A) {// write code herestruct ListNode*mid=middleNode(A);struct ListNode* rmid =reverseList(mid);while(rmid&&A){if(rmid->val!=A->val){return false;}rmid=rmid->next;A=A->next;}return true;}
};