简介
2347DR是一款最大可提供8路ADC接收和8路DAC发射通道的高性能板卡。板卡选用高性价比的Xilinx的Zynq UltraScale+ RFSoC系列中XCZU47DR-FFVE1156作为处理芯片(管脚可以兼容XCZU48DR-FFVE1156,主要差别在有无FEC(信道纠错编解码),其PS端搭配一组4颗16bit的DDR4颗粒,总容量达到4GB;PL端搭配一组2颗16bit的DDR4颗粒,总容量达到2GB。
板载2个Mini USB型式的UART串口分别对应PS和PL端,1个排针式CAN 接口和1个排针式485接口。1个JTAG调试接口,1个DP视频接口,1个千兆网口和2个Type C的USB3.0接口。板载的MMCX连接器最大可提供8路ADC接收和8路DAC发射通道;支持ADC外部差分时钟输入和DAC差分时钟输出;支持外参考时钟、外同步和外触发信号;支持GPS和秒脉冲PPS信号。
板载2个QSFP28形式100Gb高速光纤接口,以及一个M.2型式的SATA接口,一个SD卡和一个多路GPIO对外接口。

应用:
- 雷达、软件无线电等
- FPGA信号处理
- 实时多算法处理的在线测试验证
- 测试测量快速环境搭建
- 高速光纤、采集应用
产品特性:
- FPGA默认为Zynq UltraScale+ RFSoC系列的XCZU47DR-FFVE1156,集成数字上下变频,插值,抽取;
- 兼容XCZU48DR-FFVE1156(支持FEC);
- 板载PS一组4颗共4GB,PL一组2颗共2GB高速DDR4存储器;
- 板载2个256Mb/4bit的SPI Flash组配成一个8bit加载SPI Flash;
- 多种形式的通讯接口,包括JTAG、UART、CAN、485、千兆网口;
- 1个DP视频接口和2个Type C的USB3.0接口;
- 支持最多8路ADC IN和8路DAC OUT,频率接收范围1M~ 6G,发送最大频率6 G。接收器当采用单通道模式时,最大采样率为5Gsps,最大接收通道为8个,正交模式时,接收通道为4个,最大采样率为10Gsps,ADC量化位数为14位。发送器最大采样率为9.85Gsps,八个发送通道,量化位数为14位;
- 支持ADC外部差分时钟输入和DAC差分时钟输出;
- 支持外参考时钟、外同步和外触发信号;
- 支持GPS和秒脉冲PPS信号;
- 支持2个QSFP28形式100Gb高速光纤接口;
- 支持一个M.2型式的SATA接口,一个SD卡;
- 一个包含差分和单端的多路GPIO对外接口;
- 板载温度传感器和风扇转速控制芯片;
- 12V独立电源输入接口,12V直流风扇控制接口;
- 接口指标。
| 模拟输入接口 | |
| 输入频率范围 | 1M~6G |
| 输入最大功率 | 14.6dBm |
| 模拟输出接口 | |
| 输出频率范围 | 0~6G |
| 输出最大功率 | 3 dBm |
| 外部参考时钟输入 | |
| 输入频率频率范围 | 10M~100 M |
| 输入最大功率 | 10 dBm |
| 同步接口 | 支持TTL,LVCMOS |
| 通用接口 | 支持TTL,LVCMOS ,LVDS |
| 秒脉冲接口 | 支持TTL,LVCMOS |
| 外触发 | 支持TTL,LVCMOS |
| GPS接口 | MMCX |
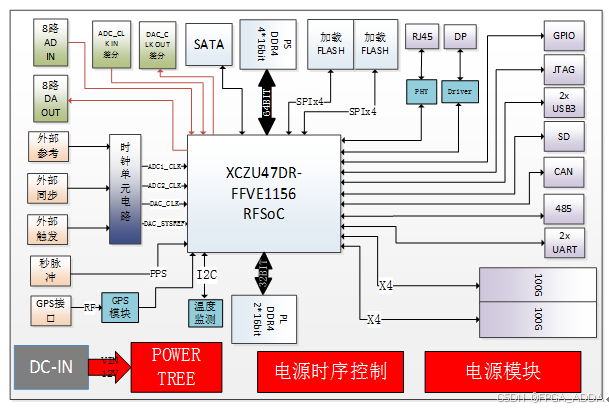
系统主要由时钟管理模块、FPGA控制模块、DDR存储模块、AD/DA模块、接口配置电路模块及电源管理模块组成。其中,时钟管理模块支持外参考、外同步和外触发功能,提供各种功能模块需要的相应时钟信号;FPGA控制模块通过PS向外部提供1路UART、千兆网口、USB3.0、CAN接口、SATA、JTAG、SD、DP等外设接口,PL向外部提供1路UART、485、2路QSFP28等外设接口,可支持各种常用功能的数据交互与控制。
DDR存储模块部分,PS提供一组64bit/4GB的基于DDR4,PL提供一组32bit/2GB的基于DDR4,整板一共6GB的板载存储空间,极大地提高了整个板卡的处理性能和能力。
FPAG集成了数字上下变频,插值,抽取等功能,支持最多8路ADC IN和8路DAC OUT,频率接收范围1M~ 6G,发送最大频率6 G。接收器当采用单通道模式时,最大采样率为5Gsps,最大接收通道为8个,正交模式时,接收通道为4个,最大采样率为5Gsps,ADC量化位数为14位。
发送器最大采样率为9.85Gsps,八个发送通道,量化位数为14位。配置电路模块支持FPGA程序的在线下载和SPI FLASH的烧写,可以方便用户进行实时多算法处理的在线测试验证。
FPGA资源:
Xilinx的Zynq UltraScale+ RFSoC系列芯片均包含PS和PL部分。其中XCZU47DR-FFVE1156管脚可以兼容XCZU48DR-FFVE1156,FFVE1156封装,基本资源几乎一致,主要差别在有无FEC(信道纠错编解码)。如需要FEC(信道纠错编解码)功能,可无缝升级为XCZU48DR-FFVE1156。
其他支持
- 支持 DDR4接口,SATA、DP接口等IP的例程;
- ADC/DAC等成熟功能模块;
- 通用驱动库及开发程序包,支持多种操作系统;
- 可提供部分功能演示程序。