1、效果图实例:

 

 2、部分代码

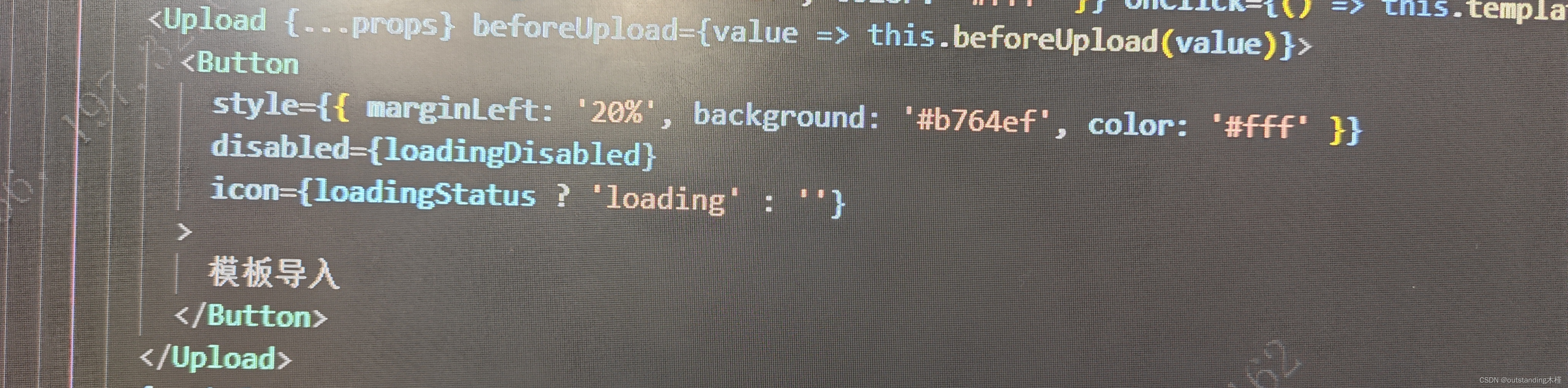
2.1   props :

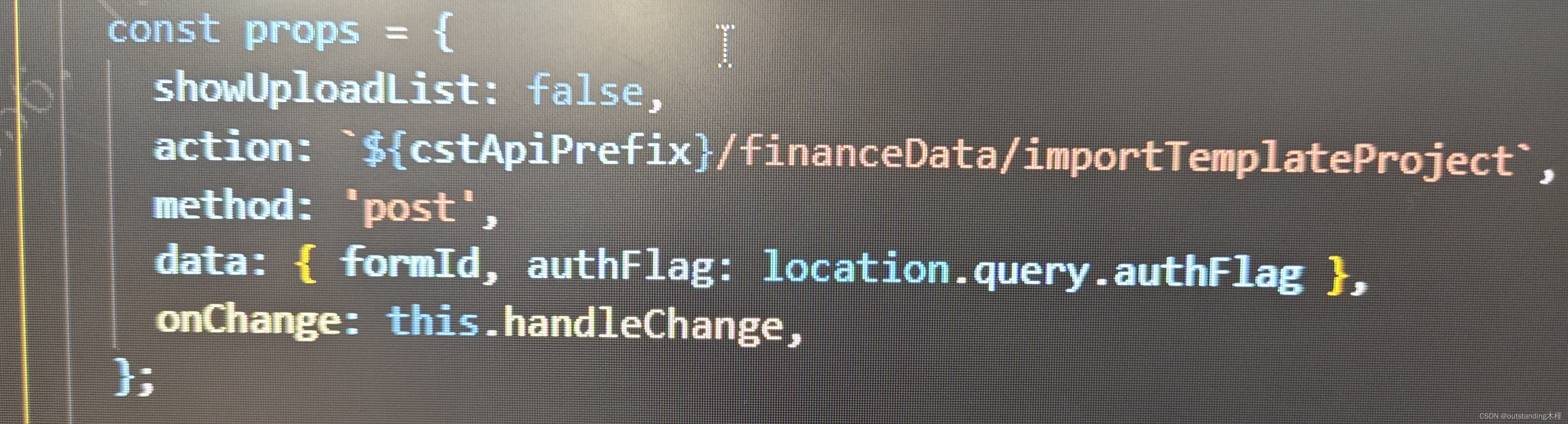
 2.2  handleChange、上传的文件检验 : 

     construction中定义

construction(props) {

    super(props);

    this.state = {

       loadingStaus: flase,

       loadingDisabled: flase, // 作用:按钮如果在加                     载状态中，没上传完，是不可以再次点击上传的

    }

};