语音信号处理之特征提取
语音信号处理之特征提取要对语音信号进行分析,首先要分析并提取出可表示该语音本质的特征参数。有了特征参数才能利用这些特征参数进行有效的处理。
根据提取参数的方法不同,可将语音信号分析分为时域,频域,倒频域,和其他域的分析方法。根据分析方法的不同,可将语音信号分析分为模型分析方法和非模型分析方法。
本文主要以第一种分类方法。时域分析方法简单,计算量小,物理意义明确,但由于语音信号最最重要的感知特性在功率谱中,而人耳对相位变化并不敏感,所以频域分析更为重要。
通过最基本的特征,后面针对不同的任务演变出了各种特征。
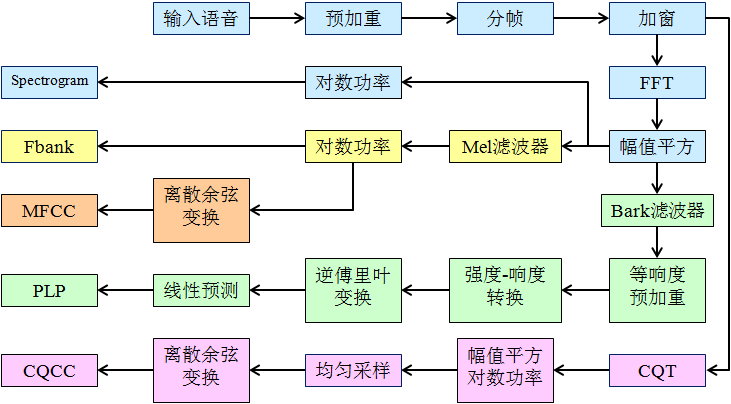
预处理
时域图就是语音波形,横轴时间,纵轴幅值,下是用Adobe Audition打开的音频的波形图,表示这段语音波形时采样率16000Hz,量化精度是16bit。
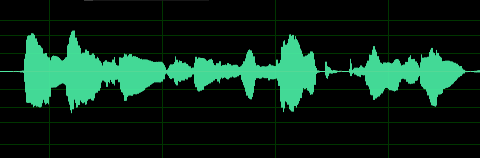
从图中可以得到各个音的起始位置,但很难看出更加有用的信息。但如果我们将其放大到100ms的场景下,可以得到下图所示。
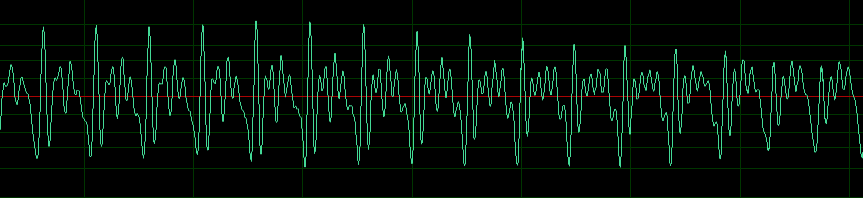
可以看出在短时内波形是存在一定的周期的,不同的发音往往对应着不同的周期的变化,因此在短时域上我们可以将波形通过傅里叶变换转化为频域图,观察音频的周期特性,从而获取有用的音频特征。
额外补充(不感兴趣可跳过)
截取一段清音/s/:确实好像没有周期性规律
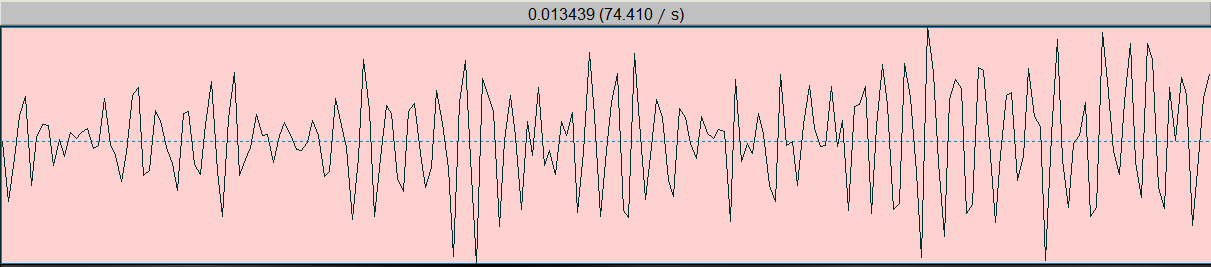
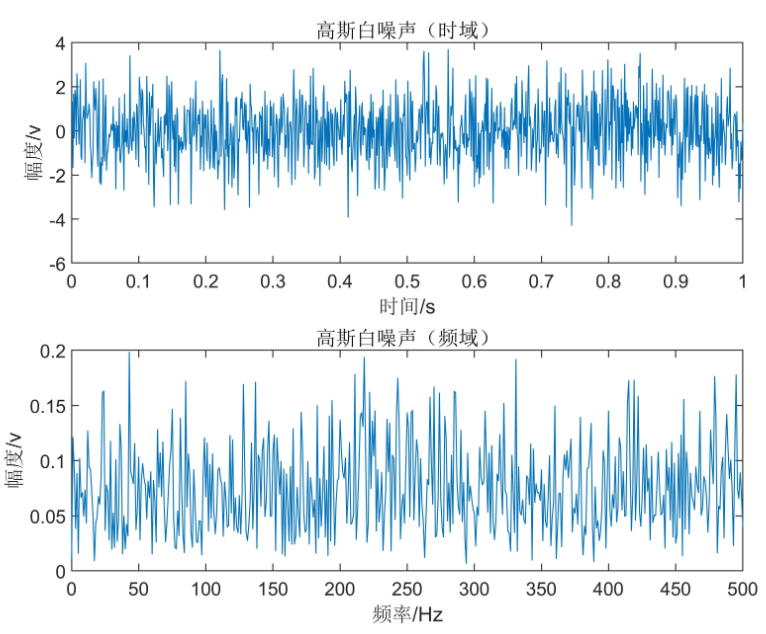
清音一般用白噪声建模:
白噪声(white noise)是指功率谱密度在整个频域内是常数的噪声。 所有频率具有相同能量密度的随机噪声称为白噪声。
再截取一段浊音/o/:短时内波形是存在一定的周期的
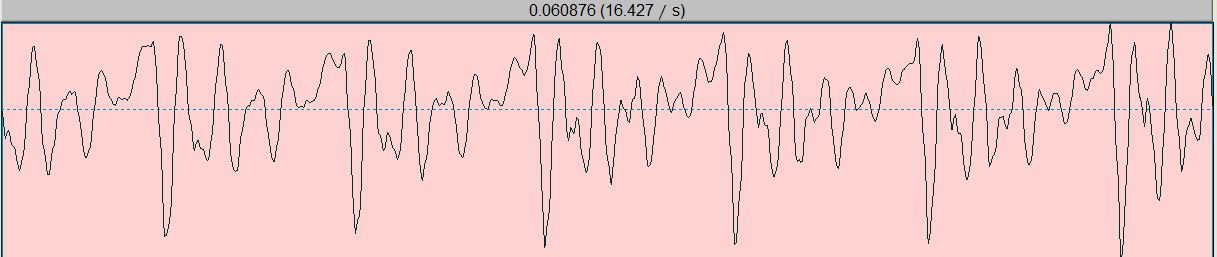
1. 分帧
为什么要分帧?
语音信号是非线性,非平稳,时变的随机信号。但短时内可看作是平稳时不变的,这样就有了分帧技术。
由于语音信号具有短时平稳性,我们通常对语音进行分帧加窗处理,截取短时音频片段,通常帧移的大小为5-10ms,窗长大小通常为帧移的2-3倍即20-30ms。
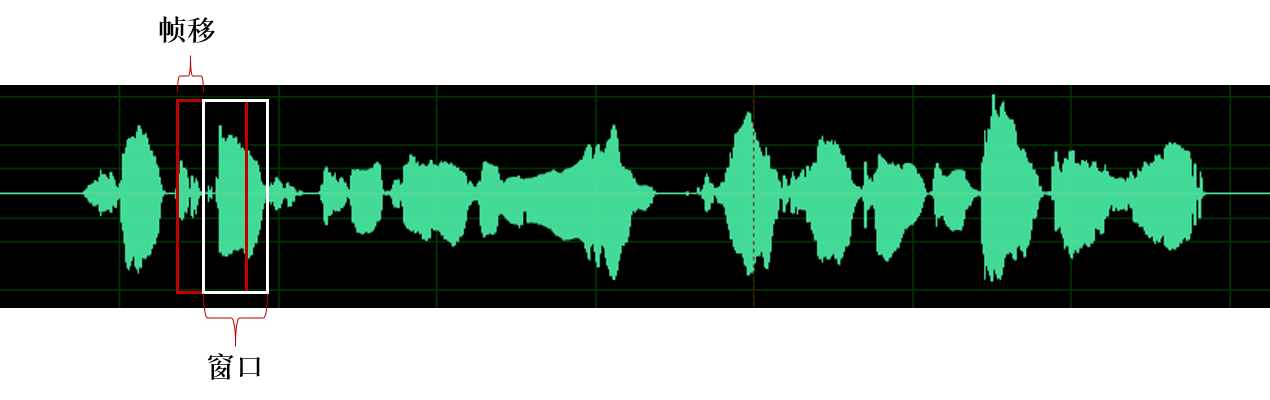
帧长设置有什么依据呢?
从宏观上看,它必须足够短来保证帧内信号是平稳时不变的。口型的变化是导致信号不平稳的原因,所以在一帧的期间内口型不能有明显变化,即一帧的长度应当小于一个音素的长度。正常语速下,音素的持续时间大约是 50~200 毫秒,所以帧长一般取为小于 50 毫秒。
从微观上来看,它又必须包括足够的振动周期,即包含若干个语音的基频,男声基频在 100 Hz左右,女声在 200Hz左右,换算成周期就是 10 ms和 5 ms,所以一般取至少 20 ms。
2. 加窗
为什么要加窗?
加窗的目的有两个:频谱泄露和栅栏效应。
即使语音短时内是准周期的,但分帧时很难保证每帧内就是完全周期的。非周期信号被截断后,经过傅里叶变换FFT,会出现原本信号并没有的频率,即多余的频率成分,这种现象叫做频谱泄露。通过加上合适的窗,可以抑制这些成分,即高次谐波,使得结果更圆滑一些。
对信号做FFT时,得到的是一系列离散的谱线,如果信号中的频率成分位于谱线之间,而不是谱线上,那么就会造成幅值和香味上的偏差,这就是栅栏效应。
理论上,这两种误差都无法消除,但可以选择适合的窗函数进行抑制。
为什么要重叠帧移?
加窗的代价是一帧信号两端的部分被削弱了,没有像中央的部分那样得到重视。弥补的办法是,帧不要背靠背地截取,而是相互重叠一部分。相邻两帧的起始位置的时间差叫做帧移。
加窗操作如下图所示:

一般为矩形窗或汉明窗。
定义矩形窗为w(m):
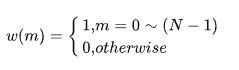
那么对于语音信号 x(t),其加窗分帧后第n帧语音信号 xn(m)为:
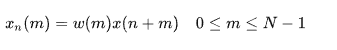
在该计算式中,n=0,T,2T,…,N为帧长,T为帧移长度。
加窗分帧总体:
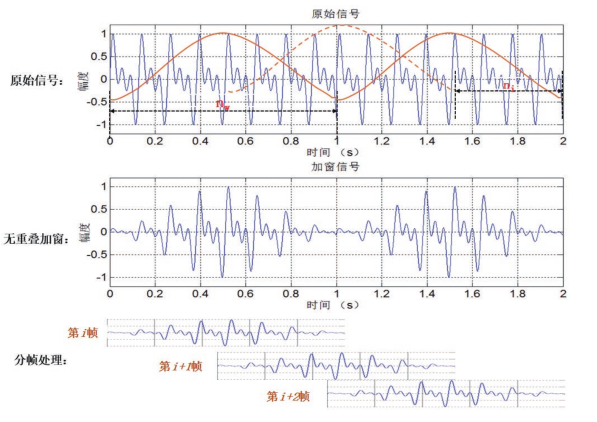
时域特征
1.短时能量、短时平均幅度
第n 帧语音信号 xn(m)的短时能量En为:
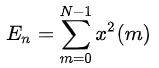
使用幅值平方将对高幅值信号具有较大的敏感度,为了降低敏感度,定义短时平均幅度函数Mn为:
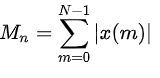
短时能量En和短时平均幅度函数Mn的用途:
-
区分浊音和清音。浊音相比较于清音的En具有较大的数值,因而可用于区分浊音和清音。
-
区分有声段和无声段,也可对声母和韵母分界,对无间隙的连字分界。
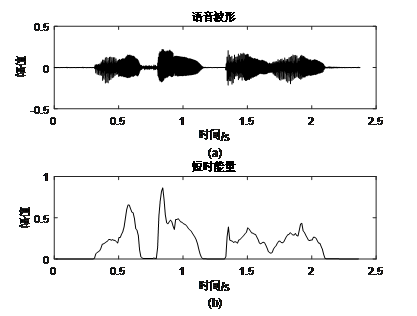
例:语音“蓝天白云”
-
在语音识别任务中作为特征,表示能量特征和超音频信息。
2. 短时过零率
短时过零率表示一帧语音中波形信号穿过零值的次数。对于连续信号,过零意味着波形通过时间轴,而对于离散信号,过零意味着相邻采样点的符号改变。
首先定义符号函数sgn[·]为:
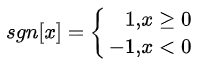
则第n帧语音信号 xn(m)的短时过零率Zn为:
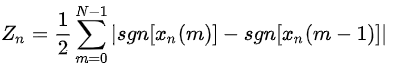
由于短时过零率容易受到低频干扰,可设置相关门限T,将过零修改为穿过正负门限的次数,即:
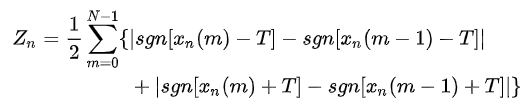
门限的存在使得短时过零率Zn具有一定的扛干扰能力,避免随机噪声导致的虚假过零。
短时过零率的用途:
-
浊音能量集中于3kHz内的低频率段,清音能量集中于高频率段,而短时过零率可以一定程度反映频率高低,因而浊音段相对于清音段,其短时过零率减低。
-
将短时过零率和短时能量结合实现端点检查。短时能量适用于背景噪声较小的情况,而短时过零率适用于背景噪声较大的情况。实际中,通常结合两个参数实现语音起点和终点的判断。
语音“我回来了”
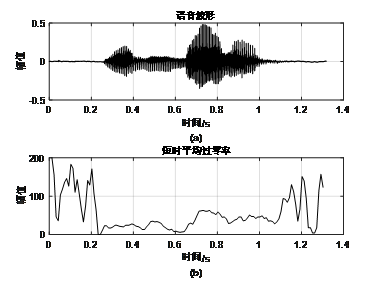
3.短时自相关函数
语音信号xn(m)的短时自相关函数Rn(k)为:
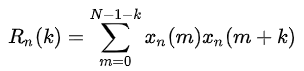
其中,若信号xn(m)具有周期性,则短时自相关函数Rn(k)也具有周期性,且两者周期相同;Rn(k)为偶函数,当k=0时,自相关函数具有最大值。
假设语音信号xn(m)的周期为T,那么短时自相关函数Rn(k)将在k=T,2T…取值时出现峰值。若要出现第一个峰值(即k=T),根据下式:
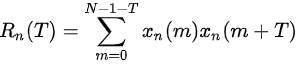
需要取到信号中x(m=2T的样本点,即语音帧宽至少应大于两个周期,否则第一个峰值将无法较好的显示。例语音最小基频为80Hz,最大周期为12.5ms,两倍周期为25ms,因此10kHz的采样信号的帧宽至少为250个采样点。
另一方面,考虑到语音信号的短时性,应设置较低的帧长,因此可使用修正短时自相关函数,其定义为:
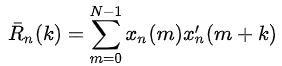
注意:
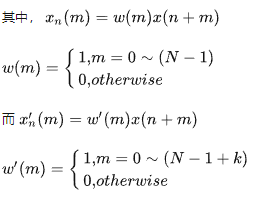
相比于短时自相关函数Rn(k),在修正短时自相关函数中,第一项xn(m)与Rn(k)中的xn(m)相同,而第二项x’n(m)与Rn(k)中的xn(m)相比,差异在于额外向后包括了k个样本点。
在严格定义中,修正短时自相关函数是一个互相关函数,其不满足自相关函数的性质(偶函数性),但其仍在周期整数倍上具有峰值。
短时自相关函数的用途:
- 浊音的自相关函数具有周期性,而清音的自相关函数类似于高频白噪声,没有周期性。
- 根据自相关函数的第一个峰值的位置,估算浊音的基音频率。
4.短时平均幅度差函数
短时自相关函数使用大量乘法运算,计算时间较长,短时平均幅度差Fn(k)使用减法代替了乘法,大大减少了运算量,大量运用于实时语音处理方案上,其定义为:
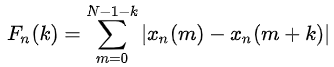
对于周期为T的语音信号,短时平均幅度差Fn(k)在k=T,2T…等取值上具有周期性的极小值。类似的,修正短时平均幅度差为:
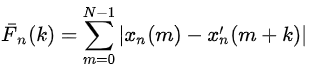
短时平均幅度差Fn(k)和Rn(k)具有数值关系:
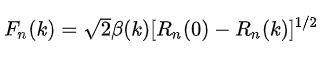
其中,β(k)对不同的语音段,其数值在0.6-1.0之间变化。
短时平均幅度差的用途:
- 基音周期的检测,该方法比短时自相关方法的计算更为简单。
频域特征
1.短时傅里叶变换
短时傅里叶变换(STFT)是最经典的时频域分析方法。所谓短时傅里叶变换,顾名思义,是对短时的信号做傅里叶变化。由于语音波形只有在短时域上才呈现一定周期性,因此使用的短时傅里叶变换可以更为准确的观察语音在频域上的变化。傅里叶变化实现的示意图如下:

一般实现都用快速傅里叶变化FFT。
这里音频经过快速傅里叶变换返回的是复数,其中实部表示的频率的振幅,虚部表示的是频率的相位。
包含FFT函数的库有很多,简单列举几个:
import librosa
import torch
import scipyx_stft = librosa.stft(wav, n_fft=fft_size, hop_length=hop_size,win_length=win_length)
x_stft = torch.stft(wav, n_fft=fft_size, hop_length=hop_size, win_length=win_size)
x_stft = scipy.fftpack.fft(wav)
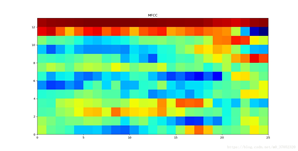
2.语谱图
也叫声谱图,就是声音的可视化图。先将语音信号作FFT,然后以横轴为时间,纵轴为频率,用颜色表示幅值即可绘制出语谱图。在一幅图中表示信号的频率、幅度随时间的变化,故也称“时频图”。
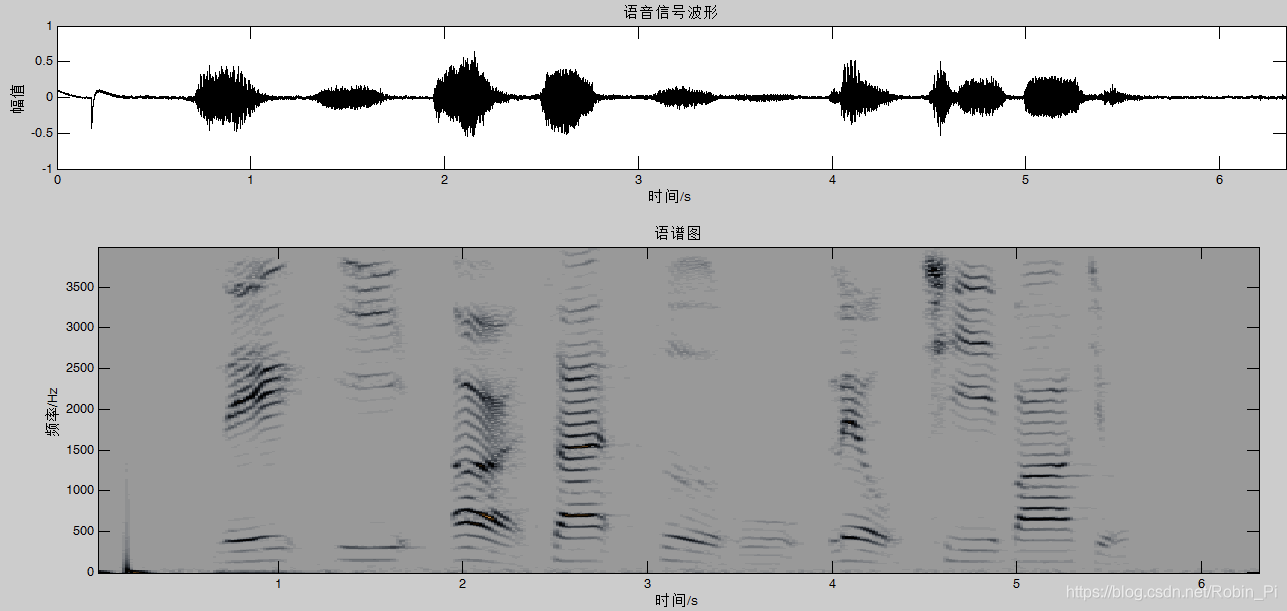
详细原理看我博客:声谱图原理
3. 短时功率谱密度
信号经过FFT得到了频谱,而要反映信号的功率就要求信号的功率谱密度PSD。
功率谱定义:
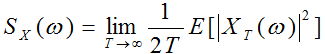
可见对于有限的信号,功率谱之所以可以估计,是基于两点假设:1)信号平稳; 2)随机信号具有遍历性。
相关函数与功率谱密度是互为傅里叶变换。