📙作者简介: 清水加冰,目前大二在读,正在学习C/C++、Python、操作系统、数据库等。
📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。
欢迎点赞 👍 收藏 ⭐留言 📝 如有错误还望各路大佬指正!
✨每一次努力都是一种收获,每一次坚持都是一种成长✨

目录
前言
1. 归并排序
1.1 原理
2. 排序实现
2.1 递归
2.2 非递归
3. 复杂度
空间复杂度
时间复杂度
总结
前言
归并排序也是常用排序算法中较为重要的,对于新手来说较为复杂的排序算法,也是一个十分高效的排序算法。本篇文章我将带领大家深入理解归并排序。
1. 归并排序
归并排序是一种分治算法,它将一个大问题分解成多个小问题,然后将这些小问题的解合并起来得到最终的解。
1.1 原理
- 将待排序的数组分成多个子数组,分别对这些子数组进行归并排序。
- 对有序的两个子数组进行合并,合并后的数组是有序的。
归并排序核心步骤如下:

2. 排序实现
两两合并的前提是两个数组都必须有序,在归并排序中也存在使用递归和非递归的方法实现。
2.1 递归
我们先使用递归来实现归并,归并的过程中我们并不是在原数组中进行排序,我们需要额外创建一个等大的数组,将分解后排序过的数组放到新数组中,然后将新数组中排好的数据拷贝到原数组中。(每合并一次就拷贝一次)
首先我们肯定需要先开辟一个新的数组,然后是对数组进行分讲合并。
void MergrSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}//调整排序接口free(tmp);
}调整排序接口的实现,归并排序是对数组进行二等分,当分解到只有一个数据时开始合并。所以这里使用递归是非常合适的,先分解,当分解到最小,然后开始逐层返回合并(向下递归的过程为分解,递归返回的过程为合并)。
void _MergrSort(int* a, int* tmp, int begin, int end)
{if (end <= begin)return;int mid = (begin + end) / 2;_MergrSort(a, tmp, begin, mid);_MergrSort(a, tmp, mid + 1, end);//归并// ……}接下来就是合并过程的实现。我们已知数组大小,对数组进行不断二分,每次归并时都是两两归并,这里我们需要记录一些两个数组的起始下标。然后遍历两数组,谁小就把数据尾插到新数组。
注意一个数组遍历结束,另一个数组没有结束的情况。
代码如下:
void _MergrSort(int* a, int* tmp, int begin, int end)
{if (end <= begin)return;int mid = (begin + end) / 2;_MergrSort(a, tmp, begin, mid);_MergrSort(a, tmp, mid + 1, end);//合并int begin1 = begin, end1 = mid;//记录两数组的起始下标int begin2 = mid + 1, end2 = end;int index = begin; //记录新数组数据的下标while (begin1 <= end1 && begin2 <= end2)//遍历数组,当一个数组遍历结束就结束{if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}//一共数组结束另一个数组没结束的情况while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}//归并一次,把数据拷贝回原数组一次memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));}注意:记录新数组的下标index不要初始等于0,因为它将合并的数据放到到新数组时,开始的位置不一定是0,index是在函数内创建的变量出函数作用域无法保存,但是它开始的位置恰好就是当前合并范围中数组1的起始位置下标(begin1),所以index=begin;
2.2 非递归
使用递归需要消耗计算机的栈区,而栈区在计算机内存中空间很小,在多次调用函数的过程速度也没有同等条件下循环快(随着计算机的不断完善和优化它们之间差距其实也没那么大),考虑到空间和速度问题,我们很有必要学习一下非递归的实现方法。
非递归相对于递归来说有很多的坑,也更复杂一点。那我们实现非递归要怎么去设计?归并不和快排一样,它使用栈并不能模拟出归并的过程。
为什么?
例如上述的数组,我们在分的时候可以分为以下区间:
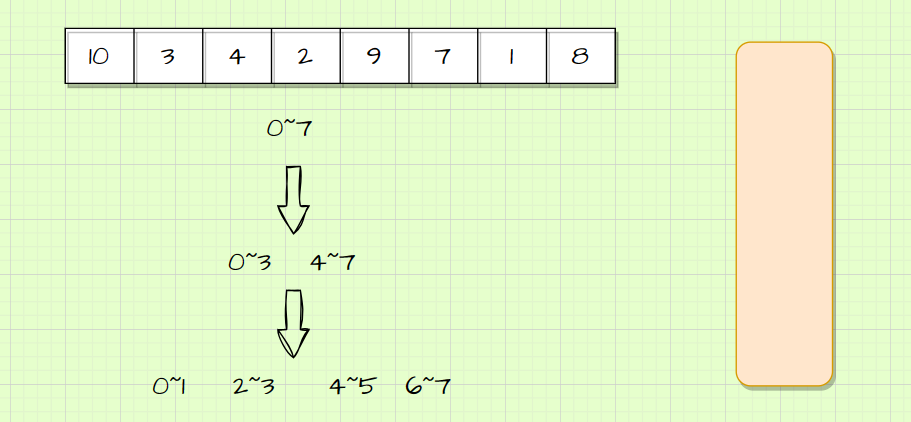
用栈来模拟实现逻辑如下:
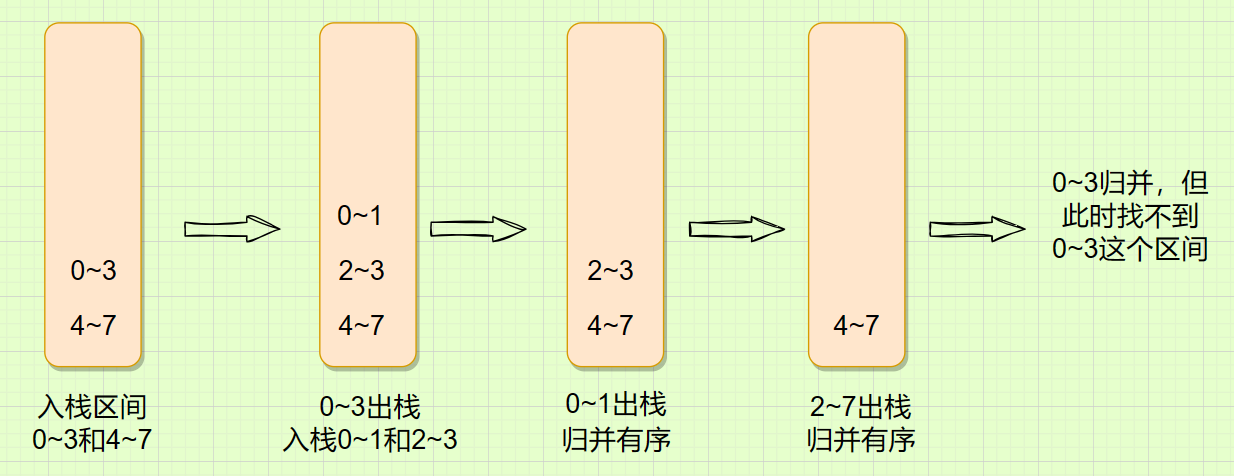
在0~1和2~3区间数据各自归并后拷贝回原数组,下一步就需要将0~1和2~3这两个区间数据归并成一个数组,归并区间是0~3,但此时就再从栈里取,取出的是4~7这个区间。所以使用栈来模拟归并行不通。
那我们要怎么设计?我们来看一下它的归并划分:
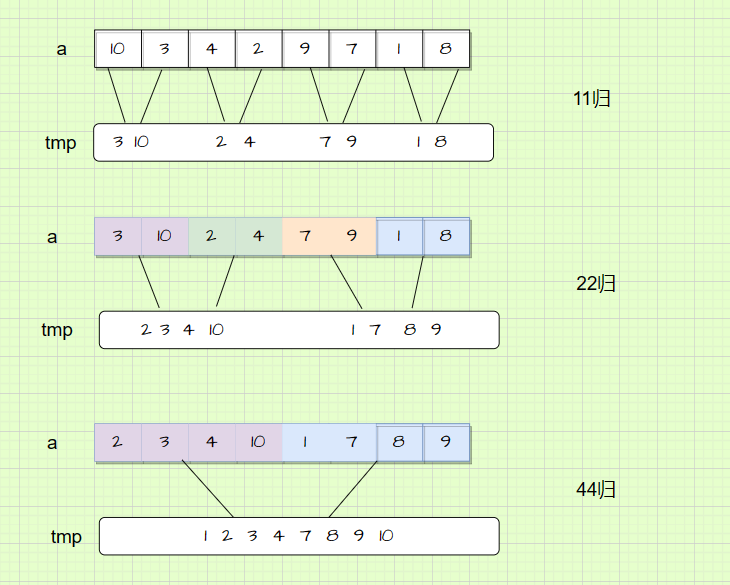
那它的区间变化规律就可以这样写:
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;这里我们可以使用循环来跳区间,i的初始值为0,11归,跳到下一个归并区间开始位置需要跳2步;22归,跳到下一个归并区间开始位置需要跳4步;由此我们找到i的变化规律,i每次增加2倍gap。
void MergrSortNoneR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;for (int i = 0; i < n; i += gap * 2){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int index = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}free(tmp);
}这里的gap默认的是1,前边要求的gap是变化的,11归每次跳到下一个区间开始gap=1,22归每次跳到下一个区间开始gap=2,44归每次跳到下一个区间开始gap=4。gap每次扩大两倍。所以我们还需要再套一个循环:
void MergrSortNoneR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i += gap * 2){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int index = i;//归并//……}gap *= 2;}free(tmp);
}到这里还并没有结束,这个代码还有一个大坑,我们使用的示例是8个数据,那如果是9个数据要怎么办?到第9个数据归并时发现没有和它相对于的归并区间,i如果在一次跳2倍gap就越界了。
注意: 我们在使用递归实现时使用的是除来二分区间,除到最后最小也是0,但使用i跳区间就不一样,它是乘,那就一定存在跳越界的情况。
所以在进行合并之前,我们需要判断一下是否越界,如果越界要及时修正。
for (int i = 0; i < n; i += gap * 2)
{int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int index = i;if (begin2 >= n)//只有一个完整数组{break;}if (end2 >= n)//有一个完整的区间,第二个归并区间超了就修正{end2 = n - 1;//n-1是数组最后元素下标}//归并//……}非递归完整代码如下:
void MergrSortNoneR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i += gap * 2){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int index = i;if (begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}gap *= 2;}free(tmp);
}3. 复杂度
说到排序那就一定要聊一聊它的复杂度。
空间复杂度
在进行排序时我们额外开辟了一个新的等大数组,由此看来它的空间复杂度是O(N)。
时间复杂度
在归并的过程中需要遍历每个子数组,然后重新排序,遍历子数组的时间复杂度是O(N),原数组二分成子数组,一共可以分logN个数组,所以它的时间复杂度就是O(N*logN)。
总结
以上便是本期全部内容,归并排序是一种高效的排序算法,在实际应用中也有很大的价值,是一种值得掌握的算法,希望本文对你有所帮助。最后,感谢阅读!