目录

1 横向交叉操作

2 纵向交叉操作

3 非线性惯性权重

4 基于t分布变异

5 实验结果

---

1 横向交叉操作

       横向交叉操作类似于遗传算法中的交叉操作，是在不同 种群的相同维度中进行交叉运算。针对麻雀搜索算法全局 搜索能力不强的问题，本文应用横向交叉策略对警戒者的位 置进行更新。首先将父代个体随机配对，在第d维进行交叉操作，如下所示：

2 纵向交叉操作

       麻雀搜索算法在后期容易陷入局部最优，在很大程度上 是由于种群中某些个体在某一维度上陷入局部最优，从而使整体过早收敛。经过分析发现，在麻雀搜索算法中缺乏一定的变异机制，无法对已经陷入局部最优个体进行控制，从而阻断了搜索进程和找到全局最优解的可能性。因此，在执行横向交叉操作之后，需要对新生个体进行纵向交叉操作，提高算法规避局部最优的能力。不同于横向交叉操作，纵向交叉操作是在新生个体的所有维度进行的交叉运算，发生的概率小于横向交叉操作，类似于遗传算法中的变异操作。

3 非线性惯性权重

        探索和开发之间的平衡是影响元启发式算法的关键因素。在麻雀搜索算法中，原算法中缺乏对于步长的有效控制，在发现最优解后，其他个体迅速向最优解靠拢，使得算法 难以有效控制全局探索和局部开发进程，从而陷入局部最 优。为此，引入非线性惯性权重ω控制搜索范围和收敛速度。惯性权重ω计算方式如下所示：

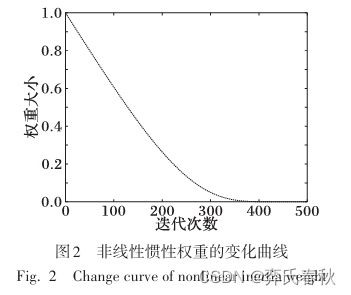
4 基于t分布变异

t分布变异，并进行贪婪选择，保留优秀值。

5 实验结果

       在基准测试函数上进行实验，将ISSA与SSA、ASFSSA、GWO、GJO进行对比，ISSA收敛精度有较大提升。

F1：

The best optimal value of the objective funciton found by SSA is : 8.9979e-82
The best optimal value of the objective funciton found by ISSA is : 0
The best optimal value of the objective funciton found by ASFSSA is : 0
The best optimal value of the objective funciton found by GJO is : 6.1314e-55
The best optimal value of the objective funciton found by GWO is : 1.7217e-27

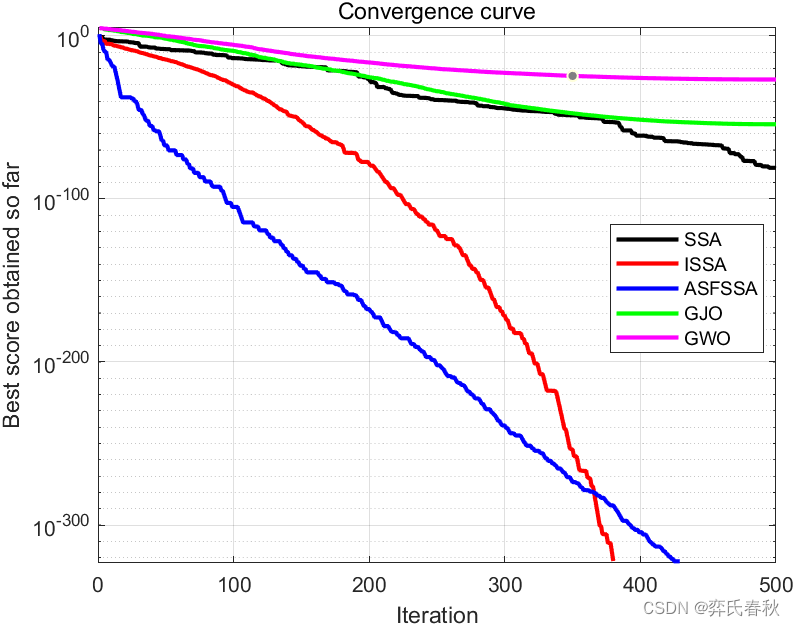
F2:

The best optimal value of the objective funciton found by SSA is : 6.9395e-39
The best optimal value of the objective funciton found by ISSA is : 0
The best optimal value of the objective funciton found by ASFSSA is : 4.76e-191
The best optimal value of the objective funciton found by GJO is : 2.0322e-63
The best optimal value of the objective funciton found by GWO is : 3.6848e-33

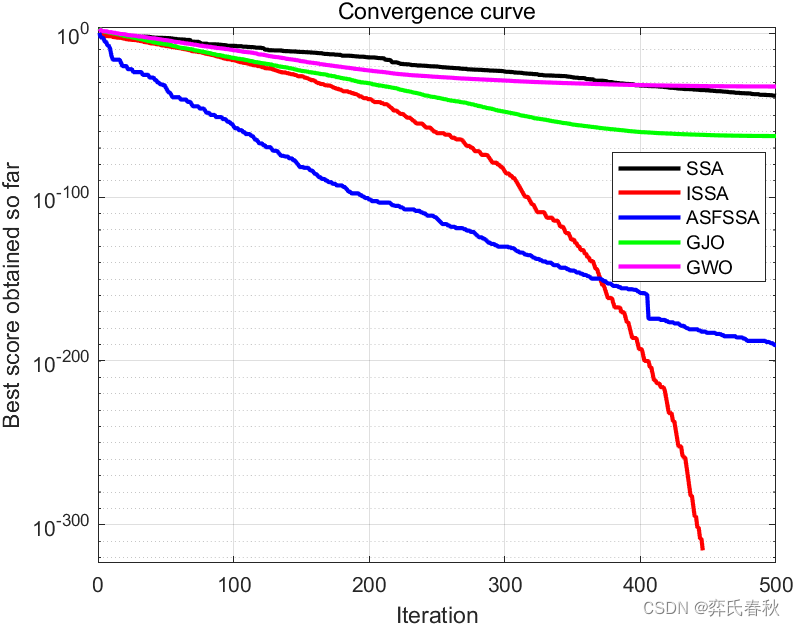
F5:

The best optimal value of the objective funciton found by SSA is : 8.8348e-06
The best optimal value of the objective funciton found by ISSA is : 0
The best optimal value of the objective funciton found by ASFSSA is : 4.7176e-05
The best optimal value of the objective funciton found by GJO is : 8.0757
The best optimal value of the objective funciton found by GWO is : 6.1205 

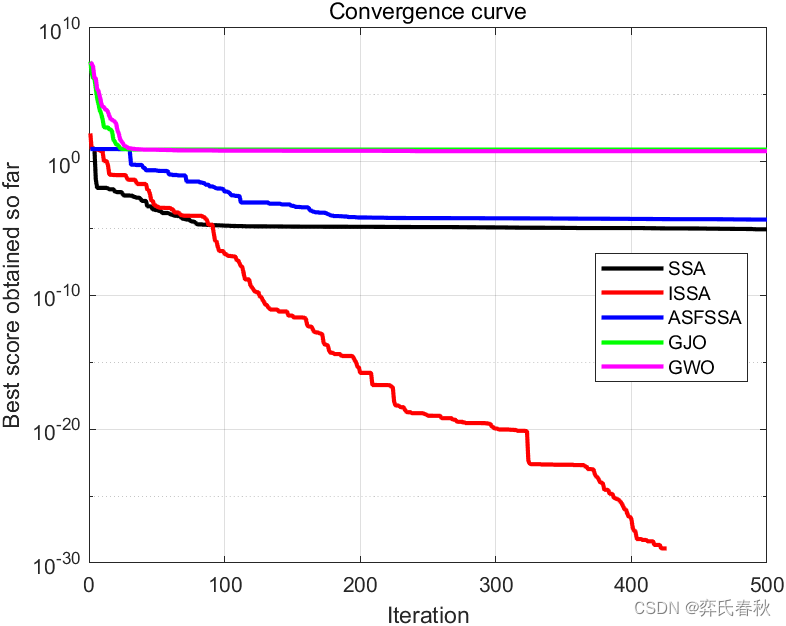
F7:

The best optimal value of the objective funciton found by SSA is : 0.00045455
The best optimal value of the objective funciton found by ISSA is : 9.7154e-05
The best optimal value of the objective funciton found by ASFSSA is : 0.00016112
The best optimal value of the objective funciton found by GJO is : 0.00099729
The best optimal value of the objective funciton found by GWO is : 0.0010465

F9:

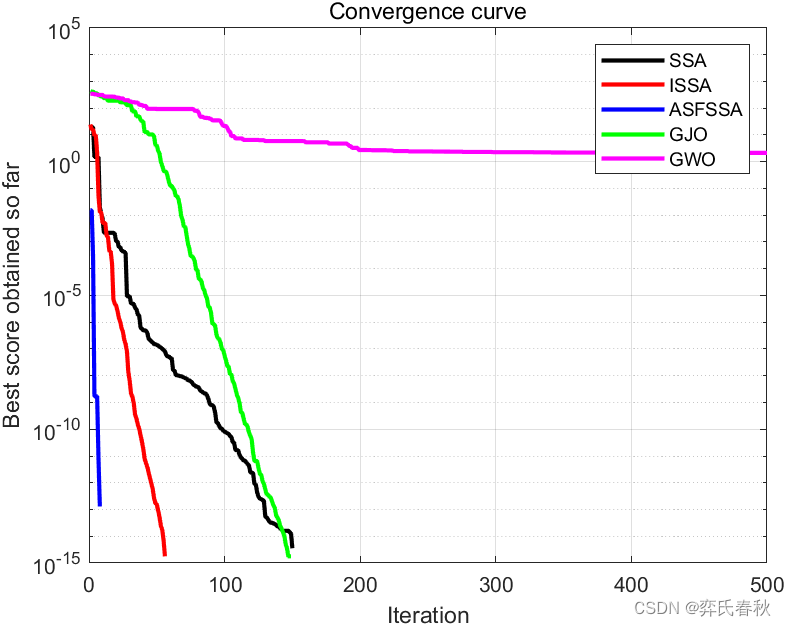
 F12:

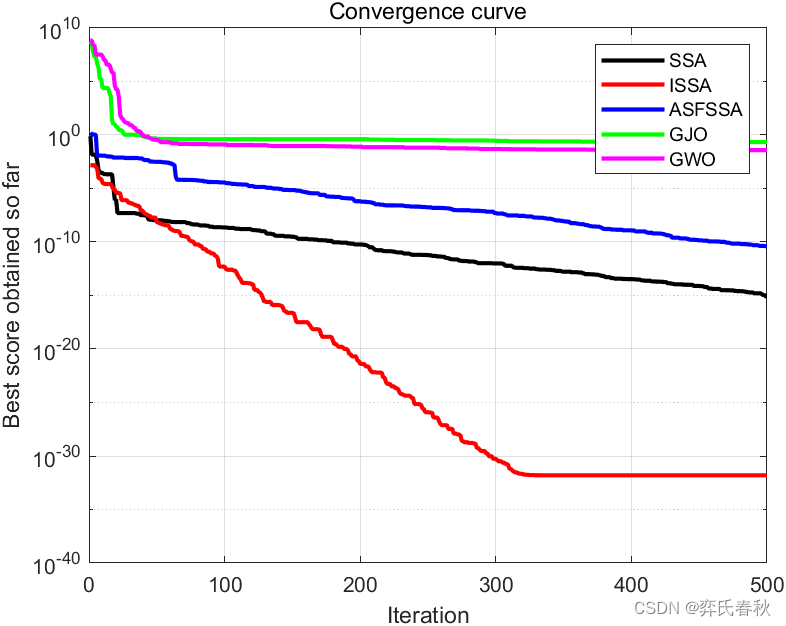
F13:

The best optimal value of the objective funciton found by SSA is : 1.3498e-32
The best optimal value of the objective funciton found by ISSA is : 1.3498e-32
The best optimal value of the objective funciton found by ASFSSA is : 1.8428e-32
The best optimal value of the objective funciton found by GJO is : 0.29653
The best optimal value of the objective funciton found by GWO is : 5.7685e-06

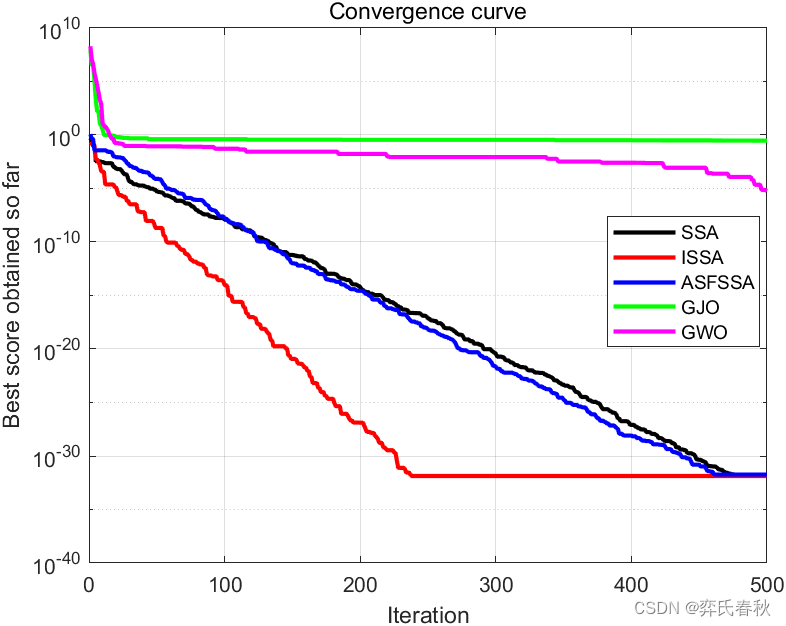
 F21:

The best optimal value of the objective funciton found by SSA is : -5.0552
The best optimal value of the objective funciton found by ISSA is : -10.1532
The best optimal value of the objective funciton found by ASFSSA is : -5.0552
The best optimal value of the objective funciton found by GJO is : -10.1368
The best optimal value of the objective funciton found by GWO is : -5.1002

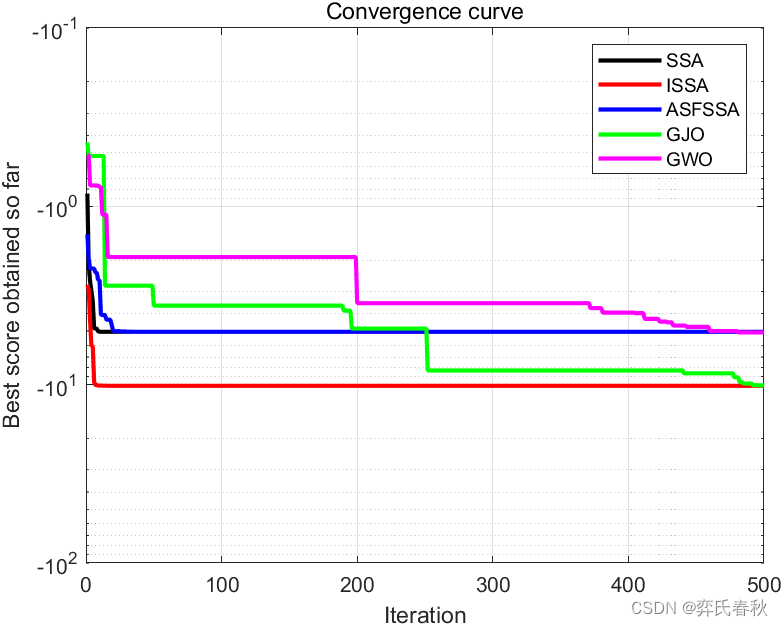
F23:

The best optimal value of the objective funciton found by SSA is : -10.5364
The best optimal value of the objective funciton found by ISSA is : -10.5364
The best optimal value of the objective funciton found by ASFSSA is : -5.1285
The best optimal value of the objective funciton found by GJO is : -10.5253
The best optimal value of the objective funciton found by GWO is : -10.5328

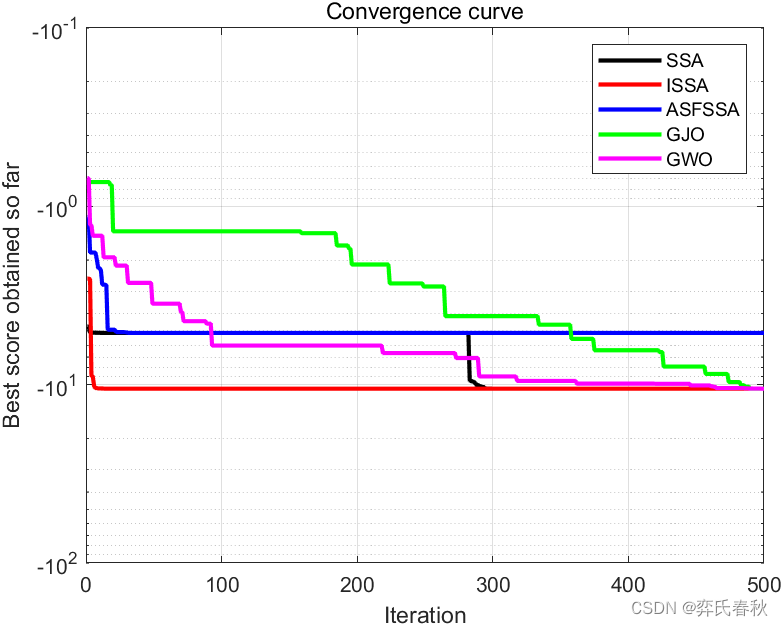
需要代码私信博主