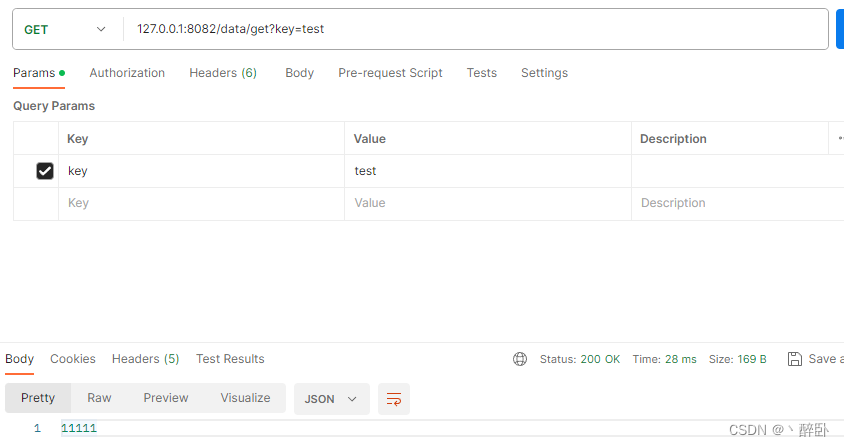
A (codeforces.com)
这题在移动不被挡板挡住以及不超过边界的情况下,每次走的越多那么次数就越少
只要两个每次都走b-a步(已经是不被挡板挡住走的最多了),就不用考虑被挡板挡住的情况,只用单独考虑了,如果可以走b-a,就走b-a,不然就把剩下的走完,只要整除上取整即可
AC代码:
#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int a,b,n;
void solve() {cin>>a>>b>>n;int d=b-a;int x=(n-b)/d+((n-b)%d!=0);int y=(n-a)/d+((n-a)%d!=0);cout<<x+y<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;
// cin>>t;while(t--) {solve();}return 0;
}Problem - M - Codeforces
这题就是问有几个三元组(i,j,k)满足a[j]是a[i]和a[k]的平均数
做法是枚举j和k,然后看前面满足的i有几个
用unordered_map查找的平均时间复杂度是O(1),map查找的时间复杂度是O(logn)
AC代码:
#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=1010;
int a[N];
int n;
void solve() {cin>>n;unordered_map<int,int>mp;for(int i=1;i<=n;i++) cin>>a[i];int res=0;for(int j=1;j<n;j++){for(int k=j+1;k<=n;
k++){res+=mp[2*a[j]-a[k]];}mp[a[j]]++;}cout<<res<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--) {solve();}return 0;
}Problem - I - Codeforces
法一:该题对于每一个柱子,以该柱子为顶点作金字塔,根据几何关系,底面是确定的,然后求最小的能包含所有小底面的大底面,然后根据几何关系确定顶点,由于顶点要求x,y,z是整数,所以大底面边长得是偶数,所以如果是奇数,就得加1
AC代码:
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
int n;
void solve() {cin>>n;int x1=2e9,x2=-2e9,y1=2e9,y2=-2e9;for(int i=0;i<n;i++){int x,y,h;cin>>x>>y>>h;x1=min(x1,x-h);x2=max(x2,x+h);y1=min(y1,y-h);y2=max(y2,y+h);}int h=max((x2-x1)/2+((x2-x1)%2!=0),(y2-y1)/2+((y2-y1)%2!=0));cout<<(x1+x2)/2<<' '<<(y1+y2)/2<<' '<<h<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;
// cin>>t;while(t--) {solve();}return 0;
}法二:
 一共四个面,然后每个面的朝向以及斜率都是固定的,我们只需要考虑对于一根柱子,我们分别让四个面往柱子靠近,刚好能够抵住,这样合成的金字塔是覆盖所有柱子的情况下最小的
一共四个面,然后每个面的朝向以及斜率都是固定的,我们只需要考虑对于一根柱子,我们分别让四个面往柱子靠近,刚好能够抵住,这样合成的金字塔是覆盖所有柱子的情况下最小的
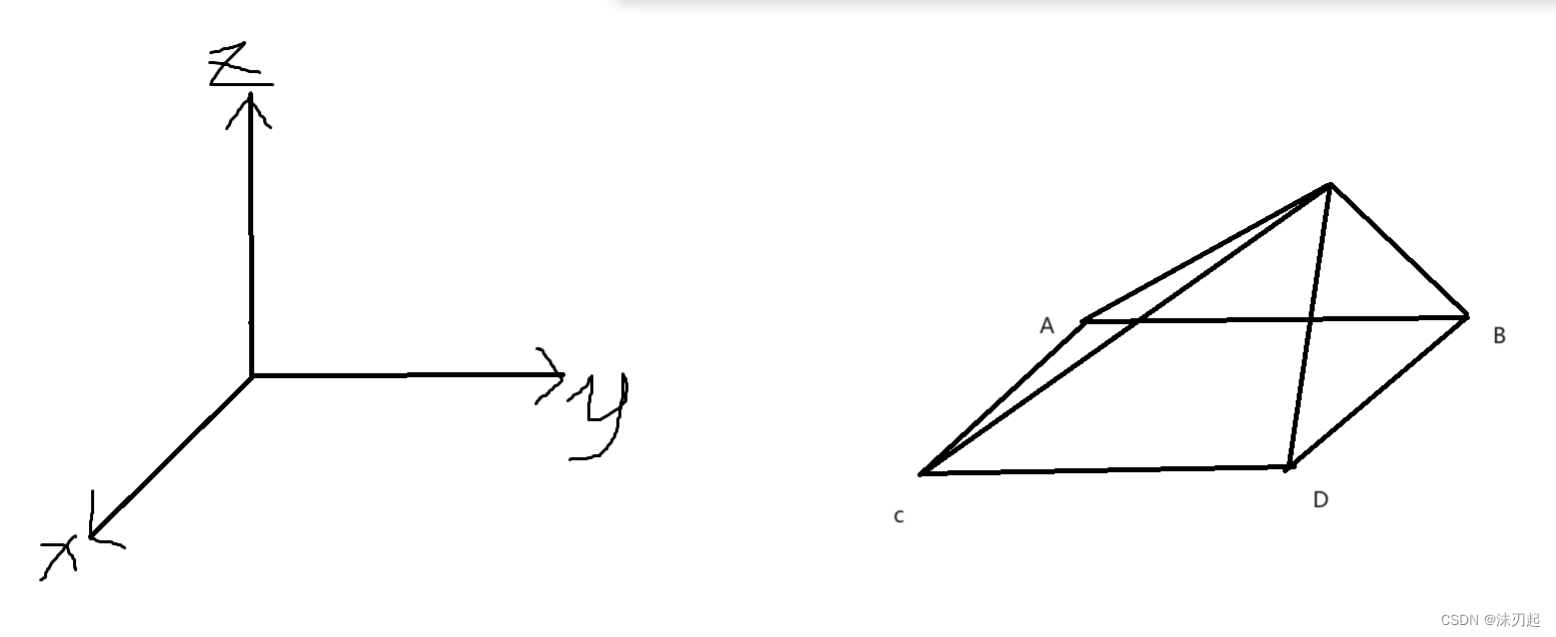
就是刚好让柱子的顶点在这个面上,求出截距,然后取max(截距是在z轴上的截距)
然后两两相邻的面可以与z=0这个面进行联立,得到底面4个交点坐标,从而确定整个底面,如果底面边长为奇数,那么加1(确保顶点坐标为整数),从而确定顶点坐标
AC代码:
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
int n;
struct Point{
public:int x,y;Point(int x1,int y1):x(x1),y(y1){}
};
void solve() {cin>>n;int c1=-2e9,c2=-2e9,c3=-2e9,c4=-2e9;for(int i=0;i<n;i++){int x,y,h;cin>>x>>y>>h;//z=y+c1==>c1=z-yc1=max(c1,h-y);//z=x+c2==>c2=z-xc2=max(c2,h-x);//z=-y+c3==>c3=z+yc3=max(c3,h+y);//z=-x+c4==>c4=z+xc4=max(c4,h+x);}Point A(-c2,-c1),B(-c2,c3),C(c4,c3),D(c4,-c1);int h=max((D.x-A.x)/2+((D.x-A.x)%2!=0),(B.y-A.y)/2+((B.y-A.y)%2!=0));int x=(A.x+D.x)/2;int y=(C.y+D.y)/2;cout<<x<<' '<<y<<' '<<h<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;
// cin>>t;while(t--) {solve();}return 0;
}Problem - E - Codeforces
法一:
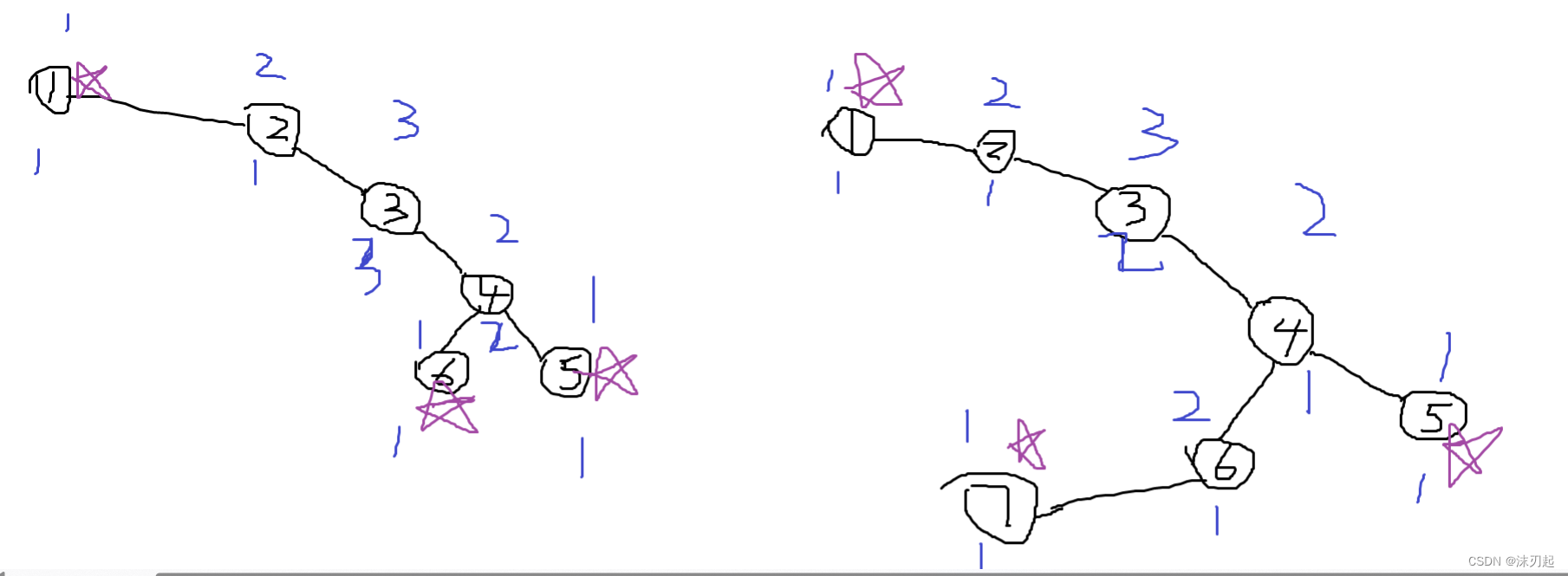
利用bfs一层一层搜,将加粗的所有点入队作为第一层,然后搜下一层,如果第一次搜到就更新距离加1,并且记录到该点为止一共有几个到它距离相同的加粗的点,把该点放入队列中,可以下一次继续拓展下一层,如果搜过了,那么看dist[u]是不是等于dist[v]+1,如果相等,那么可以把到点u距离相同的加粗的点的个数加到点v上
最后枚举每个点,只要有一个点满足到该点的距离相同的加粗的点的个数为m,那么就输出YES,如果一个点也不满足,那么就输出NO
AC代码:
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5+10;
int dist[N];
int cnt[N];
int n,m;
vector<vector<int>>e(N);
void solve() {cin>>n>>m;for(int i=0;i<n-1;i++){int u,v;cin>>u>>v;e[u].push_back(v);e[v].push_back(u);}queue<int>q;for(int i=0;i<m;i++){int x;cin>>x;q.push(x);dist[x]=1;cnt[x]=1;}while(q.size()){int t=q.front();q.pop();for(auto v:e[t]){if(!dist[v]){dist[v]=dist[t]+1;cnt[v]+=cnt[t];q.push(v);}else if(dist[v]==dist[t]+1){cnt[v]+=cnt[t];}}}for(int i=1;i<=n;i++){if(cnt[i]==m){cout<<"YES"<<endl;cout<<i<<endl;return;}}cout<<"NO"<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;
// cin>>t;while(t--) {solve();}return 0;
}法二:
利用树的中心(有专门的模板)
先将那些不可能成为答案的点删掉(从叶子节点一直到加粗的点,将这些点标记,枚举到标记的点的时时候就跳过),这样所有叶子节点就都变成加粗的点了,然后求一遍树的中心,答案只可能在树的中心中(树的中心最多只有两个),因为树的中心到最远的点的距离最近,如果存在一个点满足到所有加粗的点(此时已经变成叶子节点了)的距离相等,那么它肯定是中心
找到中心之后,进行验证是否是答案,只要跑一遍BFS,判断它到所有加粗的点的距离是否相等即可
AC代码:
#include <bits/stdc++.h>
#include <cstdio>
#define endl '\n'
#define int long long
using namespace std;
const int N = 2e5 + 10;
int d1[N], d2[N];
int p1[N];
int up[N];
int du[N];//度数
int dist[N];
bool vis[N];
bool unused[N];
bool teams[N];
int n, m;
vector<vector<int>>e(N);
vector<int>team;
vector<int>zhongdian;
int dfs_d(int u, int fa) {d1[u] = 0; //d1[u]记录从u点向下走的最大长度d2[u] = 0; //d2[u]记录从u点向下走的次大长度for (auto v : e[u]) {if (v == fa || unused[v]) continue; //避免向上搜索int d = dfs_d(v, u) + 1; //从u经ver点往下走的最大长度//p1[u]记录从u点向下走的最长路径是从哪个点下去的if (d >= d1[u]) d2[u] = d1[u], d1[u] = d, p1[u] = v;else if (d > d2[u]) d2[u] = d;}return d1[u];//返回从u点往下走的最大长度
}
void dfs_u(int u, int fa) {for (auto v : e[u]) {if (v == fa || unused[v]) continue; //避免向上搜索//up[ver]记录从ver点向上走的最大长度if (p1[u] == v) up[v] = max(up[u], d2[u]) + 1;else up[v] = max(up[u], d1[u]) + 1;dfs_u(v, u); //深搜u的子节点ver}
}void solve() {cin >> n >> m;for (int i = 0; i < n - 1; i++) {int u, v;cin >> u >> v;e[u].push_back(v);e[v].push_back(u);//度数为1说明是叶子节点du[u]++;du[v]++;}for (int i = 0; i < m; i++) {int x;cin >> x;teams[x] = true; //标记一下teams里的点team.push_back(x);}//把那些没用的点都删掉,使得teams里的点全部成为叶子节点queue<int>q;for (int i = 1; i <= n; i++) {if (du[i] == 1 && !teams[i]) q.push(i);}while (q.size()) {int t = q.front();q.pop();unused[t] = true;for (auto v : e[t]) {if (--du[v] == 1 && !teams[v]) q.push(v);}}int start;//寻找起点,找一个没有被删除的点for (int i = 1; i <= n; i++) {if (!unused[i]) {start = i;break;}}//寻找中点dfs_d(start, -1);dfs_u(start, -1);int res = 2e9;for (int i = 1; i <= n; i++) {if (unused[i]) continue;res = min(res, max(d1[i], up[i]));}for (int i = 1; i <= n; i++) {if (unused[i]) continue;if (max(d1[i], up[i]) == res) zhongdian.push_back(i);}for (auto u : zhongdian) {for (int i = 1; i <= n; i ++) vis[i] = false;queue<int> q;q.push(u);dist[u] = 0;vis[u] = true;bool ok = true;while (q.size()) {int t = q.front();q.pop();for (auto v : e[t]) {if (vis[v] || unused[v]) continue;vis[v] = true;q.push(v);dist[v] = dist[t] + 1;}}for (int i = 1; i < (int)team.size(); i ++)if (dist[team[i - 1]] != dist[team[i]]) {ok = false;break;}if (ok) {cout << "YES" << endl;cout << u << endl;return;}}cout << "NO" << endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t = 1;
// cin>>t;while (t--) {solve();}return 0;
}