重点记忆法
a x 2 + b x + c = 0 ax^2+bx+c=0 ax2+bx+c=0
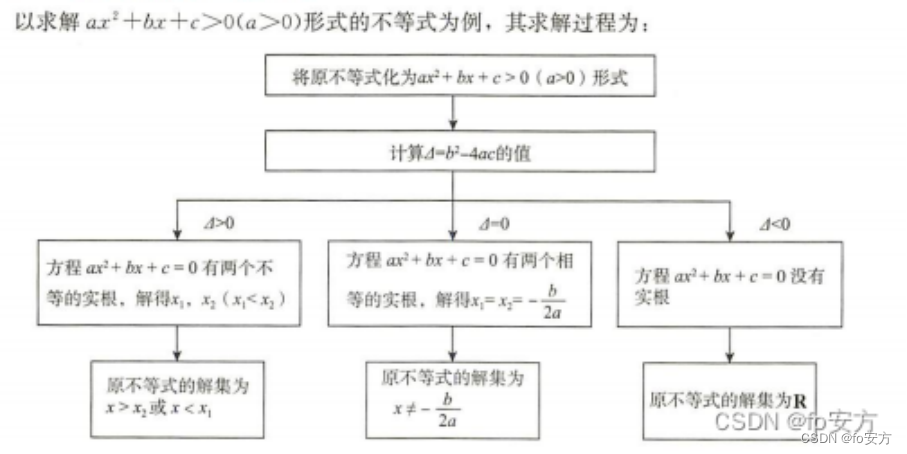
整体可以由: 根(多少,正负,区间) ⟹ \Longrightarrow ⟹ △ △ △ ⟹ \Longrightarrow ⟹ 求根公式 x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△ ⟹ \Longrightarrow ⟹ 韦达定理 ⟹ \Longrightarrow ⟹ 判断两根符号情况,即根多少由 △ △ △判断,根需要求根公式,求根公式可推导韦达定理,韦达定理可判断两根符号情况。
1.根
⟹ \Longrightarrow ⟹ 根的多少: △ △ △>0,方程有两根, x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△,抛物线与x轴有两个交点 ; △ △ △=0,方程有一根, x x x为 − b 2 a -\frac{b}{2a} −2ab,抛物线与x轴有一个交点; △ △ △<0,方程无根,抛物线与x轴没有交点;
⟹ \Longrightarrow ⟹ 根的正负:两正根( △ ≥ 0 , x 1 + x 2 > 0 , x 1 x 2 > 0 △≥0,x_1+x_2>0,x_1x_2>0 △≥0,x1+x2>0,x1x2>0);两负根( △ ≥ 0 , x 1 + x 2 < 0 , x 1 x 2 > 0 △≥0,x_1+x_2<0,x_1x_2>0 △≥0,x1+x2<0,x1x2>0);异号根( x 1 x 2 < 0 x_1x_2<0 x1x2<0)
⟹ \Longrightarrow ⟹ 根的区间:看顶点(横坐标相当于看对称轴,纵坐标相当于看 △ △ △)、看端点(根所分布区问的端点)。or画图+三要素, △ △ △、对称轴和端点代入。
⟹ \Longrightarrow ⟹ 根与系数关系: x 1 + x 2 = − b a x_1+x_2=-\frac{b}{a} x1+x2=−ab, x 1 ⋅ x 2 = c a x_1·x_2=\frac{c}{a} x1⋅x2=ac。
2. △ △ △判别式
⟹ \Longrightarrow ⟹ b 2 − 4 a c b^2-4ac b2−4ac
⟹ \Longrightarrow ⟹ △ △ △>0,方程有两根, x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△,抛物线与x轴有两个交点
⟹ \Longrightarrow ⟹ △ △ △=0,方程有一根, x x x为 − b 2 a -\frac{b}{2a} −2ab,抛物线与x轴有一个交点
⟹ \Longrightarrow ⟹ △ △ △<0,方程无根,抛物线与x轴没有交点
⟹ \Longrightarrow ⟹ y y y的最值为 4 a c − b 2 4 a \frac{4ac-b^2}{4a} 4a4ac−b2 = -△ 4 a \frac{-△}{4a} 4a-△
⟹ \Longrightarrow ⟹ 弦长公式为 △ ∣ a ∣ \frac{\sqrt{△}}{|a|} ∣a∣△
⟹ \Longrightarrow ⟹ 顶点△面积为 ( △ ) 3 8 a 2 \frac{(\sqrt{△})^3}{8a^2} 8a2(△)3
3.求根公式
x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△
⟹ \Longrightarrow ⟹ 韦达定理为 x 1 + x 2 = − b + △ 2 a + − b − △ 2 a = − b a x_1+x_2=\frac{-b+\sqrt{△}}{2a}+\frac{-b-\sqrt{△}}{2a}=-\frac{b}{a} x1+x2=2a−b+△+2a−b−△=−ab
⟹ \Longrightarrow ⟹ 韦达定理为 x 1 ⋅ x 2 = − b + b 2 − 4 a c 2 a ∗ − b − b 2 − 4 a c 2 a = c a x_1·x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}*\frac{-b-\sqrt{b^2-4ac}}{2a}=\frac{c}{a} x1⋅x2=2a−b+b2−4ac∗2a−b−b2−4ac=ac
⟹ \Longrightarrow ⟹ 弦长公式为 ∣ x 1 − x 2 ∣ = ∣ − b + △ 2 a − − b − △ 2 a ∣ = △ ∣ a ∣ |x_1-x_2|=|\frac{-b+\sqrt{△}}{2a}-\frac{-b-\sqrt{△}}{2a}|=\frac{\sqrt{△}}{|a|} ∣x1−x2∣=∣2a−b+△−2a−b−△∣=∣a∣△
⟹ \Longrightarrow ⟹ 顶点△面积为 1 2 ⋅ ∣ y ∣ ⋅ ∣ x 1 − x 2 ∣ = ∣ -△ 4 a ∣ ∗ △ ∣ a ∣ = ( △ ) 3 8 a 2 \frac{1}{2}·|y|·|x_1-x_2|=|\frac{-△}{4a}|*\frac{\sqrt{△}}{|a|}=\frac{(\sqrt{△})^3}{8a^2} 21⋅∣y∣⋅∣x1−x2∣=∣4a-△∣∗∣a∣△=8a2(△)3
4.韦达定理: x 1 + x 2 = − b a x_1+x_2=-\frac{b}{a} x1+x2=−ab, x 1 ⋅ x 2 = c a x_1·x_2=\frac{c}{a} x1⋅x2=ac, ∣ x 1 − x 2 ∣ = b 2 − 4 a c ∣ a ∣ |x_1-x_2|=\frac{\sqrt{b^2-4ac}}{|a|} ∣x1−x2∣=∣a∣b2−4ac
⟹ \Longrightarrow ⟹ 求出关于两个根的对称轮换式的数值
⟹ \Longrightarrow ⟹ 判断两根符号情况
⟹ \Longrightarrow ⟹ 一元三次方程 a x 3 + b x 2 + c x + d = 0 ax^3+bx^2+cx+d=0 ax3+bx2+cx+d=0的韦达定理: x 1 + x 2 + x 3 = − b a x_1+x_2+x_3=-\frac{b}{a} x1+x2+x3=−ab, x 1 x 2 x 3 = − d a x_1x_2x_3=-\frac{d}{a} x1x2x3=−ad, x 1 x 3 + x 2 x 3 + x 1 x 3 = c a x_1x_3+x_2x_3+x_1x_3=\frac{c}{a} x1x3+x2x3+x1x3=ac
⟹ \Longrightarrow ⟹
理解记忆法
求根公式推导
https://www.bilibili.com/read/cv4538376/
韦达定理、弦长公式、顶点△面积推导
韦达定理、弦长公式、顶点△面积由求根公式推导而来
x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△
⟹ \Longrightarrow ⟹ 韦达定理为 x 1 + x 2 = − b + △ 2 a + − b − △ 2 a = − b a x_1+x_2=\frac{-b+\sqrt{△}}{2a}+\frac{-b-\sqrt{△}}{2a}=-\frac{b}{a} x1+x2=2a−b+△+2a−b−△=−ab
⟹ \Longrightarrow ⟹ 韦达定理为 x 1 ⋅ x 2 = − b + b 2 − 4 a c 2 a ∗ − b − b 2 − 4 a c 2 a = c a x_1·x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}*\frac{-b-\sqrt{b^2-4ac}}{2a}=\frac{c}{a} x1⋅x2=2a−b+b2−4ac∗2a−b−b2−4ac=ac
⟹ \Longrightarrow ⟹ 弦长公式为 ∣ x 1 − x 2 ∣ = ∣ − b + △ 2 a − − b − △ 2 a ∣ = △ ∣ a ∣ |x_1-x_2|=|\frac{-b+\sqrt{△}}{2a}-\frac{-b-\sqrt{△}}{2a}|=\frac{\sqrt{△}}{|a|} ∣x1−x2∣=∣2a−b+△−2a−b−△∣=∣a∣△
⟹ \Longrightarrow ⟹ 顶点△面积为 1 2 ⋅ ∣ y ∣ ⋅ ∣ x 1 − x 2 ∣ = ∣ -△ 4 a ∣ ∗ △ ∣ a ∣ = ( △ ) 3 8 a 2 \frac{1}{2}·|y|·|x_1-x_2|=|\frac{-△}{4a}|*\frac{\sqrt{△}}{|a|}=\frac{(\sqrt{△})^3}{8a^2} 21⋅∣y∣⋅∣x1−x2∣=∣4a-△∣∗∣a∣△=8a2(△)3
or
由韦达定理的结论和完全平方公式可推出:
∣ x 1 − x 2 ∣ = ( x 1 + x 2 ) 2 − 4 x 1 x 2 = b 2 − 4 a c ∣ a ∣ |x_1-x_2|=\sqrt{(x_1+x_2)^2-4x_1x_2}=\frac{\sqrt{b^2-4ac}}{|a|} ∣x1−x2∣=(x1+x2)2−4x1x2=∣a∣b2−4ac = △ ∣ a ∣ =\frac{\sqrt{△}}{|a|} =∣a∣△
根的区间之理解
结合图像,就很容易理解了,所以“根的区间判定”,结合图像,是最快的。

以下是其他角度总结,但是缺少图像,不怎么好快速理解:
区问根问题,常使用 “ 两点式 ” 解题法,即看顶点(横坐标相当于看对称轴,纵坐标相当于看 △ △ △)、看端点(根所分布区问的端点)。
为了讨论方便,只讨论 a > 0 a>0 a>0的情况,考试时,若a的符号不定,则需要讨论开口方向。



归类记忆法
根的分布问题:正负根问题和区间根问题


记忆宫殿法
谐音记忆法
求根公式 x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△很重要
快速秒杀法
图形结合法
结合图像,就很容易理解了,所以“根的区间判定”,结合图像,是最快的。
那怎么记忆住这种方式呢
“根的区间”判定:画图+三要素, △ △ △、对称轴和端点代入。
or
根的区间:看顶点(横坐标相当于看对称轴,纵坐标相当于看 △ △ △)、看端点(根所分布区问的端点)。即:遇到根的区间,就联想到横纵坐标,即需要确定横坐标的位置,纵坐标是否存在,但是有这两个还不够,需要第三者加入,即端点代入后的正负,可以决定整个图像的位置。

转图像记忆法
结合字母编码
学习记忆——英语——字母编码
-
求根公式
x 1 , 2 x_{1,2} x1,2= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△,很重要,可以推导出韦达定理等,故事如下:两个苹果(a)上面有个士兵(±),左手拿着香蕉(b)挡住箭(-),右边是一座桥,桥底有一个三角形。

-
一元二次方程的根: x = − b 2 a x=-\frac{b}{2a} x=−2ab:2座桥,桥上有一个香蕉,桥底有两个苹果。
或者:两颗苹果上面有根香蕉,要想托稳香蕉,得有两个横版(一个负号,一个除号)。

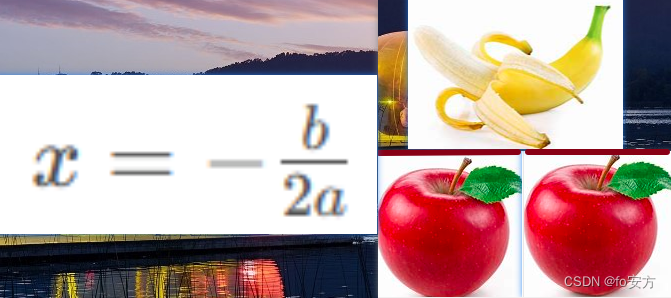
或者两个苹果上面有一座桥和一根香蕉

3. y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c的最值: 4 a c − b 2 4 a \frac{4ac-b^2}{4a} 4a4ac−b2 =— △ 4 a \frac{△}{4a} 4a△
4颗苹果上面有两座桥,桥上有一个三角形。


- 韦达定理
x为剪刀,a苹果,b香蕉,c月亮
剪头➕剪刀可以换,苹果顶着负香蕉
剪刀,剪刀,剪刀,可以换,苹果顶着月亮