二叉树的遍历

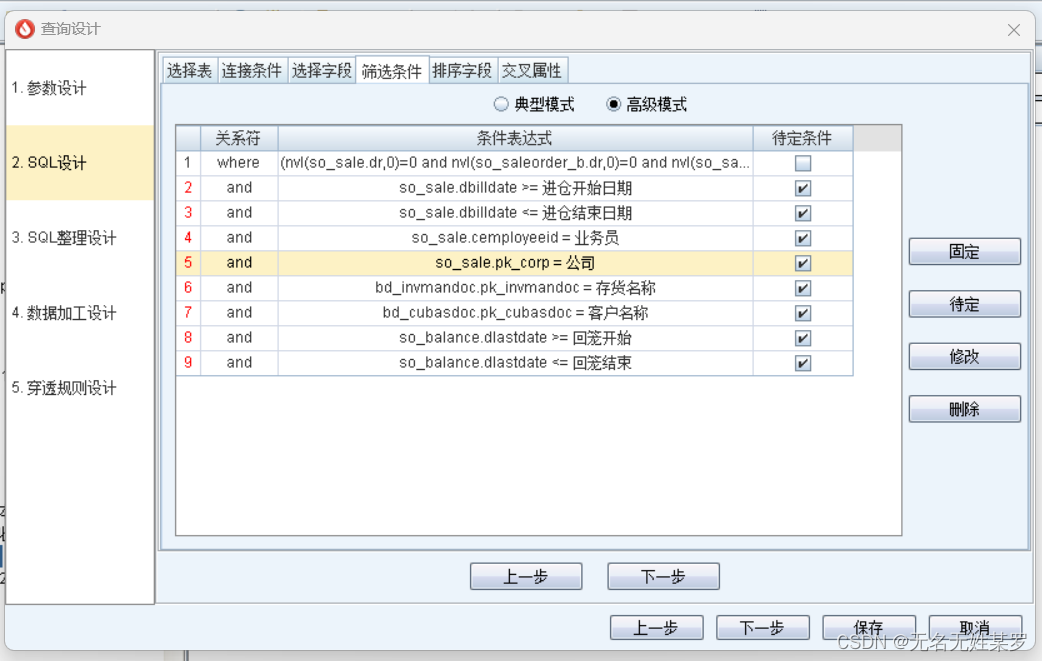
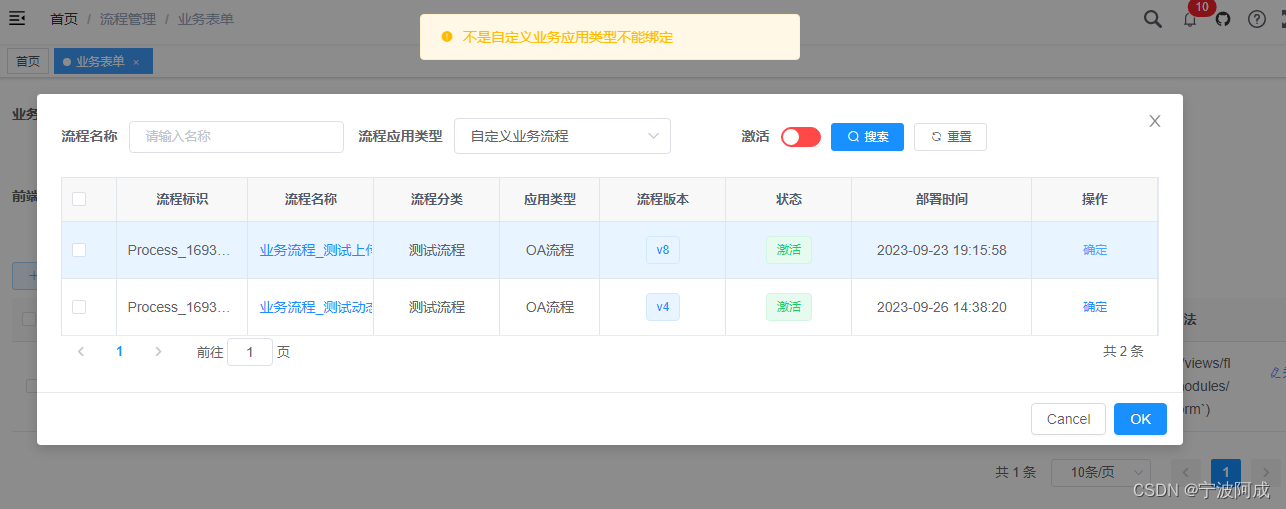
递归实现二叉树的遍历

在遍历的过程中，每个节点都会遍历三次

二叉树的遍历

package binarytree;public class Traverse {public static class Node{public int value;public Node left;public Node right;public Node(int data){this.value = data;}}public static void traverse(Node node) {//每个子树的头节点if (node == null) {return;}//指向左节点traverse(node.left);//从左子树出来回到head节点//指向右节点traverse(node.right);//从右子树出来回到head节点}
}

先序遍历

    //先序遍历public static void traverse_first(Node node) {if (node == null) {return;}System.out.println(node.value + " ");//第一次遍历时输出traverse_first(node.left);traverse_first(node.right);}

中序遍历

    //中序遍历public static void traverse_medium(Node node) {if (node == null) {return;}traverse_medium(node.left);System.out.println(node.value + " ");//第二次遍历时输出traverse_medium(node.right);}

后序遍历

    //后序遍历public static void traverse_later(Node node) {if (node == null) {return;}traverse_later(node.left);traverse_later(node.right);System.out.println(node.value + " ");//第三次遍历时输出}

非递归实现二叉树的遍历

先序遍历

对于每个子树：

头节点入栈 → 节点弹出 → 打印节点 → 右节点 & 左节点入栈

弹出左节点 → 打印左节点 → 进入左子树 → （以左节点为头节点循环）→ 直到左子树的节点全部输出完成

弹出右节点 → 打印右节点 → 进入右子树 → （以右节点为头节点循环）→ 直到右子树的节点全部输出完成

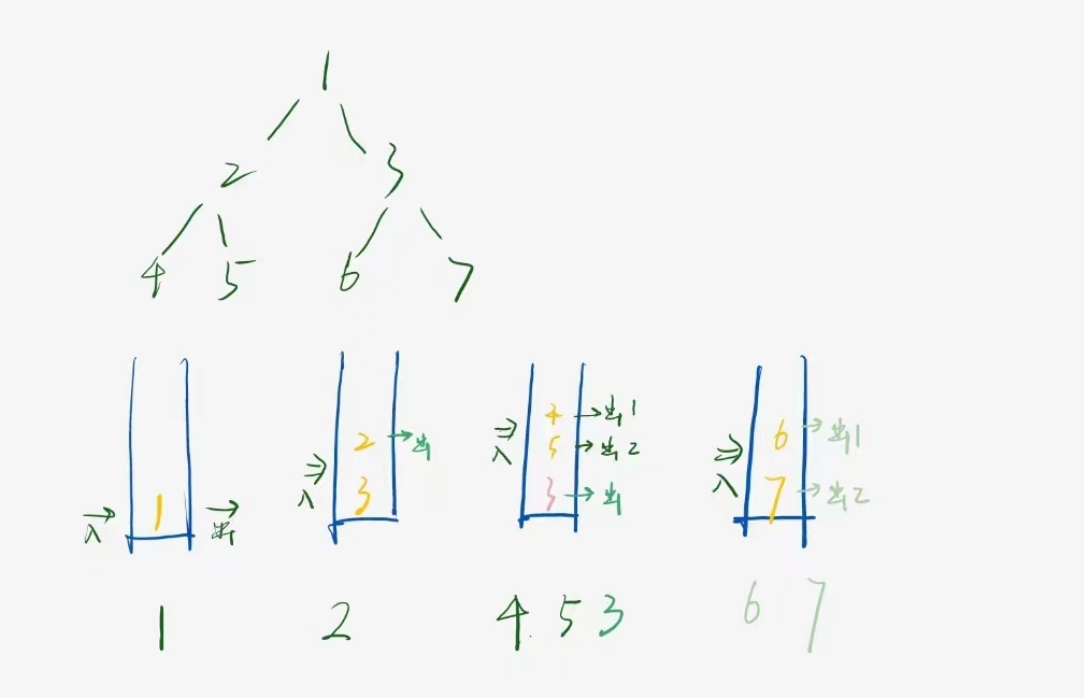
先右再左入栈保证出栈时的顺序是头左右

    //非递归先序遍历public static void traverse_first_nonrecursive(Node node) {if (node == null) {return;}Stack<Node> stack = new Stack<Node>();stack.add(node);while (!stack.isEmpty()) {node = stack.pop();//出栈System.out.println(node + " ");if (node.right != null) {stack.push(node.right);//右节点入栈}if (node.left != null) {stack.push(node.left);//左节点入栈}}}

后序遍历

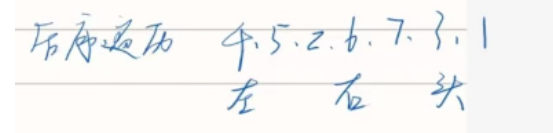
先序遍历压栈时先右节点再左节点，出栈的顺序为头、左、右

如果在压栈是先左节点再右节点，出栈的顺序为头、右、左

将出栈的所有的节点放入另一个栈，出第二个栈的顺序为左、右、头

恰为后序遍历的顺序

    //非递归后序遍历public static void traverse_later_nonrecursive(Node node) {if (node == null) {return;}Stack<Node> stack1 = new Stack<Node>();Stack<Node> stack2 = new Stack<Node>();stack1.push(node);while (!stack1.isEmpty()) {node = stack1.pop();stack2.push(node);//在栈1出栈后压入栈2if (node.left != null) {stack1.push(node.left);//左节点入栈}if (node.right != null) {stack1.push(node.right);//右节点入栈}while (!stack2.isEmpty()) {System.out.println(stack2.pop().value + " ");//栈2弹出}}}

中序遍历

对于每个子树：

整个子树的左子树全部入栈 → 依次弹出

如果弹出的节点无右节点 → 直接打印该节点 → 弹出下一个 → 判断弹出的节点

如果弹出的节点有右节点 → 右节点入栈 → （以右节点为头节点循环）→ 直到右子树的节点全部输出完成 → 弹出下一个

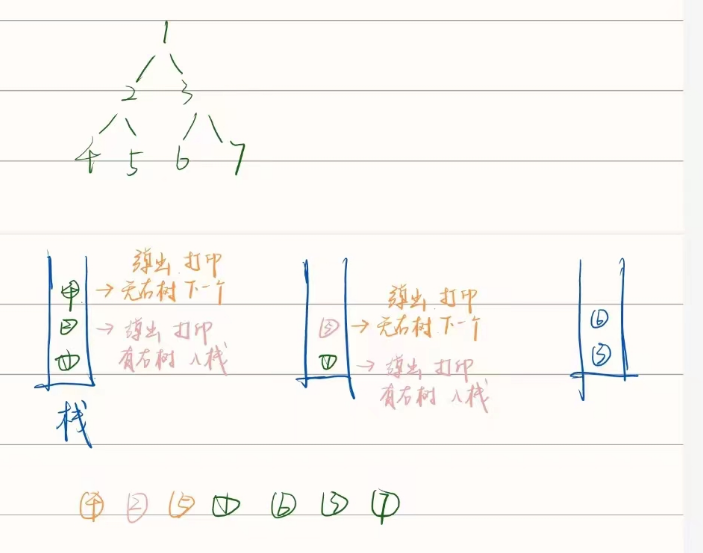
为什么这样遍历输出的顺序就是左、中、右？

入栈时，头 → 左；出栈时，左 → 头

出栈的时候不断判断节点是否有右节点插入右节点

如果在右子树中存在左子树，则继续进行左 → 头的遍历

    //非递归中序遍历public static void traverse_medium_nonrecursive(Node node) {if (node == null) {return;}Stack<Node> stack = new Stack<Node>();while (!stack.isEmpty() && node != null) {if (node != null) {stack.push(node);node = node.left;//整个左子树入栈} else {node = stack.pop();//出栈System.out.println(node.value + " ");node = node.right;//如果右节点为null则弹出下一个，如果不为null则将右节点弹入栈}}}

如何完成二叉树的宽度的优先遍历

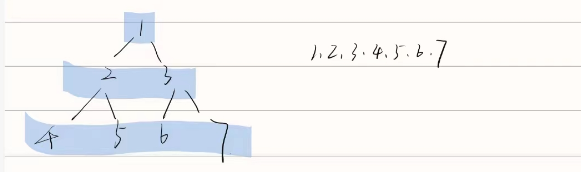
二叉树的深度遍历 = 二叉树的先序遍历

二叉树的宽度遍历：每一层从左到右横向遍历

头节点入队列（先进先出），节点弹出打印，先放左再放右

（类似于先序遍历，栈结构换为队列结构，先右再左换为先左再右）

package binarytree;import java.util.LinkedList;
import java.util.Queue;public class WidthTraversal {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static void widthTraversal(Node node){if(node == null){return;}Queue<Node> queue = new LinkedList<>();queue.add(node);while(!queue.isEmpty()){Node node0 = queue.poll();System.out.println(node0.value);if(node0.left != null){queue.add(node0.left);//先右节点入队列}if(node0.right != null){queue.add(node0.right);//再左节点入队列}}}
}

求一颗二叉树的宽度

1、使用HashMap结构记录某个节点所在的层数，在宽度遍历的时候统计每层的节点个数

几个变量：int thisLevel，当前所在的层数

int thislevelNodes，当前层有多少个节点

int max，最大的层节点数

    //求二叉树的最大宽度public static Integer getmaxWidth(Node node) {if (node == null) {return Integer.MIN_VALUE;}int thislevel = 1;//当前所在的层数int thislevelNodes = 0;//当前层有多少个节点int max = Integer.MIN_VALUE;//最大的层节点数HashMap<Node, Integer> levelMap = new HashMap<>();//HashMap结构存储层数levelMap.put(node, 1);//头节点初始化Queue<Node> queue = new LinkedList<>();queue.add(node);while (!queue.isEmpty()) {Node node0 = queue.poll();if(thislevel == levelMap.get(node0)){thislevelNodes++;//个数++}else{thislevel++;max = Math.max(max,thislevelNodes);//存最大值thislevelNodes = 1;//当一个节点不等于当前节点，此时node0节点已经来到了下一行节点，所以初始值为1}//记录层数if (node0.left != null) {queue.add(node0.left);//先右节点入队列levelMap.put(node0.left, thislevel + 1);//当前节点的左孩子在下一层}if (node0.right != null) {queue.add(node0.right);//再左节点入队列levelMap.put(node0.right, thislevel + 1);//当前节点的右孩子在下一层}}return Math.max(max,thislevelNodes);//最后一行的节点仍需和max比较取较大值}