目录
选择题
1、进制 格式
2、 数组名在&和sizeof后,表数组本身
3、求二维数组某元素地址
编辑 编辑
4、x = x & (x-1) 二进制位1的个数
编辑 5、斐波那契递归次数
编程题
1、计算糖果
2、进制转换
选择题
1、进制 格式


十进制转二进制就除2,转八进制就除8,然后再从后往前写。
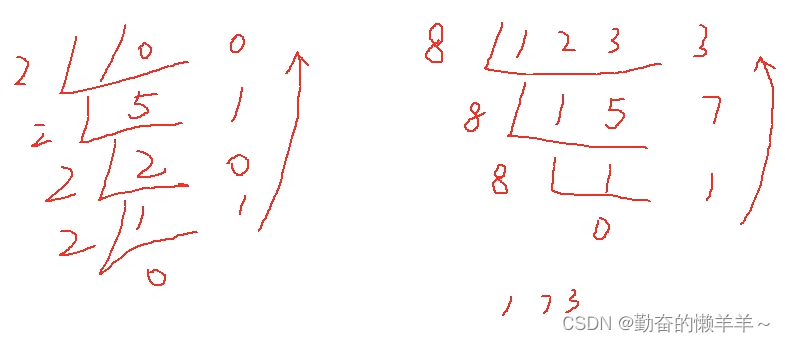
2、 数组名在&和sizeof后,表数组本身

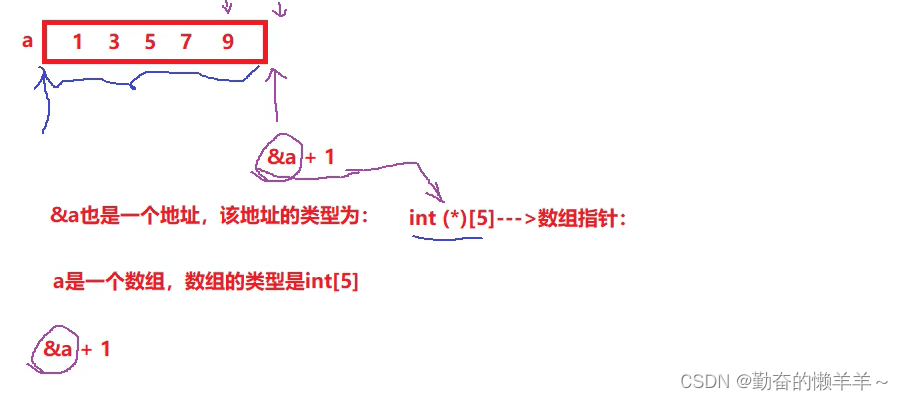
3、求二维数组某元素地址
4、x = x & (x-1) 二进制位1的个数

 5、斐波那契递归次数
5、斐波那契递归次数

编程题
1、计算糖果

1、A - B = a 2、B - C = b 3、A + B = c 4、B + C = d 这道题目的实质是:判断三元一次方程组是否有解及求解, 这里是小学生都会的问题了^^ 1+3可以得到A=(a+c)/2;4-2可以得到C=(d-b)/2;
2+4可以得到B2=(b+d)/2,3-1可以得到B1=(c-a)/2;
如果B1不等B2则表达式无解
#include<iostream>
using namespace std;
int main()
{int a,b,c,d;cin>>a>>b>>c>>d;int A=(a+c)/2;int C=(d-b)/2;int B1=(c-a)/2;int B2=(b+d)/2;if(B1!=B2)cout<<"No";elsecout<<A<<" "<<B1<<" "<<C;return 0;
}2、进制转换

#include <cstdarg>
#include <iostream>
#include<string>
#include<algorithm>
using namespace std;
int main() {string s, table = "0123456789ABCDEF";int m, n;cin >> m >> n;if(m==0)cout << m;bool flag = false;
// 如果是负数,则转成正数,并标记一下if (m < 0) {m = 0 - m;flag = true;}
// 按进制换算成对应的字符添加到swhile (m) {s += table[m % n];m /= n;}if (flag)s += '-';reverse(s.begin(), s.end());cout << s << endl;return 0;
}
// 64 位输出请用 printf("%lld")