目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
5.算法完整程序工程
1.算法运行效果图预览

2.算法运行软件版本
matlab2022a
3.部分核心程序
...................................................................
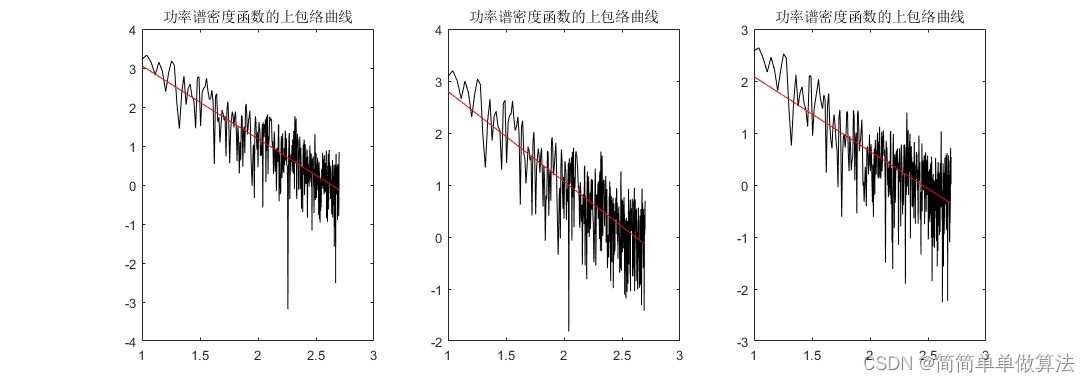
%通过功率谱密度曲线初步得到斜率
figure;
y_envelope0 = log10(ya0(t));
t_envelope0 = log10(t);
subplot(131);plot(t_envelope0,y_envelope0,'k'); title('功率谱密度函数的上包络曲线');
hold on;
%进行线性拟合
Func_coff0=polyfit(t_envelope0,y_envelope0,1);
plot(t_envelope0,Func_coff0(1)*t_envelope0+Func_coff0(2),'r');
r0 = -Func_coff0(1);y_envelope1 = log10(ya1(t));
t_envelope1 = log10(t);
subplot(132);plot(t_envelope1,y_envelope1,'k'); title('功率谱密度函数的上包络曲线');
hold on;
%进行线性拟合
Func_coff1=polyfit(t_envelope1,y_envelope1,1);
plot(t_envelope1,Func_coff1(1)*t_envelope1+Func_coff1(2),'r');
r1 = -Func_coff1(1);y_envelope2 = log10(ya2(t));
t_envelope2 = log10(t);
subplot(133);plot(t_envelope2,y_envelope2,'k'); title('功率谱密度函数的上包络曲线');
hold on;
%进行线性拟合
Func_coff2=polyfit(t_envelope2,y_envelope2,1);
plot(t_envelope2,Func_coff2(1)*t_envelope2+Func_coff2(2),'r');
r2 = -Func_coff2(1);
r = [r0 r1 r2];
disp(' 原始信号r -10db噪声的r -20db噪声的r');
r%下面用论文中的小波算法求解r指数,调用自定义小波计算函数
figure;
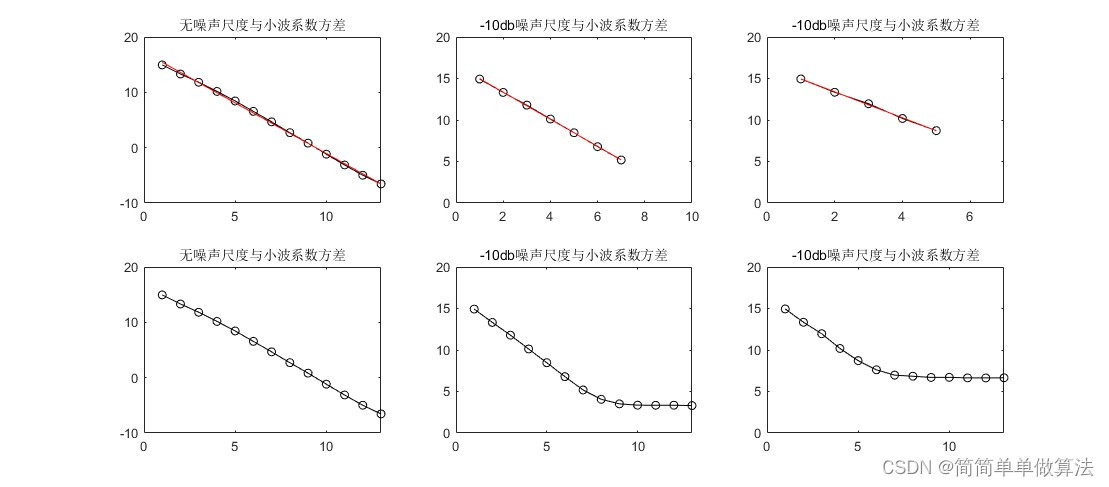
[cdv0,tt0,coffs0] = func_wavelet_calculate(signal,13,1);subplot(231);
plot(tt0,cdv0,'k-o');hold on;
coff0=polyfit(tt0,cdv0,1);
plot(tt0,coff0(1)*tt0+coff0(2),'r'); title('无噪声尺度与小波系数方差');
rr0 = -coff0(1);
delta0 = coff0(2);
axis([0,13,-10,20]);
subplot(234);
plot(tt0,cdv0,'k-o');title('无噪声尺度与小波系数方差');hold off;
axis([0,13,-10,20]);[cdv1,tt1,coffs1] = func_wavelet_calculate(signal_10db,13,1);subplot(232);
plot(tt1(1:7),cdv1(1:7),'k-o');hold on;
coff1=polyfit(tt1(1:7),cdv1(1:7),1);
plot(tt1(1:7),coff1(1)*tt1(1:7)+coff1(2),'r'); title('-10db噪声尺度与小波系数方差');
rr1 = -coff1(1);
delta1 = coff1(2);
axis([0,10,0,20]);
subplot(235);
plot(tt1,cdv1,'k-o');title('-10db噪声尺度与小波系数方差');
axis([0,13,0,20]);[cof_new1,signal11] = func_dewavelet_calculate(signal_10db,rr1,delta1,-10,coffs1,13);[cdv2,tt2,coffs2] = func_wavelet_calculate(signal_20db,13,1);
subplot(233);
plot(tt2(1:5),cdv2(1:5),'k-o');hold on;
coff2=polyfit(tt2(1:5),cdv2(1:5),1);
plot(tt2(1:5),coff2(1)*tt2(1:5)+coff2(2),'r'); title('-10db噪声尺度与小波系数方差');
rr2 = -coff2(1);
delta2 = coff2(2);
axis([0,7,0,20]);
subplot(236);
plot(tt2,cdv2,'k-o');title('-10db噪声尺度与小波系数方差');
axis([0,13,0,20]);[cof_new2,signal22] = func_dewavelet_calculate(signal_20db,rr2,delta2,-20,coffs2,13);rr =[rr0 rr1 rr2];
disp(' 原始信号r -10db噪声的r -20db噪声的r');
rrfigure
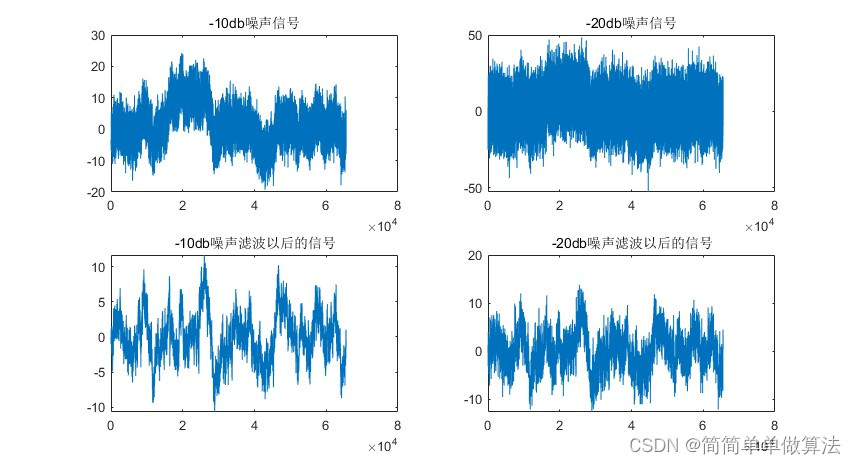
subplot(221);plot(signal_10db);title('-10db噪声信号');
subplot(223);plot(signal11); title('-10db噪声滤波以后的信号');subplot(222);plot(signal_20db);title('-20db噪声信号');
subplot(224);plot(signal22); title('-20db噪声滤波以后的信号');clear Func_coff0 Func_coff1 Func_coff2 a0 a1 a2 b0 b1 b2 cdv0 cdv1 cdv2 coff0 coff1 coff2
clear powera0 powera1 powera2 r r0 r1 r2 rr0 rr1 rr2 t t_envelope0 t_envelope1 t_envelope2 tt0 tt1 tt2 ya0 ya1 ya2
clear y_envelope0 y_envelope1 y_envelope2
17_002m4.算法理论概述
基于小波变换的分形信号r指数求解算法是一种利用小波变换和分形理论对信号进行分析的方法。下面将详细介绍这种算法的原理和数学公式。
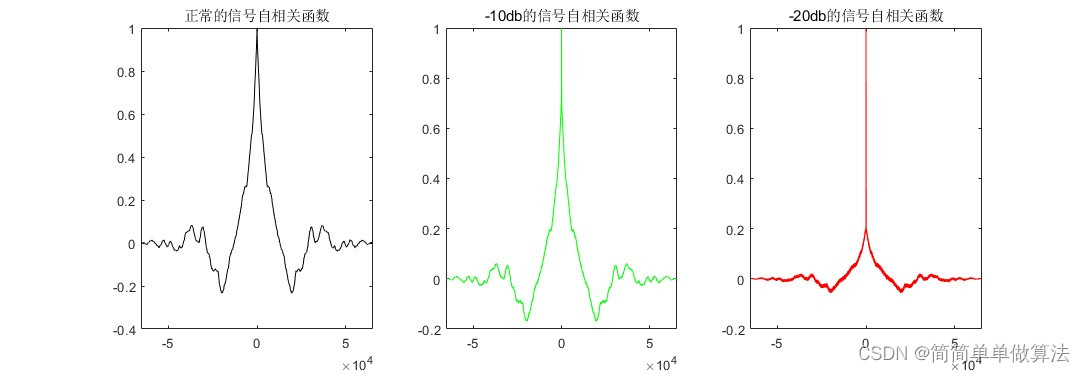
分形信号是一种具有自相似性的非周期信号,其局部和整体具有相似的特征。在分形信号的分析中,r指数是一个重要的参数,用于描述信号的奇异性和不规则性。r指数越大,表示信号越不规则,奇异性越强。
小波变换是一种时频分析方法,能够将信号分解成不同尺度的成分,并对每个成分进行分析。基于小波变换的分形信号r指数求解算法利用小波变换对信号进行多尺度分解,提取出信号在不同尺度下的特征,然后利用分形理论对这些特征进行分析,计算出信号的r指数。
具体地,基于小波变换的分形信号r指数求解算法可以分为以下几个步骤:
- 对信号进行小波变换,得到一系列小波系数。
- 对每个尺度下的小波系数进行统计分析,计算出该尺度下的分形维数。
- 对所有尺度下的分形维数进行拟合,得到信号的r指数。
基于小波变换的分形信号r指数求解算法的数学公式主要包括以下几个部分:
小波变换
对信号f(t)进行小波变换,可以得到一系列小波系数Wf(a,b),其中a表示尺度参数,b表示平移参数。小波变换的数学公式可以表示为:
Wf(a,b)=1a∫f(t)ψ∗(t−ba)dtWf(a,b) = \frac{1}{\sqrt{a}} \int f(t) \psi^*(\frac{t-b}{a}) dtWf(a,b)=a1∫f(t)ψ∗(at−b)dt
其中,ψ(t)是小波基函数,ψ∗(t)是其共轭复数。
分形维数计算
对每个尺度下的小波系数进行统计分析,可以计算出该尺度下的分形维数。具体地,可以使用盒计数法或功率谱法等方法进行计算。以盒计数法为例,假设将小波系数分成N个盒子,每个盒子的长度为ε,则分形维数D可以用以下公式表示:
D=limε→0logN(ε)log(1/ε)D = \lim_{\varepsilon \to 0} \frac{\log N(\varepsilon)}{\log (1/\varepsilon)}D=limε→0log(1/ε)logN(ε)
其中,N(ε)表示盒子数量。
r指数计算
对所有尺度下的分形维数进行拟合,可以得到信号的r指数。具体地,可以使用最小二乘法等方法进行拟合。以最小二乘法为例,假设分形维数D与尺度参数a之间存在以下关系:
D=Da+rDaD = D_a + r D_aD=Da+rDa
其中,Da表示信号的平均分形维数,r表示信号的r指数。则可以通过最小二乘法拟合出r的值。
需要注意的是,基于小波变换的分形信号r指数求解算法的具体实现可能会因小波基函数的选择、尺度参数的选取等因素而有所不同。此外,该算法的计算复杂度较高,需要较大的计算资源和时间。
5.算法完整程序工程
OOOOO
OOO
O